Quadratic forms for surgery
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Let 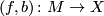 be a degree one normal map from a manifold of dimension
be a degree one normal map from a manifold of dimension 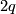 . Then the surgery kernel of
. Then the surgery kernel of 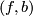 ,
, 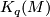 , comes equipped with a subtle and crucial quadratic refinement. This page describes both the algebraic and geometric aspects of such quadratic refinements
, comes equipped with a subtle and crucial quadratic refinement. This page describes both the algebraic and geometric aspects of such quadratic refinements
2 Topology
Let $$(f,b)\: M \to X$$ be a $q$-connected normal map, $m =2q$, $q$ odd and $q \ge 3$. Assume also $X$ is $1$-connected. Let $$I_q(M)$$ be the set of regular homotopy classes of immersions $S^q \to M$ which represent elements of the surgery kernel $K_q(M)$ (with respect to the homomorphism $I_q(M) \to K_q(M)$. It is an abelian group. We have two invariants: \roster \item $\mu =$ double point obstruction $I_q(M) \to \Bbb Z_2$ \item $\Cal O =$ Browder's framing obstruction $I_q(M) \to \Bbb Z_2$ \endroster \proclaim{Claim} The function $$ \mu' := \mu + \Cal O\: I_q(M) \to \Bbb Z_2 $$ is homotopy invariant (i.e., if $a,b\: S^q \to M$ are immersions representing the same element $x \in K_q(M)$, then $\mu'(a) = \mu'(b)$). \endproclaim \demo{Proof} The homomorphism $I_q(M) \to K_q(M)$ is onto and two-to-one. The distinct elements over a given $x \in K_q(M)$ are detected by Browder's framing obstruction $\Cal O \in \pi_{q}(\text{O}/\text{O}_q) = \Bbb Z_2$ (this uses Smale-Hirsch theory). Let $a$ and $b$ be these immersions. Then $a$ and $b$ are not regularly homotopic. (Note: when $q\ne 3,7$ the normal bundles of $a$ and $b$ are distinct; when $q=3,7$ they are both trivial.) We can assume without loss in generality that $\Cal O(a) = 0$ (so $\Cal O(b) =1$). Then $a$ is a framed immersion. \medskip \noindent {\sl Case 1:} $\mu(a) = 0$. \medskip If $\mu(a) = 0 $ then a result of Whitney (the ``Whitney trick) shows that $a$ is regularly homotopic to a (framed) embedding, so assume that $a$ is a framed embedding. Whitney's method of introducing a single double point to $a$ in a coordinate chart yields a new immersion $b'$ such that $b'$ has one double point and $b'$ still represents $x$. Then $\mu(b') = 1$, so $b'$ isn't regularly homotopic to $a$. It must therefore be regularly homotopic to $b$. Hence $\mu(b) = 1$. It follows that $\mu'(a) = \mu'(b)$ in this case. \medskip \noindent {\sl Case 2:} $\mu(a) = 1$. \medskip In this case $a$ is regularly homotopic to an immersion with exactly one double point. By introducing another double point we get a $b$ representing $x$ such that $\mu(b) = 0$. Then $b$ is not regularly homotopic to $a$ so it must be regularly homotopic to $b$. Consequently, $\mu(b) = 0$. Therefore $\mu'(a) = \mu'(b)$ in this case.\qed \enddemo Let $$E_q(M) $$ be the isotopy classes of embeddings $S^q \to M$ representing elements of $K_q(M)$. Then we have a function $E_q(M) \to I_q(M)$. \proclaim{Corollary} The function $\Cal O\: E_q(M) \to \Bbb Z_2$ is homotopy invariant, i.e., it factors through $K_q(M)$. \endproclaim
3 Algebra
4 References
$-connected. Let $$I_q(M)$$ be the set of regular homotopy classes of immersions $S^q \to M$ which represent elements of the surgery kernel $K_q(M)$ (with respect to the homomorphism $I_q(M) \to K_q(M)$. It is an abelian group. We have two invariants: \roster \item $\mu =$ double point obstruction $I_q(M) \to \Bbb Z_2$ \item $\Cal O =$ Browder's framing obstruction $I_q(M) \to \Bbb Z_2$ \endroster \proclaim{Claim} The function $$ \mu' := \mu + \Cal O\: I_q(M) \to \Bbb Z_2 $$ is homotopy invariant (i.e., if $a,b\: S^q \to M$ are immersions representing the same element $x \in K_q(M)$, then $\mu'(a) = \mu'(b)$). \endproclaim \demo{Proof} The homomorphism $I_q(M) \to K_q(M)$ is onto and two-to-one. The distinct elements over a given $x \in K_q(M)$ are detected by Browder's framing obstruction $\Cal O \in \pi_{q}(\text{O}/\text{O}_q) = \Bbb Z_2$ (this uses Smale-Hirsch theory). Let $a$ and $b$ be these immersions. Then $a$ and $b$ are not regularly homotopic. (Note: when $q\ne 3,7$ the normal bundles of $a$ and $b$ are distinct; when $q=3,7$ they are both trivial.) We can assume without loss in generality that $\Cal O(a) = 0$ (so $\Cal O(b) =1$). Then $a$ is a framed immersion. \medskip \noindent {\sl Case 1:} $\mu(a) = 0$. \medskip If $\mu(a) = 0 $ then a result of Whitney (the ``Whitney trick'') shows that $a$ is regularly homotopic to a (framed) embedding, so assume that $a$ is a framed embedding. Whitney's method of introducing a single double point to $a$ in a coordinate chart yields a new immersion $b'$ such that $b'$ has one double point and $b'$ still represents $x$. Then $\mu(b') = 1$, so $b'$ isn't regularly homotopic to $a$. It must therefore be regularly homotopic to $b$. Hence $\mu(b) = 1$. It follows that $\mu'(a) = \mu'(b)$ in this case. \medskip \noindent {\sl Case 2:} $\mu(a) = 1$. \medskip In this case $a$ is regularly homotopic to an immersion with exactly one double point. By introducing another double point we get a $b''$ representing $x$ such that $\mu(b'') = 0$. Then $b''$ is not regularly homotopic to $a$ so it must be regularly homotopic to $b$. Consequently, $\mu(b) = 0$. Therefore $\mu'(a) = \mu'(b)$ in this case.\qed \enddemo Let $$E_q(M) $$ be the isotopy classes of embeddings $S^q \to M$ representing elements of $K_q(M)$. Then we have a function $E_q(M) \to I_q(M)$. \proclaim{Corollary} The function $\Cal O\: E_q(M) \to \Bbb Z_2$ is homotopy invariant, i.e., it factors through $K_q(M)$. \endproclaim == Algebra == == References == {{#RefList:}} [[Category:Theory]](f, b) \colon M \to X be a degree one normal map from a manifold of dimension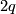 . Then the surgery kernel of
. Then the surgery kernel of 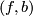 ,
, 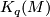 , comes equipped with a subtle and crucial quadratic refinement. This page describes both the algebraic and geometric aspects of such quadratic refinements
, comes equipped with a subtle and crucial quadratic refinement. This page describes both the algebraic and geometric aspects of such quadratic refinements
2 Topology
Let $$(f,b)\: M \to X$$ be a $q$-connected normal map, $m =2q$, $q$ odd and $q \ge 3$. Assume also $X$ is $1$-connected. Let $$I_q(M)$$ be the set of regular homotopy classes of immersions $S^q \to M$ which represent elements of the surgery kernel $K_q(M)$ (with respect to the homomorphism $I_q(M) \to K_q(M)$. It is an abelian group. We have two invariants: \roster \item $\mu =$ double point obstruction $I_q(M) \to \Bbb Z_2$ \item $\Cal O =$ Browder's framing obstruction $I_q(M) \to \Bbb Z_2$ \endroster \proclaim{Claim} The function $$ \mu' := \mu + \Cal O\: I_q(M) \to \Bbb Z_2 $$ is homotopy invariant (i.e., if $a,b\: S^q \to M$ are immersions representing the same element $x \in K_q(M)$, then $\mu'(a) = \mu'(b)$). \endproclaim \demo{Proof} The homomorphism $I_q(M) \to K_q(M)$ is onto and two-to-one. The distinct elements over a given $x \in K_q(M)$ are detected by Browder's framing obstruction $\Cal O \in \pi_{q}(\text{O}/\text{O}_q) = \Bbb Z_2$ (this uses Smale-Hirsch theory). Let $a$ and $b$ be these immersions. Then $a$ and $b$ are not regularly homotopic. (Note: when $q\ne 3,7$ the normal bundles of $a$ and $b$ are distinct; when $q=3,7$ they are both trivial.) We can assume without loss in generality that $\Cal O(a) = 0$ (so $\Cal O(b) =1$). Then $a$ is a framed immersion. \medskip \noindent {\sl Case 1:} $\mu(a) = 0$. \medskip If $\mu(a) = 0 $ then a result of Whitney (the ``Whitney trick) shows that $a$ is regularly homotopic to a (framed) embedding, so assume that $a$ is a framed embedding. Whitney's method of introducing a single double point to $a$ in a coordinate chart yields a new immersion $b'$ such that $b'$ has one double point and $b'$ still represents $x$. Then $\mu(b') = 1$, so $b'$ isn't regularly homotopic to $a$. It must therefore be regularly homotopic to $b$. Hence $\mu(b) = 1$. It follows that $\mu'(a) = \mu'(b)$ in this case. \medskip \noindent {\sl Case 2:} $\mu(a) = 1$. \medskip In this case $a$ is regularly homotopic to an immersion with exactly one double point. By introducing another double point we get a $b$ representing $x$ such that $\mu(b) = 0$. Then $b$ is not regularly homotopic to $a$ so it must be regularly homotopic to $b$. Consequently, $\mu(b) = 0$. Therefore $\mu'(a) = \mu'(b)$ in this case.\qed \enddemo Let $$E_q(M) $$ be the isotopy classes of embeddings $S^q \to M$ representing elements of $K_q(M)$. Then we have a function $E_q(M) \to I_q(M)$. \proclaim{Corollary} The function $\Cal O\: E_q(M) \to \Bbb Z_2$ is homotopy invariant, i.e., it factors through $K_q(M)$. \endproclaim