Principal bundle of smooth manifolds
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Definition
A  -principal bundle for a Lie group
-principal bundle for a Lie group  is a smooth bundle
is a smooth bundle
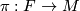 where
where  acts on
acts on  from the right, the action is
free (that is [
from the right, the action is
free (that is [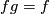 for some
for some
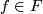
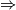
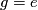 ]), and the
]), and the  -orbits are the fibres,
-orbits are the fibres,
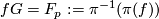 for
every
for
every 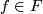 . Then the mapping
. Then the mapping 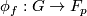 ,
, 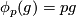 is a diffeomorphism which is equivariant with respect to the action
of
is a diffeomorphism which is equivariant with respect to the action
of  on itself by right translations. The tangent space of the fibre,
on itself by right translations. The tangent space of the fibre,
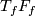 is called the vertical space; by means of the differential
is called the vertical space; by means of the differential
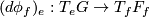 it can be identified with the Lie algebra
it can be identified with the Lie algebra
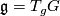 . The vertical spaces together form an integrable distribution
. The vertical spaces together form an integrable distribution
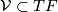 on
on  , the vertical distribution.
, the vertical distribution.
If 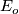 is any
is any  -space, i.e. a manifold on which
-space, i.e. a manifold on which  acts from the left,
we have a free
acts from the left,
we have a free  -action on
-action on 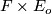 given by
given by 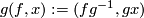 .
Then the orbit space
.
Then the orbit space 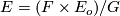 is a bundle over
is a bundle over  with fibres
diffeomorphic to
with fibres
diffeomorphic to 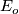 ; it is called an associated bundle to the
principal bundle
; it is called an associated bundle to the
principal bundle  .
In particular, if
.
In particular, if 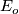 is a vector space and the
is a vector space and the  -action on
-action on 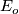 is linear
(a representation of
is linear
(a representation of  ),
then
),
then  is a vector bundle over
is a vector bundle over  , associated to the principal bundle
, associated to the principal bundle  .
.