Petrie conjecture
| Line 3: | Line 3: | ||
The Petrie conjecture was formulated in the following context: suppose that a Lie group $G$ acts smoothly on a closed smooth manifold $M$, what constraints does this place on the topology of $M$ in general and on the Pontrjagin classes of $M$ in particular. | The Petrie conjecture was formulated in the following context: suppose that a Lie group $G$ acts smoothly on a closed smooth manifold $M$, what constraints does this place on the topology of $M$ in general and on the Pontrjagin classes of $M$ in particular. | ||
| − | Petrie restricted his attention to smooth actions of the Lie group $S^1$, i.e., the circle {{cite|Petrie1972}} (or more generally, the torus $T^ | + | Petrie restricted his attention to smooth actions of the Lie group $S^1$, i.e., the circle {{cite|Petrie1972}} (or more generally, the torus $T^k$ for $k \geq 1$ {{cite|Petrie1973}}) |
on closed smooth manifolds $M$ which are [[Fake complex projective spaces|homotopy equivalent to $\CP^n$]]. He has formulated the following conjecture. | on closed smooth manifolds $M$ which are [[Fake complex projective spaces|homotopy equivalent to $\CP^n$]]. He has formulated the following conjecture. | ||
| Line 13: | Line 13: | ||
by the work of {{cite|Dejter1976}} and {{cite|James1985}}. | by the work of {{cite|Dejter1976}} and {{cite|James1985}}. | ||
According to {{cite|Hattori1978}}, the same is true if $M$ admits an invarint almost | According to {{cite|Hattori1978}}, the same is true if $M$ admits an invarint almost | ||
| − | complex structure with the appropriate first Chern class. Another special cases where the Petrie conjecture holds are described by {{cite| | + | complex structure with the appropriate first Chern class. Another special cases where the Petrie conjecture holds are described by {{cite|Wang1975}}, |
| − | + | {{cite|Yoshida1976}}, {{cite|Iberkleid1978}}, {{cite|Muslin1978}}, {{cite|Tsukada&Washiyama1979}}, {{cite|Masuda1981}}, {{cite|Dessai2002}}, and {{cite|Dessai&Wilking2004}}. | |
| − | and {{cite|Dessai&Wilking2004}}. | + | |
== References == | == References == | ||
Revision as of 01:37, 1 December 2010
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Introduction
The Petrie conjecture was formulated in the following context: suppose that a Lie group  acts smoothly on a closed smooth manifold
acts smoothly on a closed smooth manifold  , what constraints does this place on the topology of
, what constraints does this place on the topology of  in general and on the Pontrjagin classes of
in general and on the Pontrjagin classes of  in particular.
in particular.
Petrie restricted his attention to smooth actions of the Lie group  , i.e., the circle [Petrie1972] (or more generally, the torus
, i.e., the circle [Petrie1972] (or more generally, the torus 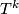 for
for 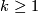 [Petrie1973])
on closed smooth manifolds
[Petrie1973])
on closed smooth manifolds  which are homotopy equivalent to
which are homotopy equivalent to 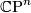 . He has formulated the following conjecture.
. He has formulated the following conjecture.
Conjecture 0.1 [Petrie1972].
Suppose that is a closed smooth manifold homotopy equivalent to
is a closed smooth manifold homotopy equivalent to 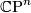 and that
and that  acts smoothly and non-trivially on
acts smoothly and non-trivially on  . Then the total Pontrjagin class
. Then the total Pontrjagin class 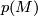 of
of  agrees with that of
agrees with that of 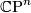 , i.e., for a generator
, i.e., for a generator 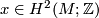 ,
, 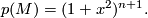
The Petrie conjecture has not been confirmed in general, but if 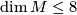 , the total Pontrjagin class of
, the total Pontrjagin class of  agrees with that of
agrees with that of 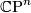 by the work of [Dejter1976] and [James1985].
According to [Hattori1978], the same is true if
by the work of [Dejter1976] and [James1985].
According to [Hattori1978], the same is true if  admits an invarint almost
complex structure with the appropriate first Chern class. Another special cases where the Petrie conjecture holds are described by [Wang1975],
[Yoshida1976], [Iberkleid1978], [Muslin1978], [Tsukada&Washiyama1979], [Masuda1981], [Dessai2002], and [Dessai&Wilking2004].
admits an invarint almost
complex structure with the appropriate first Chern class. Another special cases where the Petrie conjecture holds are described by [Wang1975],
[Yoshida1976], [Iberkleid1978], [Muslin1978], [Tsukada&Washiyama1979], [Masuda1981], [Dessai2002], and [Dessai&Wilking2004].
References
- [Dejter1976] I. J. Dejter, Smooth
 -manifolds in the homotopy type of
-manifolds in the homotopy type of 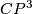 , Michigan Math. J. 23 (1976), no.1, 83–95. MR0402789 (53 #6603) Zbl 0326.57009
, Michigan Math. J. 23 (1976), no.1, 83–95. MR0402789 (53 #6603) Zbl 0326.57009
- [Dessai&Wilking2004] A. Dessai and B. Wilking, Torus actions on homotopy complex projective spaces, Math. Z. 247 (2004), no.3, 505–511. MR2114425 (2006c:57033) Zbl 1068.57034
- [Dessai2002] A. Dessai, Homotopy complex projective spaces with
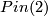 -action, Topology Appl. 122 (2002), no.3, 487–499. MR1911696 (2003f:58048) Zbl 0998.57048
-action, Topology Appl. 122 (2002), no.3, 487–499. MR1911696 (2003f:58048) Zbl 0998.57048
- [Hattori1978] A. Hattori,
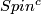 -structures and
-structures and  -actions, Invent. Math. 48 (1978), no.1, 7–31. MR508087 (80e:57051) Zbl 0395.57020
-actions, Invent. Math. 48 (1978), no.1, 7–31. MR508087 (80e:57051) Zbl 0395.57020
- [Iberkleid1978] W. Iberkleid, Pseudolinear spheres, Michigan Math. J. 25 (1978), no.3, 359–370. MR512906 (80d:57023) Zbl 0377.57008
- [James1985] D. M. James, Smooth
 actions on homotopy
actions on homotopy 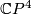 's, Michigan Math. J. 32 (1985), no.3, 259–266. MR803831 (87c:57031) Zbl 0602.57026
's, Michigan Math. J. 32 (1985), no.3, 259–266. MR803831 (87c:57031) Zbl 0602.57026
- [Masuda1981] M. Masuda, On smooth
 -actions on cohomology complex projective spaces. The case where the fixed point set consists of four connected components, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 28 (1981), no.1, 127–167. MR617869 (82i:57031) Zbl 0462.57019
-actions on cohomology complex projective spaces. The case where the fixed point set consists of four connected components, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 28 (1981), no.1, 127–167. MR617869 (82i:57031) Zbl 0462.57019
- [Muslin1978] Template:Muslin1978
- [Petrie1972] T. Petrie, Smooth
 -actions on homotopy complex projective spaces and related topics, Bull. Amer. Math. Soc. 78 (1972), 105–153. MR0296970 Zbl 0247.57010
-actions on homotopy complex projective spaces and related topics, Bull. Amer. Math. Soc. 78 (1972), 105–153. MR0296970 Zbl 0247.57010
- [Petrie1973] T. Petrie, Torus actions on homotopy complex projective spaces, Invent. Math. 20 (1973), 139–146. MR0322893 (48 #1254) Zbl 0262.57021
- [Tsukada&Washiyama1979] E. Tsukada and R. Washiyama,
 -actions on cohomology complex projective spaces with three components of the fixed point sets, Hiroshima Math. J. 9 (1979), no.1, 41–46. MR529325 (80j:57043) Zbl 0411.57037
-actions on cohomology complex projective spaces with three components of the fixed point sets, Hiroshima Math. J. 9 (1979), no.1, 41–46. MR529325 (80j:57043) Zbl 0411.57037
- [Wang1975] K. Wang, Differentiable circle group actions on homotopy complex projective spaces, Math. Ann. 214 (1975), 73–80. MR0372895 (51 #9099) Zbl 0285.57025
- [Yoshida1976] Template:Yoshida1976