Orientation covering
(→Properties) |
m |
||
| Line 17: | Line 17: | ||
As a set $\hat M$ is the set of pairs $(x, o_x)$, where $o_x$ is a local orientation of $M$ at $x$, either given by a generator of $H_n(M, M-x;\mathbb Z)$ or by an orientation of $T_xM$ in the smooth case (for the equivalence of these data see the atlas page on orientation of manifold). The map $p$ assigns $x$ to $(x,o_x)$. Since there are precisely two local orientations, the fibers of this map have cardinality $2$. | As a set $\hat M$ is the set of pairs $(x, o_x)$, where $o_x$ is a local orientation of $M$ at $x$, either given by a generator of $H_n(M, M-x;\mathbb Z)$ or by an orientation of $T_xM$ in the smooth case (for the equivalence of these data see the atlas page on orientation of manifold). The map $p$ assigns $x$ to $(x,o_x)$. Since there are precisely two local orientations, the fibers of this map have cardinality $2$. | ||
| − | Next we define a topology on this set. Let $\varphi : U \to V\subset \mathbb R^n$ be a chart of $M$ (smooth, if $M$ is smooth). We orient $\mathbb R^n$ by the standard orientation given by the standard basis $e_1$, $e_2$, ..., $e_n$, from which we define a continuous local orientation by identifying the tangent space with $\mathbb R^n$. Since for a smooth manifold a tangential orientation defines a homological orientation, this also gives a homological orientation (see atlas page on orientation of manifolds). We call the standard local orientation at $x \in \mathbb R^n$ by $sto_x$. Using the chart we transport this standard orientation to $U$ by the induced map on homology or the differential in the case of tangential orientations. The local orientations given by this orientation of $U$ is a subset of $\hat M$, which we require to be open. Doing the same starting with the non-standard orientation of $\mathbb R^n$ we obtain another subset, which we also call open. We give $\hat M$ the topology generated by these open subsets, where we vary over all | + | Next we define a topology on this set. Let $\varphi : U \to V\subset \mathbb R^n$ be a [[Wikipedia:hart_(topology)#Charts|chart]] of $M$ (smooth, if $M$ is smooth). We orient $\mathbb R^n$ by the standard orientation given by the standard basis $e_1$, $e_2$, ..., $e_n$, from which we define a continuous local orientation by identifying the tangent space with $\mathbb R^n$. Since for a smooth manifold a tangential orientation defines a homological orientation, this also gives a homological orientation (see atlas page on orientation of manifolds). We call the standard local orientation at $x \in \mathbb R^n$ by $sto_x$. Using the chart we transport this standard orientation to $U$ by the induced map on homology or the differential in the case of tangential orientations. The local orientations given by this orientation of $U$ is a subset of $\hat M$, which we require to be open. Doing the same starting with the non-standard orientation of $\mathbb R^n$ we obtain another subset, which we also call open. We give $\hat M$ the topology generated by these open subsets, where we vary over all charts of $M$ (smooth charts, if $M$ is smooth). By construction these open subsets are homeomorphic to an open subset of $\mathbb R^n$, and so we obtain an atlas of $\hat M$. In the smooth case this is a smooth atlas making $\hat M$ a smooth manifold. The map $p$ is by construction a $2$-fold covering, smooth, if $M$ is smooth. By construction $\hat M$ is oriented in a tautological way. Thus we have constructed a $2$-fold covering of $M$ by an oriented manifold $\hat M$, which is smooth, if $M$ is smooth. |
{{endproof}} | {{endproof}} | ||
</wikitex> | </wikitex> | ||
| Line 24: | Line 24: | ||
<wikitex include="TeXInclude:">; | <wikitex include="TeXInclude:">; | ||
In this section we record the key properties of the orientation cover are given in Proposition \ref{prop:properties} below. | In this section we record the key properties of the orientation cover are given in Proposition \ref{prop:properties} below. | ||
| − | The orientation covering of a manifold $M$ is very closely related to the [[orientation character]] of $M$. This is a homomorphism | + | The orientation covering of a manifold $M$ is very closely related to the [[Wikipedia:Orientation_characater|orientation character]] of $M$. This is a homomorphism |
$$ w \colon \pi_1(M) \to \Z/2 $$ | $$ w \colon \pi_1(M) \to \Z/2 $$ | ||
which may be defined as follows. Fix a base-point $x \in M$ with lifts $\tilde x_1$ and $\tilde x_{-1}$ in $\hat M$. For a loop | which may be defined as follows. Fix a base-point $x \in M$ with lifts $\tilde x_1$ and $\tilde x_{-1}$ in $\hat M$. For a loop | ||
| Line 45: | Line 45: | ||
(2.) Follows immediately from (1.) since a two-fold cover of a connected space is non-trivial if and only if the total space of the covering is disconnected. | (2.) Follows immediately from (1.) since a two-fold cover of a connected space is non-trivial if and only if the total space of the covering is disconnected. | ||
| − | (3.) Follows from (1.) since $w$ classifies the orientation cover: see the page [[orientation character]]. | + | (3.) Follows from (1.) since $w$ classifies the orientation cover: see the page [[Wikipedia:Orientation_character|orientation character]]. |
(4.) Is true by construciton as stated. | (4.) Is true by construciton as stated. | ||
| Line 53: | Line 53: | ||
<!-- By the considerations above, $M$ is orientable if and only if this covering is trivial, or $M$ is non-orientable if and only if $N$ is connected. --> | <!-- By the considerations above, $M$ is orientable if and only if this covering is trivial, or $M$ is non-orientable if and only if $N$ is connected. --> | ||
{{endproof}} | {{endproof}} | ||
| − | |||
| − | |||
| − | |||
</wikitex> | </wikitex> | ||
| − | |||
== Examples == | == Examples == | ||
<wikitex>; | <wikitex>; | ||
Revision as of 16:17, 2 January 2013
|
An earlier version of this page was published in the Definitions section of the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 18:40, 7 March 2014 and the covering&diff=cur&oldid=11510 changes since publication. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
|
The user responsible for this page is Matthias Kreck. No other user may edit this page at present. |
Contents |
1 Construction
Tex syntax erroris a canonical two-fold covering of
Tex syntax error.
Theorem 1.1 c.f. [Dold1995, VIII 2.11].
LetTex syntax errorbe a
 -dimensional topological manifold.
-dimensional topological manifold.
There is an oriented manifold 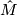 and a
and a  -fold covering
-fold covering 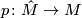 called the orientation covering.
called the orientation covering.
Tex syntax erroris a smooth, resp. piecewise linear, manifold then
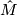 and the covering map
and the covering map  are smooth, resp. piecewise linear.
are smooth, resp. piecewise linear.
Remark 1.2.
The covering 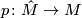 is called the orientation covering. For more information, see [Dold1995, VIII § 2].
is called the orientation covering. For more information, see [Dold1995, VIII § 2].
Proof.
As a set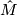 is the set of pairs
is the set of pairs 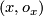 , where
, where 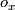 is a local orientation of
is a local orientation of Tex syntax errorat
 , either given by a generator of
, either given by a generator of 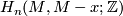 or by an orientation of
or by an orientation of 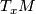 in the smooth case (for the equivalence of these data see the atlas page on orientation of manifold). The map
in the smooth case (for the equivalence of these data see the atlas page on orientation of manifold). The map  assigns
assigns  to
to 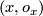 . Since there are precisely two local orientations, the fibers of this map have cardinality
. Since there are precisely two local orientations, the fibers of this map have cardinality  .
Next we define a topology on this set. Let
.
Next we define a topology on this set. Let 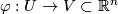 be a chart of
be a chart of Tex syntax error(smooth, if
Tex syntax erroris smooth). We orient
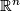 by the standard orientation given by the standard basis
by the standard orientation given by the standard basis 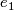 ,
, 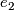 , ...,
, ..., 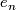 , from which we define a continuous local orientation by identifying the tangent space with
, from which we define a continuous local orientation by identifying the tangent space with 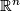 . Since for a smooth manifold a tangential orientation defines a homological orientation, this also gives a homological orientation (see atlas page on orientation of manifolds). We call the standard local orientation at
. Since for a smooth manifold a tangential orientation defines a homological orientation, this also gives a homological orientation (see atlas page on orientation of manifolds). We call the standard local orientation at 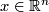 by
by 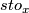 . Using the chart we transport this standard orientation to
. Using the chart we transport this standard orientation to  by the induced map on homology or the differential in the case of tangential orientations. The local orientations given by this orientation of
by the induced map on homology or the differential in the case of tangential orientations. The local orientations given by this orientation of  is a subset of
is a subset of 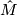 , which we require to be open. Doing the same starting with the non-standard orientation of
, which we require to be open. Doing the same starting with the non-standard orientation of 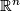 we obtain another subset, which we also call open. We give
we obtain another subset, which we also call open. We give 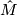 the topology generated by these open subsets, where we vary over all charts of
the topology generated by these open subsets, where we vary over all charts of Tex syntax error(smooth charts, if
Tex syntax erroris smooth). By construction these open subsets are homeomorphic to an open subset of
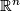 , and so we obtain an atlas of
, and so we obtain an atlas of 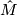 . In the smooth case this is a smooth atlas making
. In the smooth case this is a smooth atlas making 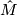 a smooth manifold. The map
a smooth manifold. The map  is by construction a
is by construction a  -fold covering, smooth, if
-fold covering, smooth, if Tex syntax erroris smooth. By construction
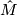 is oriented in a tautological way. Thus we have constructed a
is oriented in a tautological way. Thus we have constructed a  -fold covering of
-fold covering of Tex syntax errorby an oriented manifold
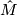 , which is smooth, if
, which is smooth, if Tex syntax erroris smooth.

2 Properties
In this section we record the key properties of the orientation cover are given in Proposition \ref{prop:properties} below.
The orientation covering of a manifoldTex syntax erroris very closely related to the orientation character of
Tex syntax error. This is a homomorphism
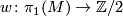
which may be defined as follows. Fix a base-point 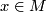 with lifts
with lifts 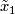 and
and 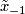 in
in 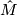 . For a loop
. For a loop
![\gamma \colon ([0, 1], \{0, 1\}) \to (M, x)](/images/math/a/e/b/aeb2bc492307160daa03d04a83a540f3.png) based at
based at  , let
, let ![\tilde \gamma \colon [0, 1] \to M](/images/math/1/5/c/15cac579d1f09184b4a1765132c3ab09.png) be the lift of
be the lift of 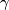 with
with 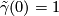 and define
and define  on the homotopy class of
on the homotopy class of 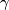 by
by
![\displaystyle w([\gamma]) := \left\{ \begin{array}{rc} 1 & \text{if $\tilde{\gamma}(1) = x_1$} \\ -1 & \text{if $\tilde{\gamma}(1) = x_{-1}$} \end{array} \right.](/images/math/4/0/a/40a42473791dfcee4b6cd72a06648499.png)
Proposition 2.1.
Let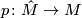 be the orientation covering of a topological manifold
be the orientation covering of a topological manifold Tex syntax error.
-
Tex syntax error
is orientable if and only if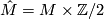 and
and  is the projection to
is the projection to Tex syntax error
. - Converely, if
Tex syntax error
is connected thenTex syntax error
is non-orientable if and only if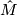 is connected.
is connected.
-
Tex syntax error
is orientable if and only if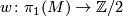 is the zero homomorphism.
is the zero homomorphism.
- By construction, the deck transformation of orientation covering is orientation reversing.
- If
 is an oriented manifold and
is an oriented manifold and 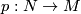 is a
is a  -fold covering with orientation reversing deck transformation, then
-fold covering with orientation reversing deck transformation, then 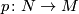 is isomorphic to the orientation covering.
is isomorphic to the orientation covering.
Proof.
(1.) IfTex syntax erroris orientable, we pick an orientation and see that
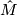 is the disjoint union of
is the disjoint union of 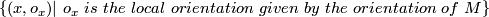 and its complement, so it is isomorphic to the trivial covering
and its complement, so it is isomorphic to the trivial covering 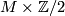 . In turn if the orientation covering is trivial it decomposes
. In turn if the orientation covering is trivial it decomposes 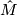 into to open (and thus oriented) subsets homeomorphic to
into to open (and thus oriented) subsets homeomorphic to Tex syntax errorand so
Tex syntax erroris orientable.
(2.) Follows immediately from (1.) since a two-fold cover of a connected space is non-trivial if and only if the total space of the covering is disconnected.
(3.) Follows from (1.) since  classifies the orientation cover: see the page orientation character.
classifies the orientation cover: see the page orientation character.
(4.) Is true by construciton as stated.
(5.) We have a map 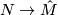 by mapping
by mapping 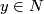 to
to 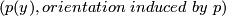 . It is easily checked that his is an isomorphism of these two coverings.
. It is easily checked that his is an isomorphism of these two coverings.

3 Examples
We give a list of basic in interesting orientation double coverings.
- If
Tex syntax error
is orientable then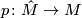 is isomorphic to the projection
is isomorphic to the projection 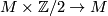 .
.
- If
 is even,
is even, 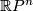 is non-orienable and with orientation cover
is non-orienable and with orientation cover 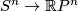 . The deck transformation
. The deck transformation
is the antipodal map on  .
.
- The orientation cover of the Klein bottle
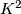 is the projection from the [[
is the projection from the [[ -torus]];
-torus]]; 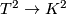 .
.
- The orientation of the open Möbius strip
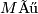 is the cylinder;
is the cylinder; 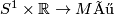 .
.
4 References
- [Dold1995] A. Dold, Lectures on algebraic topology, Springer-Verlag, 1995. MR1335915 (96c:55001) Zbl 0872.55001
5 External links
- The Encylopedia of Mathematics article on orientation.
- The Wikipedia page on the orientability.