One fixed point actions on spheres
m (→Problem) |
m |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Stub}} | {{Stub}} | ||
== Introduction == | == Introduction == | ||
| Line 25: | Line 13: | ||
* $G_0$ is a non-abelian group or the quotient group $G/G_0$ is an Oliver group. | * $G_0$ is a non-abelian group or the quotient group $G/G_0$ is an Oliver group. | ||
</wikitex> | </wikitex> | ||
| − | |||
== Results so far == | == Results so far == | ||
<wikitex>; | <wikitex>; | ||
Revision as of 14:57, 4 December 2010
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
In connection with their work on fiberings with singularities, Montgomery and Samelson [Montgomery&Samelson1946] made a comment that when a compact Lie group  acts smoothly on a sphere in such a way as to have one fixed point, it is likely that there must be a second fixed point.
Contrary to this speculation, suppose that a compact Lie group
acts smoothly on a sphere in such a way as to have one fixed point, it is likely that there must be a second fixed point.
Contrary to this speculation, suppose that a compact Lie group  acts smoothly on a sphere
acts smoothly on a sphere  with exactly one fixed point. By removing from
with exactly one fixed point. By removing from  an invariant open disk neighborhood around the single fixed point, one obtains a smooth fixed point free action of
an invariant open disk neighborhood around the single fixed point, one obtains a smooth fixed point free action of  on the disk
on the disk 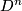 . It follows from the work of Oliver [Oliver1975] and [Oliver1976] that the identity connected component
. It follows from the work of Oliver [Oliver1975] and [Oliver1976] that the identity connected component 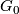 is non-abelian or the quotient group
is non-abelian or the quotient group 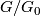 is an Oliver group. So, it is natural to ask whether in fact any such a group
is an Oliver group. So, it is natural to ask whether in fact any such a group  has a smooth one fixed point action on some sphere. The affirmative answer would confirm that the following conjecture is true.
has a smooth one fixed point action on some sphere. The affirmative answer would confirm that the following conjecture is true.
2 Problem
Conjecture 2.1. For a compact Lie group  , the following three statements are equivalent.
, the following three statements are equivalent.
- There exists a smooth action of
 on some sphere with exactly one fixed point.
on some sphere with exactly one fixed point.
- There exists a smooth action of
 on some disk without fixed points.
on some disk without fixed points.
-
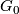 is a non-abelian group or the quotient group
is a non-abelian group or the quotient group 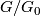 is an Oliver group.
is an Oliver group.
3 Results so far
For the following groups  , smooth one fixed point actions on spheres have been constructed.
, smooth one fixed point actions on spheres have been constructed.
-
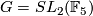 or
or 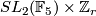 with
with 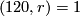 : constructed by Stein [Stein1977].
: constructed by Stein [Stein1977].
-
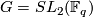 and
and 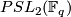 , where
, where 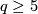 is a power of an odd prime: constructed by Petrie [Petrie1982].
is a power of an odd prime: constructed by Petrie [Petrie1982].
-
 is a finite abelian group of odd order and with three or more non-cyclic Sylow subgroups: constructed by Petrie [Petrie1982].
is a finite abelian group of odd order and with three or more non-cyclic Sylow subgroups: constructed by Petrie [Petrie1982].
-
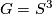 or
or  : constructed by Petrie [Petrie1982].
: constructed by Petrie [Petrie1982].
-
 is an arbitrary finite non-solvable group: constructed by Laitinen, Morimoto, and Pawałowski [Laitinen&Morimoto&Pawalowski1995].
is an arbitrary finite non-solvable group: constructed by Laitinen, Morimoto, and Pawałowski [Laitinen&Morimoto&Pawalowski1995].
-
 is an arbitrary finite Oliver group: constructed by Laitinen and Morimoto [Laitinen&Morimoto1998].
is an arbitrary finite Oliver group: constructed by Laitinen and Morimoto [Laitinen&Morimoto1998].
4 Further discussion
The results obtaine so far show that a finite group  has a smooth one fixed point action on a sphere if and only if
has a smooth one fixed point action on a sphere if and only if  is an Oliver group. However, except for the two cases solved by Petrie [Petrie1982] where
is an Oliver group. However, except for the two cases solved by Petrie [Petrie1982] where 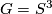 or
or  , it is not known wheter a compact Lie group
, it is not known wheter a compact Lie group  with non-abelian
with non-abelian 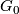 admits a smooth one fixed point action of some sphere.
admits a smooth one fixed point action of some sphere.
5 References
- [Laitinen&Morimoto&Pawalowski1995] E. Laitinen, M. Morimoto and K. Pawałowski, Deleting-inserting theorem for smooth actions of finite nonsolvable groups on spheres, Comment. Math. Helv. 70 (1995), no.1, 10–38. MR1314939 (96b:57043) Zbl 0843.57034
- [Laitinen&Morimoto1998] E. Laitinen and M. Morimoto, Finite groups with smooth one fixed point actions on spheres, Forum Math. 10 (1998), no.4, 479–520. MR1631012 (99k:57078) Zbl 0905.57023
- [Montgomery&Samelson1946] D. Montgomery and H. Samelson, Fiberings with singularities, Duke Math. J. 13 (1946), 51–56. MR0015794 (7,471a) Zbl 0060.41501
- [Oliver1975] R. Oliver, Fixed-point sets of group actions on finite acyclic complexes, Comment. Math. Helv. 50 (1975), 155–177. MR0375361 (51 #11556) Zbl 0304.57020
- [Oliver1976] R. Oliver, Smooth compact Lie group actions on disks, Math. Z. 149 (1976), no.1, 79–96. MR0423390 (54 #11369) Zbl 0334.57023
- [Petrie1982] T. Petrie, One fixed point actions on spheres. I, II, Adv. in Math. 46 (1982), no.1, 3–14, 15–70. MR676986 (84b:57027) Zbl 0502.57021
- [Stein1977] E. Stein, Surgery on products with finite fundamental group, Topology 16 (1977), no.4, 473–493. MR0474336 (57 #13982) Zbl 0383.57014