One fixed point actions on spheres
(→Introduction) |
(→Introduction) |
||
| Line 15: | Line 15: | ||
<wikitex>; | <wikitex>; | ||
In connection with their work on fiberings with singularities, Montgomery and Samelson {{cite|Montgomery&Samelson1946}} made a comment that when a compact Lie group $G$ acts smoothly on a sphere in such a way as to have one fixed point, it is likely that there must be a second fixed point. | In connection with their work on fiberings with singularities, Montgomery and Samelson {{cite|Montgomery&Samelson1946}} made a comment that when a compact Lie group $G$ acts smoothly on a sphere in such a way as to have one fixed point, it is likely that there must be a second fixed point. | ||
| − | Contrary to this speculation, suppose that a compact Lie group $G$ acts smoothly on a sphere $S^n$ with exactly one fixed point. Then, by removing from $S^n$ an invariant open disk neighborhood around the single fixed point, one obtains a smooth fixed point free action of $G$ on the disk $D^n$, and therefore, by the work of Oliver {{cite|Oliver1975}} and {{cite|Oliver1976}}, the identity connected component $G_0$ is non-abelian or the quotient group $G/G_0$ is an [[Group_actions_on_disks#Oliver_group|Oliver group]]. So, it is natural to ask whether | + | Contrary to this speculation, suppose that a compact Lie group $G$ acts smoothly on a sphere $S^n$ with exactly one fixed point. Then, by removing from $S^n$ an invariant open disk neighborhood around the single fixed point, one obtains a smooth fixed point free action of $G$ on the disk $D^n$, and therefore, by the work of Oliver {{cite|Oliver1975}} and {{cite|Oliver1976}}, the identity connected component $G_0$ is non-abelian or the quotient group $G/G_0$ is an [[Group_actions_on_disks#Oliver_group|Oliver group]]. So, it is natural to ask whether in fact any such a group $G$ has a smooth one fixed point action on some sphere. |
</wikitex> | </wikitex> | ||
Revision as of 20:50, 3 December 2010
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
In connection with their work on fiberings with singularities, Montgomery and Samelson [Montgomery&Samelson1946] made a comment that when a compact Lie group  acts smoothly on a sphere in such a way as to have one fixed point, it is likely that there must be a second fixed point.
Contrary to this speculation, suppose that a compact Lie group
acts smoothly on a sphere in such a way as to have one fixed point, it is likely that there must be a second fixed point.
Contrary to this speculation, suppose that a compact Lie group  acts smoothly on a sphere
acts smoothly on a sphere  with exactly one fixed point. Then, by removing from
with exactly one fixed point. Then, by removing from  an invariant open disk neighborhood around the single fixed point, one obtains a smooth fixed point free action of
an invariant open disk neighborhood around the single fixed point, one obtains a smooth fixed point free action of  on the disk
on the disk 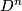 , and therefore, by the work of Oliver [Oliver1975] and [Oliver1976], the identity connected component
, and therefore, by the work of Oliver [Oliver1975] and [Oliver1976], the identity connected component 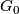 is non-abelian or the quotient group
is non-abelian or the quotient group 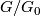 is an Oliver group. So, it is natural to ask whether in fact any such a group
is an Oliver group. So, it is natural to ask whether in fact any such a group  has a smooth one fixed point action on some sphere.
has a smooth one fixed point action on some sphere.
2 Problem
 be a compact Lie group such that the identity connected component is non-abelin or the quotient group
be a compact Lie group such that the identity connected component is non-abelin or the quotient group 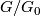 is an Oliver group. Then there exists a smooth action of
is an Oliver group. Then there exists a smooth action of  on some sphere with exactly one fixed point.
on some sphere with exactly one fixed point.
3 Results so far
- Stein [Stein1977] has obtained for the first time smooth one fixed point actions on spheres. For
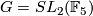 or
or 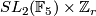 with
with 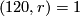 , he constructed a smooth action of
, he constructed a smooth action of  on the sphere
on the sphere 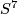 with exactly one fixed point.
with exactly one fixed point.
- Petrie [Petrie1982] described smooth one fixed point actions on spheres in the case the acting group
 is a finite abelian group of odd order and with three or more non-cyclic Sylow subgroups, as well as for
is a finite abelian group of odd order and with three or more non-cyclic Sylow subgroups, as well as for 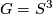 or
or 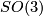 . Moreover, he announced the existence of such actions for the non-solvable groups
. Moreover, he announced the existence of such actions for the non-solvable groups 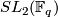 and
and 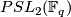 , where
, where 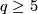 is a power of an odd prime.
is a power of an odd prime.
- Laitinen, Morimoto, and Pawałowski [Laitinen&Morimoto&Pawalowski1995] proved that any finite non-solvable group
 can act smoothly on some sphere with exactly one fixed point.
can act smoothly on some sphere with exactly one fixed point.
- Laitinen and Morimoto [Laitinen&Morimoto1998] proved that any finite Oliver group
 can acts smoothly on some sphere with exactly one fixed point.
can acts smoothly on some sphere with exactly one fixed point.
4 Further discussion
...
5 References
- [Laitinen&Morimoto&Pawalowski1995] E. Laitinen, M. Morimoto and K. Pawałowski, Deleting-inserting theorem for smooth actions of finite nonsolvable groups on spheres, Comment. Math. Helv. 70 (1995), no.1, 10–38. MR1314939 (96b:57043) Zbl 0843.57034
- [Laitinen&Morimoto1998] E. Laitinen and M. Morimoto, Finite groups with smooth one fixed point actions on spheres, Forum Math. 10 (1998), no.4, 479–520. MR1631012 (99k:57078) Zbl 0905.57023
- [Montgomery&Samelson1946] D. Montgomery and H. Samelson, Fiberings with singularities, Duke Math. J. 13 (1946), 51–56. MR0015794 (7,471a) Zbl 0060.41501
- [Oliver1975] R. Oliver, Fixed-point sets of group actions on finite acyclic complexes, Comment. Math. Helv. 50 (1975), 155–177. MR0375361 (51 #11556) Zbl 0304.57020
- [Oliver1976] R. Oliver, Smooth compact Lie group actions on disks, Math. Z. 149 (1976), no.1, 79–96. MR0423390 (54 #11369) Zbl 0334.57023
- [Petrie1982] T. Petrie, One fixed point actions on spheres. I, II, Adv. in Math. 46 (1982), no.1, 3–14, 15–70. MR676986 (84b:57027) Zbl 0502.57021
- [Stein1977] E. Stein, Surgery on products with finite fundamental group, Topology 16 (1977), no.4, 473–493. MR0474336 (57 #13982) Zbl 0383.57014