Novikov additivity I (Ex)
From Manifold Atlas
(Difference between revisions)
Tibor Macko (Talk | contribs) |
m |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | Let $(Y,X)$ be a $2n$-dimensional manifold with boundary, $n = 2k$. Consider the homomorphism $\varphi \colon H^{n} (Y,X) \rightarrow H^{n} ( | + | Let $(Y,X)$ be a $2n$-dimensional manifold with boundary, $n = 2k$. Consider the homomorphism $\varphi \colon H^{n} (Y,X) \rightarrow H^{n} (Y)$ and denote $\hat{H}^{n} (Y)$ the image of $\varphi$. Coefficients are understood to be in $\mathbb{R}$. |
The middle dimensional intersection form | The middle dimensional intersection form | ||
$$ | $$ | ||
| − | H^{n} (Y) \otimes H^{n} (Y) \rightarrow \mathbb{R} | + | H^{n} (Y, \partial Y) \otimes H^{n} (Y, \partial Y) \rightarrow \mathbb{R} |
$$ | $$ | ||
is degenerate in general. Show that the intersection form $B$ on $\hat{H}^{n} (Y)$ defined by | is degenerate in general. Show that the intersection form $B$ on $\hat{H}^{n} (Y)$ defined by | ||
| Line 19: | Line 19: | ||
Observe that the analogous statement is true if we replace manifols with boundary by Poincare pairs. | Observe that the analogous statement is true if we replace manifols with boundary by Poincare pairs. | ||
| − | Hint: section 7 of | + | Hint: section 7 of {{cite|Atiyah&Singer1968b}} |
</wikitex> | </wikitex> | ||
== References == | == References == | ||
Latest revision as of 12:28, 1 June 2012
Let 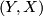 be a
be a  -dimensional manifold with boundary,
-dimensional manifold with boundary, 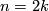 . Consider the homomorphism
. Consider the homomorphism 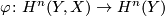 and denote
and denote 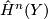 the image of
the image of 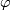 . Coefficients are understood to be in
. Coefficients are understood to be in 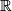 .
.
The middle dimensional intersection form
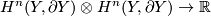
is degenerate in general. Show that the intersection form  on
on 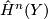 defined by
defined by
![\displaystyle B(\varphi (a), \varphi (b)) = \langle a \cup b , [Y] \rangle](/images/math/7/8/3/7837ea77f99e8d1f0cafe5f705940a2a.png)
is a non-degenerate symmetric bilinear form and let us define the signature 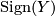 to be the signature of this form.
to be the signature of this form.
Suppose that we have also another  -dimensional manifold
-dimensional manifold 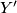 with boundary
with boundary 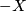 . Form the closed manifold
. Form the closed manifold 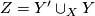 . Show that
. Show that
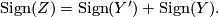
Observe that the analogous statement is true if we replace manifols with boundary by Poincare pairs.
Hint: section 7 of [Atiyah&Singer1968b]
References
- [Atiyah&Singer1968b] M. F. Atiyah and I. M. Singer, The index of elliptic operators. III, Ann. of Math. (2) 87 (1968), 546–604. MR0236952 (38 #5245) Zbl 0164.24301