Normal maps and submanifolds (Ex)
(Difference between revisions)
m |
m |
||
| Line 2: | Line 2: | ||
Let $(f, b) \colon (M, \nu_M) \to (X, \xi)$ be a [[degree one normal map]]. For simplicity, assume that $M$ and $X$ are closed oriented $\text{Cat}$-manifolds of dimension $n$. Suppose that $Y \subset X$ is a codimension $k$ oriented submanifold $X$ with normal bundle $\nu_{Y \subset X}$ and that that $f$ is [[transverse]] to $Y$. Prove the following: | Let $(f, b) \colon (M, \nu_M) \to (X, \xi)$ be a [[degree one normal map]]. For simplicity, assume that $M$ and $X$ are closed oriented $\text{Cat}$-manifolds of dimension $n$. Suppose that $Y \subset X$ is a codimension $k$ oriented submanifold $X$ with normal bundle $\nu_{Y \subset X}$ and that that $f$ is [[transverse]] to $Y$. Prove the following: | ||
# There is a canonical degree one normal map $(f|_N, b') \colon (N, \nu) \to (Y, \xi|_Y \oplus \nu_{Y \subset X})$. | # There is a canonical degree one normal map $(f|_N, b') \colon (N, \nu) \to (Y, \xi|_Y \oplus \nu_{Y \subset X})$. | ||
| − | # This defines a well-defined map $\mathcal{N}(X,\xi)\rightarrow \mathcal{N}(Y,\xi|_Y \oplus \nu_{Y \subset X})$. | + | # This defines a well-defined map $\pitchfork_Y \colon \mathcal{N}(X,\xi)\rightarrow \mathcal{N}(Y,\xi|_Y \oplus \nu_{Y \subset X})$. |
| + | Of course we have the surgery obstruction map | ||
| + | $$ \sigma \colon \mathcal{N}(Y, \xi_y \oplus \nu_{Y \subset X}) \to L_{n-k}(\pi_1(Y))$$ | ||
| + | and the composite map | ||
| + | $$ \sigma \circ \pitchfork_Y \colon \mathcal{N}(X, \xi) \to L_{n-k}(\pi_1(Y)) $$ | ||
| + | which is called the splitting obstruction map along $Y$. In addition prove the following: | ||
| + | # If $(f, b)$ is normally bordant to a homeomorphism then the splitting obstruction along $Y$ vanishes. | ||
</wikitex> | </wikitex> | ||
== References == | == References == | ||
{{#RefList:}} | {{#RefList:}} | ||
[[Category:Exercises]] | [[Category:Exercises]] | ||
Revision as of 17:16, 27 February 2012
Let 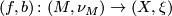 be a degree one normal map. For simplicity, assume that
be a degree one normal map. For simplicity, assume that  and
and  are closed oriented
are closed oriented 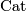 -manifolds of dimension
-manifolds of dimension  . Suppose that
. Suppose that  is a codimension
is a codimension  oriented submanifold
oriented submanifold  with normal bundle
with normal bundle 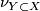 and that that
and that that  is transverse to
is transverse to  . Prove the following:
. Prove the following:
- There is a canonical degree one normal map
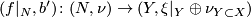 .
.
- This defines a well-defined map
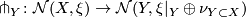 .
.
Of course we have the surgery obstruction map
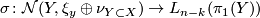
and the composite map
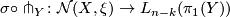
which is called the splitting obstruction map along  . In addition prove the following:
. In addition prove the following:
- If
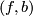 is normally bordant to a homeomorphism then the splitting obstruction along
is normally bordant to a homeomorphism then the splitting obstruction along  vanishes.
vanishes.