Normal maps and submanifolds (Ex)
(Difference between revisions)
m |
m |
||
| Line 2: | Line 2: | ||
Let $(f, b) \colon (M, \nu_M) \to (X, \xi)$ be a [[degree one normal map]]. For simplicity, assume that $M$ and $X$ are closed oriented $\text{Cat}$-manifolds of dimension $n$. Suppose that $Y \subset X$ is a codimension $k$ oriented submanifold $X$ with normal bundle $\nu_{Y \subset X}$ and that that $f$ is [[transverse]] to $Y$. Prove the following: | Let $(f, b) \colon (M, \nu_M) \to (X, \xi)$ be a [[degree one normal map]]. For simplicity, assume that $M$ and $X$ are closed oriented $\text{Cat}$-manifolds of dimension $n$. Suppose that $Y \subset X$ is a codimension $k$ oriented submanifold $X$ with normal bundle $\nu_{Y \subset X}$ and that that $f$ is [[transverse]] to $Y$. Prove the following: | ||
# There is a canonical degree one normal map $(f|_N, b') \colon (N, \nu) \to (Y, \xi|_Y \oplus \nu_{Y \subset X})$. | # There is a canonical degree one normal map $(f|_N, b') \colon (N, \nu) \to (Y, \xi|_Y \oplus \nu_{Y \subset X})$. | ||
| − | # | + | # This defines a well-defined map $\mathcal{N}(X,\xi)\rightarrow \mathcal{N}(Y,\xi|_Y \oplus \nu_{Y \subset X})$. |
</wikitex> | </wikitex> | ||
Revision as of 17:24, 26 February 2012
Let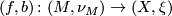 
be a degree one normal map. For simplicity, assume that 
and 
are closed oriented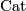 
-manifolds of dimension 
. Suppose that 
is a codimension 
oriented submanifold with normal bundle 
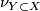and that that 
is transverse to 
. Prove the following:
- There is a canonical degree one normal map
.
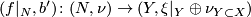- This defines a well-defined map
.
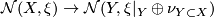