Non-reducible Spivak Normal Fibrations (Ex)
(Difference between revisions)
m |
m |
||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | + | Let $[\iota_2, \iota_3] \in \pi_4(S^2 \vee S^3)$ be the Whitehead product of the inclusion of the two factors: $[\iota_2, \iota_3]$ is the attaching map for the top cell of $S^2 \times S^3$. | |
Let $X \simeq S^2 \vee S^3 \cup_\phi E^5$ be the space obtained by attaching a $5$-cell as indicated where the map | Let $X \simeq S^2 \vee S^3 \cup_\phi E^5$ be the space obtained by attaching a $5$-cell as indicated where the map | ||
$$ \phi \colon S^4 \to S^2 \vee S^3$$ | $$ \phi \colon S^4 \to S^2 \vee S^3$$ | ||
| − | is given by $\phi = [\iota_2, \iota_3] + \iota_2 \circ \eta^2_2$ and here $\iota_i \colon S^i \to S^2 \vee S^3$ is the obvious inclusion, $[\iota_2, \iota_3]$ is the Whitehead product and $\eta^2_2 \colon S^4 \to S^2$ is essential. Show that $X$ is a Poincaré complex. | + | is given by $\phi = [\iota_2, \iota_3] + \iota_2 \circ \eta^2_2$ and here $\iota_i \colon S^i \to S^2 \vee S^3$ is the obvious inclusion, $[\iota_2, \iota_3]$ is the Whitehead product and $\eta^2_2 \colon S^4 \to S^2$ is essential. |
| + | {{beginthm|Exercise|c.f. {{citeD|Madsen&Milgram1979|2.5}}}} | ||
| + | # Show that $X$ is a Poincaré complex. | ||
| + | # Find a self-homotopy equivalence $f \colon S^2 \times S^2 \simeq S^2 \times S^2$ such that there | ||
| + | is a homotopy equivalence | ||
| + | $$ X \simeq (S^2 \times D^3) \cup_f (S^2 \times D^3).$$ | ||
| + | # Show that the Spivak normal fibration of $X$ has no vector bundle reduction. | ||
{{endthm}} | {{endthm}} | ||
| − | |||
| − | |||
| − | |||
</wikitex> | </wikitex> | ||
== References == | == References == | ||
Revision as of 23:35, 25 August 2013
Let ![[\iota_2, \iota_3] \in \pi_4(S^2 \vee S^3)](/images/math/c/2/f/c2fe9f7e9ce3f942e7e2aff69b3ab6a8.png) be the Whitehead product of the inclusion of the two factors:
be the Whitehead product of the inclusion of the two factors: ![[\iota_2, \iota_3]](/images/math/a/b/1/ab1a51d879d74a4a2c03fa1fb0804ffd.png) is the attaching map for the top cell of
is the attaching map for the top cell of 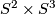 .
Let
.
Let 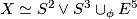 be the space obtained by attaching a
be the space obtained by attaching a 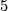 -cell as indicated where the map
-cell as indicated where the map
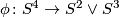
is given by ![\phi = [\iota_2, \iota_3] + \iota_2 \circ \eta^2_2](/images/math/a/0/1/a01a3398b718ede62e67fdffe2cd0f09.png) and here
and here 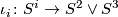 is the obvious inclusion,
is the obvious inclusion, ![[\iota_2, \iota_3]](/images/math/a/b/1/ab1a51d879d74a4a2c03fa1fb0804ffd.png) is the Whitehead product and
is the Whitehead product and 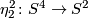 is essential.
is essential.
Exercise 0.1 c.f. [Madsen&Milgram1979, 2.5].
- Show that
 is a Poincaré complex.
is a Poincaré complex.
- Find a self-homotopy equivalence
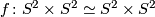 such that there
such that there
is a homotopy equivalence
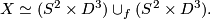
- Show that the Spivak normal fibration of
 has no vector bundle reduction.
has no vector bundle reduction.