Non-orientable quotients of the product of two 2-spheres by Z/4Z
1 Problem
Let 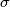 be a generator of
be a generator of 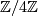 and consider the free action of
and consider the free action of 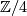 on
on 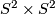 defined by
defined by

Let 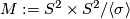 be the quotient of
be the quotient of 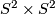 obtained from this free action.
obtained from this free action.
To understand the structure of this quotient, first, notice that 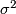 restricted to the diagonal copy of
restricted to the diagonal copy of 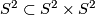 is the antipodal map.
is the antipodal map.
So the diagonal projects down to the projective plane 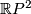 inside the quotient. Denote a normal disk bundle neighbourhood of this projective plane by
inside the quotient. Denote a normal disk bundle neighbourhood of this projective plane by  .
.
Off the diagonal, the structure of 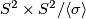 is that of a mapping cylinder. Namely, the mapping cylinder of the double cover of the lens space
is that of a mapping cylinder. Namely, the mapping cylinder of the double cover of the lens space 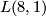 by the lens space
by the lens space 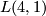 .
.
Tex syntax erroris a model for the quotient
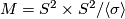 .
Modifying that mapping cylinder by taking the double covering
.
Modifying that mapping cylinder by taking the double covering 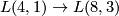 , it can be shown that
, it can be shown that Tex syntax errorand
Tex syntax errorare homotopy equivalent.
In [Hambleton&Hillmann2017] it is shown that there are exactly four topological manifolds in this homotopy type, two of which are smoothable and two which have non-trivial Kirby-Siebenmann invariant.
Question: AreTex syntax errorand
Tex syntax errordiffeomorphic?
2 References
- [Hambleton&Hillmann2017] I. Hambleton and J. Hillmann, Quotients of
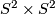 . Available at the arXiv:17172.04572.
. Available at the arXiv:17172.04572.