Microbundle
|
An earlier version of this page was published in the Definitions section of the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 12:20, 16 May 2013 and the changes since publication. |
|
The users responsible for this page are: Diarmuid Crowley, Matthias Kreck. No other users may edit this page at present. |
|
This page is being independently reviewed under the supervision of the Editorial Board. |
Contents |
1 Definition
Tex syntax errorwas first introduced in [Milnor1964] to give a model for the tangent bundle of an n-dimensional topological manifold. Later Kister [Kister1964], and independently Mazur, showed that every microbundle uniquely determines a topological
Tex syntax error-bundle; i.e. a fibre bundle with structure group the homeomorphisms of
Tex syntax errorfixing
 .
.
Definition 1.1 [Milnor1964] .
LetTex syntax errorbe a topological space. An
Tex syntax error-dimensional microbundle over
Tex syntax erroris a quadruple
Tex syntax error
where  is a space,
is a space,  and
and  are maps fitting into the following diagram
are maps fitting into the following diagram
Tex syntax error
and the following conditions hold:
Tex syntax error
.- For all
Tex syntax error
there exist open neigbourhoodTex syntax error
, an open neighbourhoodTex syntax error
ofTex syntax error
and a homeomorphismTex syntax error
which makes the following diagram commute:
![\displaystyle \xymatrix{& V \ar[dr]^{j|_V} \ar[dd]^h \\ U \ar[dr]_{\times 0} \ar[ur]^{i|_U} & & U \\ & U \times \Rr^n \ar[ur]_{p_1}}.](/images/math/9/2/8/92848a11983524dd53282be31bba8921.png)
 is called the total space of the bundle and
is called the total space of the bundle and Tex syntax errorthe base space. Two microbundles
Tex syntax error,
Tex syntax errorover the same space
Tex syntax errorare isomorphic if there exist neighbourhoods
Tex syntax errorof
Tex syntax errorand
Tex syntax errorof
Tex syntax errorand a homeomorphism
Tex syntax errormaking the following diagram commute:
![\displaystyle \xymatrix{ & V_1 \ar[dd]^{H} \ar[dr]^{j_1|_{V_1}} \\ B \ar[ur]^{i_1} \ar[dr]_{i_2} & & B \\ & V_2 \ar[ur]_{j_2|_{V_2}} }](/images/math/6/5/0/650cf2c11076ca7ab0a7ba68e744a9fa.png)
2 Examples
An important example of a microbundle is the tangent microbundle of a topological (or similarly  ) manifold
) manifold  .
Let
.
Let
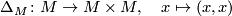
be the diagonal map for  .
.
Example 2.1 [Milnor1964, Lemma 2.1].
Let be topological (or PL)
be topological (or PL) Tex syntax error-manifold, and let
Tex syntax errorbe the projection onto the first factor. Then
Tex syntax error
Tex syntax error-dimensional microbundle, the tangent microbundle
Tex syntax errorof
 .
.
Remark 2.2.
An atlas of  gives a product atlas of
gives a product atlas of 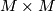 which shows that the second condition of a microbundle is fulfilled. Actually the definition of the micro tangent bundle looks a bit more like a normal bundle to the diagonal, a view which fits to the fact that the normal bundle of the diagonal of a smooth manifold
which shows that the second condition of a microbundle is fulfilled. Actually the definition of the micro tangent bundle looks a bit more like a normal bundle to the diagonal, a view which fits to the fact that the normal bundle of the diagonal of a smooth manifold  in
in 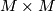 is isomorphic to its tangent bundle.
is isomorphic to its tangent bundle.
Tex syntax error-bundle.
Tex syntax errorbe a topological
Tex syntax error-bundle with zero section
Tex syntax error. Then the quadruple
Tex syntax error
Tex syntax error-dimensional microbundle.
3 The Kister-Mazur Theorem
A fundamental fact about microbundles is the following theorem, often called the Kister-Mazur theorem, proven independently by Kister and Mazur.
Theorem 3.1 [Kister1964, Theorem 2].
LetTex syntax errorbe an
Tex syntax error-dimensional microbundle over a locally finite, finite dimensional simplicial complex
Tex syntax error. Then there is a neighbourhood of
Tex syntax error,
Tex syntax errorsuch that the following hold.
-
Tex syntax error
is the total space of a topologicalTex syntax error
-bundle overTex syntax error
. -
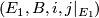 is a microbundle and the the inclusion
is a microbundle and the the inclusion Tex syntax error
is a microbundle isomorphism. - If
Tex syntax error
is any other such neighbourhood ofTex syntax error
then there is aTex syntax error
-bundle isomorphism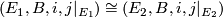 .
.
Remark 3.2.
Microbundle theory is an important part of the work by Kirby and Siebenmann [Kirby&Siebenmann1977] on smooth structures and  -structures on higher dimensional topological manifolds.
-structures on higher dimensional topological manifolds.
4 References
- [Kirby&Siebenmann1977] R. C. Kirby and L. C. Siebenmann, Foundational essays on topological manifolds, smoothings, and triangulations, Princeton University Press, Princeton, N.J., 1977. MR0645390 (58 #31082) Zbl 0361.57004
- [Kister1964] J. M. Kister, Microbundles are fibre bundles, Ann. of Math. (2) 80 (1964), 190–199. MR0180986 (31 #5216) Zbl 0131.20602
- [Milnor1964] J. Milnor, Microbundles. I, Topology 3 (1964), no.suppl. 1, 53–80. MR0161346 (28 #4553b) Zbl 0124.38404
5 External links
- The Wikipedia page about microbundles.
Tex syntax error-bundle; i.e. a fibre bundle with structure group the homeomorphisms of
Tex syntax errorfixing
 .
.
Definition 1.1 [Milnor1964] .
LetTex syntax errorbe a topological space. An
Tex syntax error-dimensional microbundle over
Tex syntax erroris a quadruple
Tex syntax error
where  is a space,
is a space,  and
and  are maps fitting into the following diagram
are maps fitting into the following diagram
Tex syntax error
and the following conditions hold:
Tex syntax error
.- For all
Tex syntax error
there exist open neigbourhoodTex syntax error
, an open neighbourhoodTex syntax error
ofTex syntax error
and a homeomorphismTex syntax error
which makes the following diagram commute:
![\displaystyle \xymatrix{& V \ar[dr]^{j|_V} \ar[dd]^h \\ U \ar[dr]_{\times 0} \ar[ur]^{i|_U} & & U \\ & U \times \Rr^n \ar[ur]_{p_1}}.](/images/math/9/2/8/92848a11983524dd53282be31bba8921.png)
 is called the total space of the bundle and
is called the total space of the bundle and Tex syntax errorthe base space. Two microbundles
Tex syntax error,
Tex syntax errorover the same space
Tex syntax errorare isomorphic if there exist neighbourhoods
Tex syntax errorof
Tex syntax errorand
Tex syntax errorof
Tex syntax errorand a homeomorphism
Tex syntax errormaking the following diagram commute:
![\displaystyle \xymatrix{ & V_1 \ar[dd]^{H} \ar[dr]^{j_1|_{V_1}} \\ B \ar[ur]^{i_1} \ar[dr]_{i_2} & & B \\ & V_2 \ar[ur]_{j_2|_{V_2}} }](/images/math/6/5/0/650cf2c11076ca7ab0a7ba68e744a9fa.png)
2 Examples
An important example of a microbundle is the tangent microbundle of a topological (or similarly  ) manifold
) manifold  .
Let
.
Let
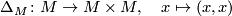
be the diagonal map for  .
.
Example 2.1 [Milnor1964, Lemma 2.1].
Let be topological (or PL)
be topological (or PL) Tex syntax error-manifold, and let
Tex syntax errorbe the projection onto the first factor. Then
Tex syntax error
Tex syntax error-dimensional microbundle, the tangent microbundle
Tex syntax errorof
 .
.
Remark 2.2.
An atlas of  gives a product atlas of
gives a product atlas of 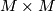 which shows that the second condition of a microbundle is fulfilled. Actually the definition of the micro tangent bundle looks a bit more like a normal bundle to the diagonal, a view which fits to the fact that the normal bundle of the diagonal of a smooth manifold
which shows that the second condition of a microbundle is fulfilled. Actually the definition of the micro tangent bundle looks a bit more like a normal bundle to the diagonal, a view which fits to the fact that the normal bundle of the diagonal of a smooth manifold  in
in 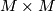 is isomorphic to its tangent bundle.
is isomorphic to its tangent bundle.
Tex syntax error-bundle.
Tex syntax errorbe a topological
Tex syntax error-bundle with zero section
Tex syntax error. Then the quadruple
Tex syntax error
Tex syntax error-dimensional microbundle.
3 The Kister-Mazur Theorem
A fundamental fact about microbundles is the following theorem, often called the Kister-Mazur theorem, proven independently by Kister and Mazur.
Theorem 3.1 [Kister1964, Theorem 2].
LetTex syntax errorbe an
Tex syntax error-dimensional microbundle over a locally finite, finite dimensional simplicial complex
Tex syntax error. Then there is a neighbourhood of
Tex syntax error,
Tex syntax errorsuch that the following hold.
-
Tex syntax error
is the total space of a topologicalTex syntax error
-bundle overTex syntax error
. -
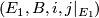 is a microbundle and the the inclusion
is a microbundle and the the inclusion Tex syntax error
is a microbundle isomorphism. - If
Tex syntax error
is any other such neighbourhood ofTex syntax error
then there is aTex syntax error
-bundle isomorphism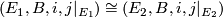 .
.
Remark 3.2.
Microbundle theory is an important part of the work by Kirby and Siebenmann [Kirby&Siebenmann1977] on smooth structures and  -structures on higher dimensional topological manifolds.
-structures on higher dimensional topological manifolds.
4 References
- [Kirby&Siebenmann1977] R. C. Kirby and L. C. Siebenmann, Foundational essays on topological manifolds, smoothings, and triangulations, Princeton University Press, Princeton, N.J., 1977. MR0645390 (58 #31082) Zbl 0361.57004
- [Kister1964] J. M. Kister, Microbundles are fibre bundles, Ann. of Math. (2) 80 (1964), 190–199. MR0180986 (31 #5216) Zbl 0131.20602
- [Milnor1964] J. Milnor, Microbundles. I, Topology 3 (1964), no.suppl. 1, 53–80. MR0161346 (28 #4553b) Zbl 0124.38404
5 External links
- The Wikipedia page about microbundles.