Microbundle
(→Introduction) |
(→Introduction) |
||
| Line 2: | Line 2: | ||
== Introduction == | == Introduction == | ||
<wikitex>; | <wikitex>; | ||
| − | The concept of | + | The concept of a <i>microbundle</i> of dimension $n$ was first introduced in {{cite|Milnor1964}} to give a model for the tangent bundle of an n-dimensional [[topological manifold]]. Later \cite{Kister1964} showed that every microbundle uniquely determines a topological $\Rr^n$-bundle. |
| Line 21: | Line 21: | ||
Let $M$ be topological $n$-manifold, and let $p_1 \colon M \times M \to M$ be the projection onto the first factor. Then | Let $M$ be topological $n$-manifold, and let $p_1 \colon M \times M \to M$ be the projection onto the first factor. Then | ||
$$ (M \times M, M, \Delta_M, p_1) $$ | $$ (M \times M, M, \Delta_M, p_1) $$ | ||
| − | is an $n$-dimensional microbundle. | + | is an $n$-dimensional microbundle, the <i>tangent microbundle</i> $\tau_M$ of $M$. |
{{endrem}} | {{endrem}} | ||
{{beginrem|Example}} Let $\pi \colon E \to B$ be a topological $\Rr^n$-bundle with zero section $s \colon B \to E$. Then $$(E, B, s, \pi)$$ | {{beginrem|Example}} Let $\pi \colon E \to B$ be a topological $\Rr^n$-bundle with zero section $s \colon B \to E$. Then $$(E, B, s, \pi)$$ | ||
Revision as of 08:09, 9 June 2012
|
An earlier version of this page was published in the Definitions section of the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 12:20, 16 May 2013 and the changes since publication. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Introduction
The concept of a microbundle of dimension  was first introduced in [Milnor1964] to give a model for the tangent bundle of an n-dimensional topological manifold. Later [Kister1964] showed that every microbundle uniquely determines a topological
was first introduced in [Milnor1964] to give a model for the tangent bundle of an n-dimensional topological manifold. Later [Kister1964] showed that every microbundle uniquely determines a topological  -bundle.
-bundle.
Definition 1.1 [Milnor1964] .
An -dimensional microbundle is a quadruple
-dimensional microbundle is a quadruple 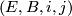 such that there is a sequence
such that there is a sequence 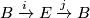
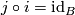
- for all
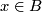 there exist open neigbourhood
there exist open neigbourhood  , an open neighbourhood
, an open neighbourhood  of
of 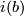 and a homeomorphism
and a homeomorphism 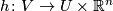
which makes the following diagram commute:
Tex syntax error
For any space  define the diagonal embedding
define the diagonal embedding
Tex syntax error
 is a differentiable
is a differentiable  -manifold the normal bundle of
-manifold the normal bundle of Tex syntax erroris the tangent bundle
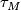 of
of  .
.
In the topological category we have:
Example 1.2 [Milnor1964, Lemma 2.1].
Let  be topological
be topological  -manifold, and let
-manifold, and let 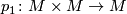 be the projection onto the first factor. Then
be the projection onto the first factor. Then
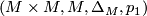
is an  -dimensional microbundle, the tangent microbundle
-dimensional microbundle, the tangent microbundle 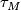 of
of  .
.
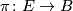 be a topological
be a topological  -bundle with zero section
-bundle with zero section 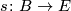 . Then
. Then 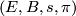
is an  -dimensional microbundle.
-dimensional microbundle.
Definition 1.4.
Two microbundles 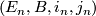 ,
, 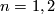 over the same space
over the same space  are isomorphic if there exist neighbourhoods
are isomorphic if there exist neighbourhoods 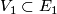 of
of 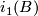 and
and 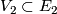 of
of 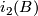 and a homeomorphism
and a homeomorphism 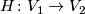 making the following diagram commute.
making the following diagram commute.
Tex syntax error
Theorem 1.5 [Kister1964, Theorem 2] .
Let 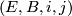 be an
be an  -dimensional microbundle. Then there is a neighbourhood of
-dimensional microbundle. Then there is a neighbourhood of 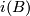 ,
, 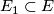 such that:
such that:
-
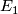 is the total space of a topological
is the total space of a topological  -bundle over
-bundle over  .
.
- The inclusion
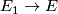 is a microbundle isomorphism
is a microbundle isomorphism
- If
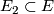 is any other such neighbourhood of
is any other such neighbourhood of 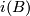 then there is a
then there is a  -bundle isomorphism
-bundle isomorphism Tex syntax error
.
2 References
- [Kister1964] J. M. Kister, Microbundles are fibre bundles, Ann. of Math. (2) 80 (1964), 190–199. MR0180986 (31 #5216) Zbl 0131.20602
- [Milnor1964] J. Milnor, Microbundles. I, Topology 3 (1964), no.suppl. 1, 53–80. MR0161346 (28 #4553b) Zbl 0124.38404