Manifold Atlas:Definition of “manifold”
(Difference between revisions)
| Line 4: | Line 4: | ||
== Definition == | == Definition == | ||
<wikitex>; | <wikitex>; | ||
| − | We assume that all manifolds are of a fixed dimension n. An '''n-dimensional manifold''' $M$ is a [[Wikipedia:Second_countable|second countable]] [[Wikipedia:Hausdorff_space|Hausdorff space]] for which every point $m \in M$ has a neighbourhood $U_m$ homeomorphic to an open subset of $\Rr^n$ or an open subset of $\Rr^n_+ = \{ x \in \Rr^n | x_1 \geq 0 \}$. The former points are the interior points of $M$. | + | We assume that all manifolds are of a fixed dimension n. An '''n-dimensional manifold''' $M$ is a [[Wikipedia:Second_countable|second countable]] [[Wikipedia:Hausdorff_space|Hausdorff space]] for which every point $m \in M$ has a neighbourhood $U_m$ homeomorphic to an open subset of $\Rr^n$ or to an open subset of $\Rr^n_+ = \{ x \in \Rr^n | x_1 \geq 0 \}$. The former points are the interior points of $M$. |
| − | * The '''interior''' of $M$, denoted $\ | + | * The '''interior''' of $M$, denoted $\mathrm{int}(M)$, is the subset of points for which $U_m \subset \Rr^n$. |
| − | * The '''boundary''' of $M$, written $\partial M$, is the compliemnt of the interior of $M$ | + | * The '''boundary''' of $M$, written $\partial M$, is the compliemnt of the interior of $M$. |
* $M$ is called '''closed''' if $M$ is compact and $\partial M$ is empty. | * $M$ is called '''closed''' if $M$ is compact and $\partial M$ is empty. | ||
Revision as of 10:29, 16 September 2009
This page defines the term “manifold” as used in the Manifold Atlas.
1 Definition
We assume that all manifolds are of a fixed dimension n. An n-dimensional manifold  is a second countable Hausdorff space for which every point
is a second countable Hausdorff space for which every point 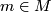 has a neighbourhood
has a neighbourhood 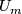 homeomorphic to an open subset of
homeomorphic to an open subset of  or to an open subset of
or to an open subset of 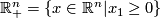 . The former points are the interior points of
. The former points are the interior points of  .
.
- The interior of
 , denoted
, denoted 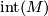 , is the subset of points for which
, is the subset of points for which 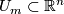 .
.
- The boundary of
 , written
, written 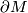 , is the compliemnt of the interior of
, is the compliemnt of the interior of  .
.
-
 is called closed if
is called closed if  is compact and
is compact and 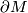 is empty.
is empty.
Extra structures
Typically, but not necessarly, the word ``manifold`` will mean  as above with extra structure. The extra structure may or may not be emphasised in notation and vocabulary.
as above with extra structure. The extra structure may or may not be emphasised in notation and vocabulary.
- A smooth manifold
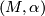 is a manifold
is a manifold  with an equivalence class of
with an equivalence class of
2 References
|
This page has not been refereed. The information given here might be incomplete or provisional. |