Links of singular points of complex hypersurfaces
Contents |
1 Introduction
The links of singular points of complex hypersurfaces provides a large class of examples of highly-connected odd dimensional manifold which are boundary highly-connected, stably parallelisable even dimensional manifolds. In the case of singular points of complex curves, the link of such a singular point is a fibered link in the  -dimensional sphere
-dimensional sphere  .
.
2 Construction and examples
Let 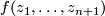 be a non-constant polynomial in
be a non-constant polynomial in 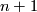 complex variables. A complex hypersurface
complex variables. A complex hypersurface  is the algebraic set consisting of points
is the algebraic set consisting of points 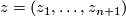 such that
such that 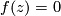 . A regular point
. A regular point 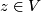 is a point at which some partial derivative
is a point at which some partial derivative 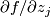 does not vanish; if at a point
does not vanish; if at a point 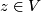 all the partial derivatives
all the partial derivatives 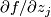 vanish,
vanish,  is called a singular point of
is called a singular point of  .
.
Near a regular point  , the complex hypersurface
, the complex hypersurface  is a smooth manifold of real dimension
is a smooth manifold of real dimension  ; in a small neighborhood of a singular point
; in a small neighborhood of a singular point  , the topology of the complex hypersurface
, the topology of the complex hypersurface  is more complicated. One way to look at the topology near
is more complicated. One way to look at the topology near  , due to Brauner, is to look at the intersection of
, due to Brauner, is to look at the intersection of  with a
with a 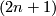 -dimensioanl sphere of small radius
-dimensioanl sphere of small radius 
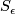 centered at
centered at  .
.
\begin{thm}
The space 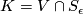 is
is  -connected.
\end{thm}
-connected.
\end{thm}
The topology of  is independent of the small paremeter
is independent of the small paremeter  , it is called the link of the singular point
, it is called the link of the singular point  .
.
\begin{thm}(Fibration Theorem)
For  sufficiently small, the space
sufficiently small, the space 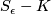 is a smooth fiber bundle over
is a smooth fiber bundle over  , with projection map
, with projection map 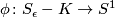 ,
, 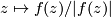 . Each fiber
. Each fiber 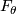 is parallelizable and has the homotopy type of a finite CW-complex of dimension
is parallelizable and has the homotopy type of a finite CW-complex of dimension  .
\end{thm}
.
\end{thm}
The fiber 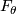 is usually called the Milnor fiber of the singular point
is usually called the Milnor fiber of the singular point  .
.
A singular point  is isolated if there is no other singular point in some small neighborhood of
is isolated if there is no other singular point in some small neighborhood of  .
.
In this special situation, the above theorems are strengthened to
\begin{thm}
Each fiber is a smooth parallelizable manifold with boundary, having the homotopy type of a bouquet of  -spheres
-spheres 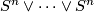 .
\end{thm}
.
\end{thm}
3 Invariants
Seen from the above section, the link  of an isolated singular point
of an isolated singular point  of a complex hypersurface
of a complex hypersurface  of complex dimension
of complex dimension  is a
is a  -connected
-connected 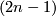 -dimensional closed smooth manifold. In high dimensional topology, these are called highly connected manifolds, since for a
-dimensional closed smooth manifold. In high dimensional topology, these are called highly connected manifolds, since for a 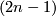 -dimensional closed manifold
-dimensional closed manifold  which is not a homotopy sphere,
which is not a homotopy sphere,  is the highest connectivity
is the highest connectivity  could have.
could have.
4 Classification/Characterization
...
5 Further discussion
...
6 References
|
This page has not been refereed. The information given here might be incomplete or provisional. |