Homotopy spheres III (Ex)
From Manifold Atlas
(Difference between revisions)
(Created page with "<wikitex>; Assume Adam's theorem that the $J$-homomorphism $J \colon \pi_{8k+\epsilon}(SO) \to \pi_{8k+\epsilon}^S$ is injective for $\epsilon = 0, 1$ and for all $k$, \cite{A...") |
m |
||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | Assume Adam's | + | Assume Adam's result that the $J$-homomorphism, $J \colon \pi_{8k+\epsilon}(SO) \to \pi_{8k+\epsilon}^S$, |
is injective for $\epsilon = 0, 1$ and for all $k$, \cite{Adams1966|Theorems 1.1 and 1.3}. | is injective for $\epsilon = 0, 1$ and for all $k$, \cite{Adams1966|Theorems 1.1 and 1.3}. | ||
{{beginthm|Exercise|\cite{Kervaire&Milnor1963|Theorem 3.1}}} | {{beginthm|Exercise|\cite{Kervaire&Milnor1963|Theorem 3.1}}} | ||
| − | + | Show that every homotopy sphere $\Sigma \in \Theta_{8k+\epsilon}$ is stably parallelisable. | |
{{endthm}} | {{endthm}} | ||
</wikitex> | </wikitex> | ||
Latest revision as of 09:49, 26 August 2013
Assume Adam's result that the 
-homomorphism, 
,
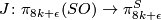is injective for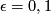 
and for all 
, [Adams1966, Theorems 1.1 and 1.3].
Exercise 0.1 [Kervaire&Milnor1963, Theorem 3.1].
Show that every homotopy sphere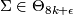 
is stably parallelisable.
References
- [Adams1966] J. F. Adams, On the groups
. IV, Topology 5 (1966), 21–71. MR0198470 (33 #6628) Zbl 0145.19902
- [Kervaire&Milnor1963] M. A. Kervaire and J. W. Milnor, Groups of homotopy spheres. I, Ann. of Math. (2) 77 (1963), 504–537. MR0148075 (26 #5584) Zbl 0115.40505
