Group actions on spheres
(→Solution for finite groups) |
|||
| Line 19: | Line 19: | ||
== Solution for finite groups == | == Solution for finite groups == | ||
| + | <wikitex>; | ||
{{beginthm|Theorem|\cite{Laitinen&Morimoto&Pawalowski1995}}} | {{beginthm|Theorem|\cite{Laitinen&Morimoto&Pawalowski1995}}} | ||
| − | For any finite non-solvable group $G$ there exists a smooth action of $G$ on some sphere with exactly one fixed point. | + | For any finite non-solvable group $G$, there exists a smooth action of $G$ on some sphere with exactly one fixed point. |
{{endthm}} | {{endthm}} | ||
| + | |||
| + | Following Laitinen and Morimoto \cite{Laitinen&Morimoto1998}, we say that a finite $G$ is an Oliver group if $G$ has a smooth fixed point free action on disk, i.e., $G$ satisfies the [[Fixed point free action on disks#Oliver groups|algebraic condition]]. | ||
{{beginthm|Theorem|\cite{Laitinen&Morimoto1998}\label{thm:one_fixed_point}}} | {{beginthm|Theorem|\cite{Laitinen&Morimoto1998}\label{thm:one_fixed_point}}} | ||
| − | For any finite Oliver group $G$ there exists a smooth action of $G$ on some sphere with exactly one fixed point. | + | For any finite Oliver group $G$, there exists a smooth action of $G$ on some sphere with exactly one fixed point. |
{{endthm}} | {{endthm}} | ||
| − | Assume that a compact Lie group $G$ acts smoothly on a sphere with exactly one fixed point $x$. Then, the Slice Theorem allows us to remove from the sphere an invariant open ball neighbourhood of $x$. As a result, we obtain a smooth fixed point free action of $G$ on a disk. Therefore | + | Assume that a compact Lie group $G$ acts smoothly on a sphere with exactly one fixed point $x$. Then, the Slice Theorem allows us to remove from the sphere an invariant open ball neighbourhood of $x$. As a result, we obtain a smooth fixed point free action of $G$ on a disk. Therefore, $G$ is an Oliver group. |
| − | + | ||
{{beginthm|Corollary|\label{cor:one_fixed_point}}} | {{beginthm|Corollary|\label{cor:one_fixed_point}}} | ||
| Line 35: | Line 37: | ||
Except for the two cases $G=S^3$ or $SO(3)$ proved by Petrie, the question whether for any compact Oliver group $G$ of positive dimension, the conclusion of Theorem \ref{thm:one_fixed_point} remains true is open. | Except for the two cases $G=S^3$ or $SO(3)$ proved by Petrie, the question whether for any compact Oliver group $G$ of positive dimension, the conclusion of Theorem \ref{thm:one_fixed_point} remains true is open. | ||
| − | + | </wikitex> | |
| − | + | ||
| − | + | ||
| − | + | ||
== References == | == References == | ||
Revision as of 15:29, 26 November 2010
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 History
In 1946, Montgomery and Samelson made a comment [Montgomery&Samelson1946] that when a compact group  acts smoothly on a sphere in such a way as to have one fixed point, it is likely that there must be a second fixed point. In 1977, Stein [Stein1977] has obtained for the first time a counterexample to this speculation. For
acts smoothly on a sphere in such a way as to have one fixed point, it is likely that there must be a second fixed point. In 1977, Stein [Stein1977] has obtained for the first time a counterexample to this speculation. For 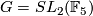 or
or 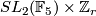 with
with 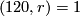 , he constructed a smooth action of
, he constructed a smooth action of  on the sphere
on the sphere 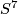 with exactly one fixed point. Then Petrie [Petrie1982] described smooth one fixed point actions on spheres in the case the acting group
with exactly one fixed point. Then Petrie [Petrie1982] described smooth one fixed point actions on spheres in the case the acting group  is a finite abelian group of odd order and with three or more non-cyclic Sylow subgroups, as well as for
is a finite abelian group of odd order and with three or more non-cyclic Sylow subgroups, as well as for 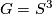 or
or  . Moreover, he announced the existence of such actions for the non-solvable groups
. Moreover, he announced the existence of such actions for the non-solvable groups 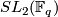 and
and 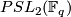 , where
, where 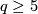 is a power of an odd prime.
is a power of an odd prime.
2 Solution for finite groups
Theorem 2.1 [Laitinen&Morimoto&Pawalowski1995].
For any finite non-solvable group  , there exists a smooth action of
, there exists a smooth action of  on some sphere with exactly one fixed point.
on some sphere with exactly one fixed point.
Following Laitinen and Morimoto [Laitinen&Morimoto1998], we say that a finite  is an Oliver group if
is an Oliver group if  has a smooth fixed point free action on disk, i.e.,
has a smooth fixed point free action on disk, i.e.,  satisfies the algebraic condition.
satisfies the algebraic condition.
Theorem 2.2 [Laitinen&Morimoto1998].
For any finite Oliver group  , there exists a smooth action of
, there exists a smooth action of  on some sphere with exactly one fixed point.
on some sphere with exactly one fixed point.
Assume that a compact Lie group  acts smoothly on a sphere with exactly one fixed point
acts smoothly on a sphere with exactly one fixed point  . Then, the Slice Theorem allows us to remove from the sphere an invariant open ball neighbourhood of
. Then, the Slice Theorem allows us to remove from the sphere an invariant open ball neighbourhood of  . As a result, we obtain a smooth fixed point free action of
. As a result, we obtain a smooth fixed point free action of  on a disk. Therefore,
on a disk. Therefore,  is an Oliver group.
is an Oliver group.
Corollary 2.3 .
A finite group  has a smooth one fixed point action on some sphere if and only if
has a smooth one fixed point action on some sphere if and only if  is an Oliver group.
is an Oliver group.
Except for the two cases 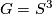 or
or  proved by Petrie, the question whether for any compact Oliver group
proved by Petrie, the question whether for any compact Oliver group  of positive dimension, the conclusion of Theorem 2.2 remains true is open.
of positive dimension, the conclusion of Theorem 2.2 remains true is open.
3 References
- [Laitinen&Morimoto&Pawalowski1995] E. Laitinen, M. Morimoto and K. Pawałowski, Deleting-inserting theorem for smooth actions of finite nonsolvable groups on spheres, Comment. Math. Helv. 70 (1995), no.1, 10–38. MR1314939 (96b:57043) Zbl 0843.57034
- [Laitinen&Morimoto1998] E. Laitinen and M. Morimoto, Finite groups with smooth one fixed point actions on spheres, Forum Math. 10 (1998), no.4, 479–520. MR1631012 (99k:57078) Zbl 0905.57023
- [Montgomery&Samelson1946] D. Montgomery and H. Samelson, Fiberings with singularities, Duke Math. J. 13 (1946), 51–56. MR0015794 (7,471a) Zbl 0060.41501
- [Petrie1982] T. Petrie, One fixed point actions on spheres. I, II, Adv. in Math. 46 (1982), no.1, 3–14, 15–70. MR676986 (84b:57027) Zbl 0502.57021
- [Stein1977] E. Stein, Surgery on products with finite fundamental group, Topology 16 (1977), no.4, 473–493. MR0474336 (57 #13982) Zbl 0383.57014