Group actions on disks
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 History
Floyd and Richardson [Floyd&Richardson1959] have constructed for the first time a smooth fixed point free action of  on a disk for
on a disk for 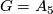 , the alternating group on five letters (see [Bredon1972, pp. 55-58] for a transparent description of the construction). Later, Greever [Greever1960]has described plenty of finite solvable groups
, the alternating group on five letters (see [Bredon1972, pp. 55-58] for a transparent description of the construction). Later, Greever [Greever1960]has described plenty of finite solvable groups  not of prime power order, which can act smoothly on disks without fixed points. Then Oliver has answered completely the question of which compact Lie groups admit smooth fixed point free actions on disks (see [Oliver1975] and [Oliver1976]).
not of prime power order, which can act smoothly on disks without fixed points. Then Oliver has answered completely the question of which compact Lie groups admit smooth fixed point free actions on disks (see [Oliver1975] and [Oliver1976]).
2 Oliver number
 be a finite group not of prime power order. Oliver in [Oliver1975] proved that the set
be a finite group not of prime power order. Oliver in [Oliver1975] proved that the set 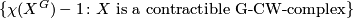
 . Therefore, the set is of the form
. Therefore, the set is of the form 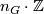 for a unique integer
for a unique integer 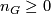 , which we refer to as the Oliver number of
, which we refer to as the Oliver number of  .
.
Oliver has determined integer 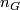 in the papers [Oliver1975], [Oliver1977], and [Oliver1978]. In particular,
in the papers [Oliver1975], [Oliver1977], and [Oliver1978]. In particular, 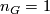 if and only if there does not exist a sequence
if and only if there does not exist a sequence 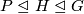 of normal subgroups such that
of normal subgroups such that  is a
is a  -group,
-group, 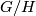 is a
is a  -group, and
-group, and 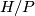 is cyclic for two (possibly equal) primes
is cyclic for two (possibly equal) primes  and
and  . Moreover, {{cite{Oliver1977|Theorem 7}}} yields the following proposition.
. Moreover, {{cite{Oliver1977|Theorem 7}}} yields the following proposition.
Proposition 1.1.
For a finite nilpotent group  not of prime power order, the following conclusions hold:
not of prime power order, the following conclusions hold:
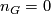 if
if  has at most one non-cyclic Sylow subgroup.
has at most one non-cyclic Sylow subgroup.
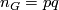 for two distinct primes
for two distinct primes  and
and  , if
, if  has just one non-cyclic
has just one non-cyclic  -Sylow and
-Sylow and  -Sylow subgroups.
-Sylow subgroups.
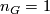 if
if  has three or more non-cyclic Sylow subgroups.
has three or more non-cyclic Sylow subgroups.
3 Oliver group
In connection with the work on smooth one fixed point actions on spheres, Laitinen and Morimoto [Laitinen&Morimoto1998] have introduced the notion of Oliver group.
Definition 2.1.
A finite group  not of prime power order is called an Oliver group if
not of prime power order is called an Oliver group if 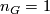 .
.
Examples of finite Oliver groups include:
- finite nilpotent (in particular, abelian) groups with three or more non-cyclic Sylow subgroups (e.g.
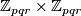 for three distinct primes
for three distinct primes  ,
,  , and
, and  ).
).
- the groups
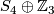 and
and 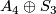 of order 72 (which are solvable but not nilpotent).
of order 72 (which are solvable but not nilpotent).
- finite non-solvable (in particular, non-trivial perfect) groups (e.g.
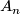 ,
, 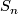 for
for 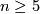 ).
).
4 Solution
Theorem 3.1 [Oliver1975].
Let  be a finite group not of prime power order. Then the following three conditions are equivalent.
be a finite group not of prime power order. Then the following three conditions are equivalent.
- There exists a smooth fixed point free action of
 on some disk.
on some disk.
- The Actions on disks without fixed points#Oliver number
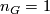 .
.
Theorem 3.2 [Oliver1976].
Let  be a compact Lie group with non-abelian identity connected component
be a compact Lie group with non-abelian identity connected component 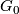 . Then there exist smooth fixed point free action of
. Then there exist smooth fixed point free action of  on some disk.
on some disk.
Corollary 3.3.
A compact Lie group  has a smooth fixed point free action on soome disk if and only if
has a smooth fixed point free action on soome disk if and only if 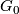 is non-abelian or
is non-abelian or 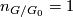 .
.
5 References
- [Bredon1972] G. E. Bredon, Introduction to compact transformation groups, Academic Press, New York, 1972. MR0413144 (54 #1265) Zbl 0484.57001
- [Floyd&Richardson1959] E. E. Floyd and R. W. Richardson, An action of a finite group on an
 -cell without stationary points. , Bull. Amer. Math. Soc. 65 (1959), 73–76. MR0100848 (20 #7276) Zbl 0088.15302
-cell without stationary points. , Bull. Amer. Math. Soc. 65 (1959), 73–76. MR0100848 (20 #7276) Zbl 0088.15302
- [Greever1960] J. Greever, Stationary points for finite transformation groups, Duke Math. J 27 (1960), 163–170. MR0110094 (22 #977) Zbl 0113.16505
- [Laitinen&Morimoto1998] E. Laitinen and M. Morimoto, Finite groups with smooth one fixed point actions on spheres, Forum Math. 10 (1998), no.4, 479–520. MR1631012 (99k:57078) Zbl 0905.57023
- [Oliver1975] R. Oliver, Fixed-point sets of group actions on finite acyclic complexes, Comment. Math. Helv. 50 (1975), 155–177. MR0375361 (51 #11556) Zbl 0304.57020
- [Oliver1976] R. Oliver, Smooth compact Lie group actions on disks, Math. Z. 149 (1976), no.1, 79–96. MR0423390 (54 #11369) Zbl 0334.57023
- [Oliver1977] R. Oliver,
 -actions on disks and permutation representations. II, Math. Z. 157 (1977), no.3, 237–263. MR0646085 (58 #31126) Zbl 0386.20002
-actions on disks and permutation representations. II, Math. Z. 157 (1977), no.3, 237–263. MR0646085 (58 #31126) Zbl 0386.20002
- [Oliver1978] R. Oliver,
 -actions on disks and permutation representations, J. Algebra 50 (1978), no.1, 44–62. MR0501044 (58 #18508) Zbl 0386.20002
-actions on disks and permutation representations, J. Algebra 50 (1978), no.1, 44–62. MR0501044 (58 #18508) Zbl 0386.20002