Group actions on disks
Marek Kaluba (Talk | contribs) (→Results) |
Marek Kaluba (Talk | contribs) (→Results) |
||
| Line 80: | Line 80: | ||
{{endthm}} | {{endthm}} | ||
| − | Let $G$ be a finite group. For two distinct primes $p$ and $q$, ''a $pq$-element'' of $G$ is an element of order $pq$. | + | Let $G$ be a finite group. For two distinct primes $p$ and $q$, ''a $pq$-element'' of $G$ is an element of order $pq$. One says that $G$ ''has $pq$-dihedral subquotient'' if $G$ contains two subgroups $H$ and $N\trianglelefteq H$ ($N$ normal in $H$) such that $H/N$ is isomorphic to the dihedral group of order $2pq$. Finally, denote by $G_2$ a $2$-Sylow subgroup of $G$. |
The class of finite groups $G$ not of prime power order divides into the following six mutually disjoint classes. | The class of finite groups $G$ not of prime power order divides into the following six mutually disjoint classes. | ||
Revision as of 15:20, 27 November 2010
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Topological actions
2 Smooth actions
2.1 Fixed point free
2.1.1 History
Floyd and Richardson [Floyd&Richardson1959] have constructed for the first time a smooth fixed point free action of  on a disk for
on a disk for 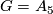 , the alternating group on five letters (see [Bredon1972, pp. 55-58] for a transparent description of the construction). Next, Greever [Greever1960] has described plenty of finite solvable groups
, the alternating group on five letters (see [Bredon1972, pp. 55-58] for a transparent description of the construction). Next, Greever [Greever1960] has described plenty of finite solvable groups  , which can act smoothly on disks without fixed points. Then, Oliver [Oliver1975] and [Oliver1976], has answered completely the question of which compact Lie groups admit smooth fixed point free actions on disks.
, which can act smoothly on disks without fixed points. Then, Oliver [Oliver1975] and [Oliver1976], has answered completely the question of which compact Lie groups admit smooth fixed point free actions on disks.
2.1.2 Oliver number
 be a finite group not of prime power order. Oliver in [Oliver1975] proved that the set
be a finite group not of prime power order. Oliver in [Oliver1975] proved that the set 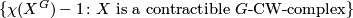
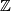 . Therefore, the set is of the form
. Therefore, the set is of the form 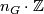 for a unique integer
for a unique integer 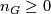 , which we refer to as the Oliver number of
, which we refer to as the Oliver number of  .
.
Oliver has determined integer 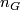 in the papers [Oliver1975], [Oliver1977], and [Oliver1978]. In particular, the following lemma holds.
in the papers [Oliver1975], [Oliver1977], and [Oliver1978]. In particular, the following lemma holds.
Lemma 2.1 (Oliver Lemma).
For a finite group  not of prime power order,
not of prime power order, 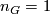 if and only if there does not exist a sequence
if and only if there does not exist a sequence 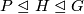 of normal subgroups such that
of normal subgroups such that  is a
is a  -group,
-group, 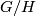 is a
is a  -group, and
-group, and 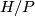 is cyclic for two (possibly the same) primes
is cyclic for two (possibly the same) primes  and
and  .
.
Moreover, the work [Oliver1977, Theorem 7] yields the following proposition.
Proposition 2.2.
For a finite nilpotent group  not of prime power order, the following conclusions hold:
not of prime power order, the following conclusions hold:
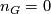 if
if  has at most one non-cyclic Sylow subgroup.
has at most one non-cyclic Sylow subgroup.
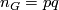 for two distinct primes
for two distinct primes  and
and  , if
, if  has just one non-cyclic
has just one non-cyclic  -Sylow and
-Sylow and  -Sylow subgroups.
-Sylow subgroups.
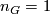 if
if  has three or more non-cyclic Sylow subgroups.
has three or more non-cyclic Sylow subgroups.
The notion of the Oliver number 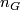 extends to compact Lie groups
extends to compact Lie groups  as follows.
as follows.
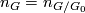 if
if 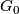 is abelian and
is abelian and 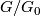 is not of prime power order.
is not of prime power order.
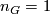 if
if 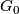 is non-abelian (see [Oliver1976]).
is non-abelian (see [Oliver1976]).
2.1.3 Oliver group
In connection with the work on smooth one fixed point actions on spheres, Laitinen and Morimoto [Laitinen&Morimoto1998] have introduced the notion of Oliver group.
Definition 2.3.
A finite group  not of prime power order is called an Oliver group if
not of prime power order is called an Oliver group if 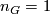 .
.
Examples of finite Oliver groups include:
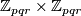 for three distinct primes
for three distinct primes  ,
,  , and
, and Tex syntax error
.- the groups
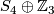 and
and 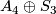 of order 72 (which are solvable but not nilpotent).
of order 72 (which are solvable but not nilpotent).
- finite non-solvable (in particular, non-trivial perfect) groups (e.g.
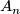 ,
, 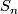 for
for 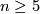 ).
).
2.1.4 Results
The results of Oliver [Oliver1975] and [Oliver1976], are summarized in the following theorem.
Theorem 2.4.
A compact Lie group  has a smooth fixed point free action on some disk if and only if at least one of the following condition holds.
has a smooth fixed point free action on some disk if and only if at least one of the following condition holds.
- The identity connected component
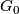 of
of  is non-abelian.
is non-abelian.
- The quotient
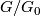 is not of prime power order and
is not of prime power order and 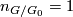 .
.
2.2 Fixed point sets
2.2.1 History
2.2.2 Results
Let  be a compact Lie group such that the identity connected component
be a compact Lie group such that the identity connected component 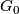 of
of  is non-abelian, or the quotient
is non-abelian, or the quotient 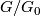 is not of prime power order. Oliver [Oliver1975], [Oliver1976] has defined an integer
is not of prime power order. Oliver [Oliver1975], [Oliver1976] has defined an integer 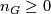 , which we refer to as the Oliver number of
, which we refer to as the Oliver number of  . Recall that
. Recall that 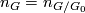 when
when 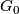 is abelian, and otherwise
is abelian, and otherwise 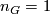 .
.
Theorem 2.5 ([Oliver1975],[Oliver1976]).
Let  be a compact Lie group such that the identity connected component
be a compact Lie group such that the identity connected component 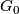 of
of  is non-abelian, or the quotient
is non-abelian, or the quotient 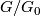 is not of prime power order. Let
is not of prime power order. Let  be a finite CW-complex. Then the following three statements are equivalent.
be a finite CW-complex. Then the following three statements are equivalent.
- The Euler-Poincaré characteristic
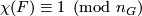 .
.
- There exist a finite contractible
 -CW-complex
-CW-complex  such that the fixed point set
such that the fixed point set 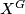 is homeomorphic to
is homeomorphic to  .
.
- There exists a smooth action of
 on a disk
on a disk 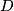 such that the fixed point set
such that the fixed point set 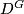 is homotopy equivalent to
is homotopy equivalent to  .
.
Let  be a finite group. For two distinct primes
be a finite group. For two distinct primes  and
and  , a
, a  -element of
-element of  is an element of order
is an element of order  . One says that
. One says that  has
has  -dihedral subquotient if
-dihedral subquotient if  contains two subgroups
contains two subgroups  and
and 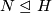 (
( normal in
normal in  ) such that
) such that 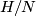 is isomorphic to the dihedral group of order
is isomorphic to the dihedral group of order 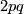 . Finally, denote by
. Finally, denote by 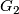 a
a  -Sylow subgroup of
-Sylow subgroup of  .
.
The class of finite groups  not of prime power order divides into the following six mutually disjoint classes.
not of prime power order divides into the following six mutually disjoint classes.
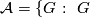 has a
has a  -dihedral subquotient
-dihedral subquotient 
 has no
has no  -dihedral subquotient,
-dihedral subquotient,  has a
has a  -element conjugate to its inverse
-element conjugate to its inverse 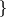
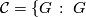 has no
has no  -element conjugate to its inverse,
-element conjugate to its inverse,  has a
has a  -element,
-element, 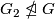
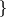
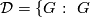 has no
has no  -element conjugate to its inverse,
-element conjugate to its inverse,  has a
has a  -element,
-element, 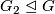
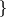
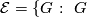 has no
has no  -element,
-element, 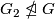
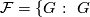 has no
has no  -element,
-element, 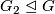
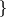
Theorem 2.6 [Oliver1996].
Let  be a finite group not of prime power order. Let
be a finite group not of prime power order. Let  be a compact smooth manifold. Then there exists a smooth action of
be a compact smooth manifold. Then there exists a smooth action of  on some disk
on some disk 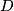 such that the fixed point
such that the fixed point 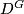 is diffeomorphic to
is diffeomorphic to  if and only if
if and only if 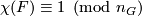 and the following conclusion about the class
and the following conclusion about the class ![[\tau_F]\in \widetilde{K}O(F)](/images/math/f/6/d/f6d05f50857ba929997be0651d9ddfef.png) holds.
holds.
- If
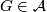 , then there is no restriction on
, then there is no restriction on ![[\tau_F]](/images/math/4/3/c/43c708b9317aab9c266b5c48be3b4214.png) .
.
- If
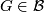 , then
, then ![c_{\mathbb{R}}([\tau_F])\in c_{\mathbb{H}}(\widetilde{K}Sp(F))+\text{qDiv}(\widetilde{K}(F))](/images/math/6/6/7/667d7e80187329075e05bc7f26cff15d.png) .
.
- If
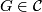 , then
, then ![[\tau_F]\in r_{\mathbb{C}}(\widetilde{K}(F))+\text{qDiv}(\widetilde{K}O(F))](/images/math/5/8/6/586cf14914ae72f61199a0e943e3dabd.png) .
.
- If
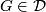 , then
, then ![[\tau_F]\in r_{\mathbb{C}}(\widetilde{K}(F))](/images/math/1/c/3/1c38081776d5ee161d8c77733a35103d.png) , i.e.,
, i.e.,  is stably complex.
is stably complex.
- If
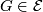 , then
, then ![[\tau_F]\in\text{qDiv}(\widetilde{K}O(F))](/images/math/1/2/7/1275ffcdcd540c823d27027ea44e8cac.png) .
.
- If
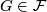 , then
, then ![[\tau_F]\in r_{\mathbb{C}}(\text{qDiv}(\widetilde{K}O(F)))](/images/math/e/0/5/e05f9a83b58704186a7d4e86529df540.png) .
.
3 References
- [Bredon1972] G. E. Bredon, Introduction to compact transformation groups, Academic Press, New York, 1972. MR0413144 (54 #1265) Zbl 0484.57001
- [Floyd&Richardson1959] E. E. Floyd and R. W. Richardson, An action of a finite group on an
 -cell without stationary points. , Bull. Amer. Math. Soc. 65 (1959), 73–76. MR0100848 (20 #7276) Zbl 0088.15302
-cell without stationary points. , Bull. Amer. Math. Soc. 65 (1959), 73–76. MR0100848 (20 #7276) Zbl 0088.15302
- [Greever1960] J. Greever, Stationary points for finite transformation groups, Duke Math. J 27 (1960), 163–170. MR0110094 (22 #977) Zbl 0113.16505
- [Laitinen&Morimoto1998] E. Laitinen and M. Morimoto, Finite groups with smooth one fixed point actions on spheres, Forum Math. 10 (1998), no.4, 479–520. MR1631012 (99k:57078) Zbl 0905.57023
- [Oliver1975] R. Oliver, Fixed-point sets of group actions on finite acyclic complexes, Comment. Math. Helv. 50 (1975), 155–177. MR0375361 (51 #11556) Zbl 0304.57020
- [Oliver1976] R. Oliver, Smooth compact Lie group actions on disks, Math. Z. 149 (1976), no.1, 79–96. MR0423390 (54 #11369) Zbl 0334.57023
- [Oliver1977] R. Oliver,
 -actions on disks and permutation representations. II, Math. Z. 157 (1977), no.3, 237–263. MR0646085 (58 #31126) Zbl 0386.20002
-actions on disks and permutation representations. II, Math. Z. 157 (1977), no.3, 237–263. MR0646085 (58 #31126) Zbl 0386.20002
- [Oliver1978] R. Oliver,
 -actions on disks and permutation representations, J. Algebra 50 (1978), no.1, 44–62. MR0501044 (58 #18508) Zbl 0386.20002
-actions on disks and permutation representations, J. Algebra 50 (1978), no.1, 44–62. MR0501044 (58 #18508) Zbl 0386.20002
- [Oliver1996] B. Oliver, Fixed point sets and tangent bundles of actions on disks and Euclidean spaces, Topology 35 (1996), no.3, 583–615. MR1396768 (97g:57059) Zbl 0861.57047