Grassmann manifolds
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Grassmann manifolds are named after Hermann Grassmann, a German school teacher in Stettin who developed basic notions of linear algebra. They play a key role in topology and geometry as the universal spaces of vector bundles. See also Grassmannian
2 Construction and examples
1 Construction
Let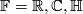 
be the real, complex or quaternion field and 
a vector space over 
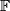of dimension 
and let 
. A Grassmannian of 
-dimensional subspaces is a set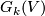 
of -dimensional subspaces. The set 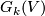is a quotient of a subset of 
consisting of linearly independent -tuples of vectors with the subspace topology. We define topology on 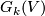as the quotient topology. Grassmannian is a homogeneous space of the general linear group. General linear group 
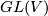acts transitively on 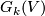with an isotropy group consisting of automorphisms preserving a given subspace. If the space is equipped with a scalar product (hermitian metric resp.) then the group of isometries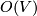 
acts transitively and the isotropy group of 
is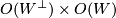 
.
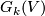is a Hausdorff, compact, connected smooth manifold of dimension 
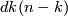. For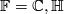 
it is also a complex manifold.Note that the Grassmann manifold 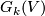around 
is locally modelled on the vector space 
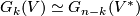. 2 The canonical bundle
The Grassmann manifold is equipped with the canonical, tautological vector bundle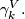 
which is a subbundle of the trivial bundle 
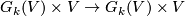. The total space is 
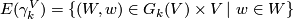The total space of the associated principal bundle is a Stiefel manifold.
The tangent bundle to Grassmaniann can be expressed in terms of the canonical bundle: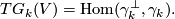 
3 Low dimensional Grassmannians
The Grassmannians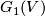 
are projective spaces, denoted 
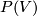. Note that 
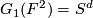, where 
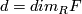. If we identify 
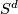with the one-point compactification of 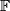the projection of the canonical principal bundle corresponds to the map 
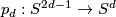given by 
where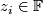 
. Note, that the same formula works for octonions 
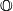, however the higher dimensional projective spaces over octonions do not exist. The maps 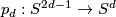for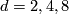 
are called the Hopf maps and they play a very important role in homotopy theory; a fibre of 
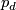is a sphere 
.
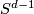4 Embeddings of Grassmannians into affine and projective space
There is an embedding of the Grassmannian 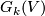in the Cartesian space 
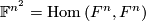which assigns to every subspace the orthogonal projection on it. If is equipped with a norm, the embedding defines a natural (operator) metric on .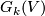
5 Infinite dimensional Grassmannians
Infinite dimensional Grassmannians. Natural inclusions of vector space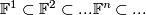 
defines inclusions of Grassmannians. The colimit of the resulting sequence is denoted 
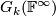and also 
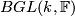. One can also take the colimit with respect to both dimension of the space and of the subspaces. We have a sequence of inclusions 
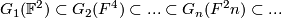and its colimit is denoted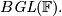 
6 Invariants
1 Homotopy groups
Homotopy groups of Grassmannians are closely related to homotopy groups of spheres via the appropriate fibration sequences. They also imply that the groups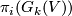 
do not depend on , if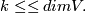 
Homotopy groups in the stable range are described by the Bott periodicity theorem.
Proposition 4.1 {(R.Bott).} For each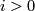 
there are isomorphisms: 
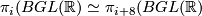and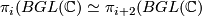 
2 Cohomology groups
...
3 Classification/Characterization
...
4 Further discussion
Grassmann manifolds are examples of coadjoint orbits [Kirillov2004].
5 References
- [Kirillov2004] A. A. Kirillov, Lectures on the orbit method, Graduate Studies in Mathematics 64, American Mathematical Society, Providence, RI, 2004. MR2069175 (2005c:22001) Zbl 02121486
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
6 External links
- The Wikipedia page on Grassmannian
