Grassmann manifolds

This page has not been refereed. The information given here might be incomplete or provisional.

1 Introduction

Grassmann manifolds are named after Hermann Grassmann, a German school teacher in Stettin who developed basic notions of linear algebra. Let

Tex syntax error

$\newcommand{\Z}{\mathbb{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\F}{\mathbb{F}} \newcommand{\bZ}{\mathbb{Z}} \newcommand{\bR}{\mathbb{R}} \newcommand{\bC}{\mathbb{C}} \newcommand{\bH}{\mathbb{H}} \newcommand{\bQ}{\mathbb{Q}} \newcommand{\bF}{\mathbb{F}} \newcommand{\bN}{\mathbb{N}} \DeclareMathOperator\id{id} % identity map \DeclareMathOperator\Sq{Sq} % Steenrod squares \DeclareMathOperator\Homeo{Homeo} % group of homeomorphisms of a topoloical space \DeclareMathOperator\Diff{Diff} % group of diffeomorphisms of a smooth manifold \DeclareMathOperator\SDiff{SDiff} % diffeomorphism under some constraint \DeclareMathOperator\Hom{Hom} % homomrphism group \DeclareMathOperator\End{End} % endomorphism group \DeclareMathOperator\Aut{Aut} % automorphism group \DeclareMathOperator\Inn{Inn} % inner automorphisms \DeclareMathOperator\Out{Out} % outer automorphism group \DeclareMathOperator\vol{vol} % volume \newcommand{\GL}{\text{GL}} % general linear group \newcommand{\SL}{\text{SL}} % special linear group \newcommand{\SO}{\text{SO}} % special orthogonal group \newcommand{\O}{\text{O}} % orthogonal group \newcommand{\SU}{\text{SU}} % special unitary group \newcommand{\Spin}{\text{Spin}} % Spin group \newcommand{\RP}{\Rr\mathrm P} % real projective space \newcommand{\CP}{\Cc\mathrm P} % complex projective space \newcommand{\HP}{\Hh\mathrm P} % quaternionic projective space \newcommand{\Top}{\mathrm{Top}} % topological category \newcommand{\PL}{\mathrm{PL}} % piecewise linear category \newcommand{\Cat}{\mathrm{Cat}} % any category \newcommand{\KS}{\text{KS}} % Kirby-Siebenmann class \newcommand{\Hud}{\text{Hud}} % Hudson torus \newcommand{\underbar}{\underline} %Classifying Spaces for Families of Subgroups \newcommand{\textup}{\text} \newcommand{\sp}{^}\newcommand{\F}{\mathbb{F}} \newcommand{\Z}{\mathbb{Z}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\HP}{\mathbb{H} P} \newcommand{\HH}{\mathbb{H}} \newcommand{\OO}{\mathbb{O}}\F$ be the real, complex or quaternion field and 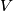$V$$V$ a vector space over 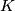$K$$K$ of dimension 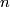$n$$n$ and let $k\leq n/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_qXpykb$$k\leq n$. 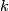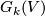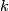A Grassmann manifolds of $k$$k$-dimensional subspaces is a set $G_k(V)/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_m0VtIg$$G_k(V)$ of $k$$k$-dimensional subspaces. 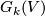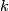The set $G_k(V)$$G_k(V)$ is a quotient of a subset of $V\times ...\times V/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_M6Afwm$$V\times ...\times V$ consisting of linearly independent $k$$k$-tuples of vectors with the subspace topology. We define topology on 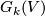$G_k(V)$$G_k(V)$ as the quotient topology.

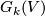Theorem 1.1 [{Milnor&Stasheff1974].} $G_k(V)$$G_k(V)$ is a Hausdorff, compact space.

Theorem 1.2 [{Milnor&Stasheff1974].} $G_k(V)$$G_k(V)$ is a connected, compact smooth manifold of dimension $dk(n-k)/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_IHRBLs$$dk(n-k)$.

Note that the Grassmann manifold 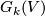$G_k(V)$$G_k(V)$ around $W\in G_k(V)/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_kNafqz$$W\in G_k(V)$ is locally modelled on the vector space $Hom (W^\bot ,W)./var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_m4SfuG$$Hom (W^\bot ,W).$ </div>

Grassmann manifold is a homogeneous space of the general linear group. General linear group 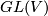$GL(V)/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_UScbXN$$GL(V)$ acts transitively on 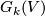$G_k(V)$$G_k(V)$ with an isotropy group consisting of automorphisms preserving a given subspace. If the space 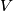$V$$V$ is equipped with a scalar product (hermitian metric resp.) then the group of isometries 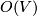$O(V)/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_G40BPV$$O(V)$ acts transitively and the isotropy group of 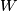$W$$W$ is $O(W^\bot)\times O(W)/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_UTKZ63$$O(W^\bot)\times O(W)$.

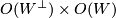The Grassmann manifold is equipped with the canonical, tautological vector bundle 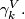$\gamma^V_k./var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_uWddPc$$\gamma^V_k.$ which is a subbundle of the trivial bundle 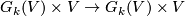$G_k(V)\times V \to G_k(V)\times V/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_u7LiEm$$G_k(V)\times V \to G_k(V)\times V$. The total space is 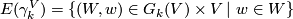$E(\gamma^V_k) = \{(W,w)\in G_k(V)\times V\, |\,\, w\in W \}/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_WVpsVw$$E(\gamma^V_k) = \{(W,w)\in G_k(V)\times V\, |\,\, w\in W \}$ The total space of the associated principal bundle is a Stiefel manifold.

Proposition 1.3 [{Milnor&Stasheff1974].} There exist a natural diffeomorphism $G_k(V)\simeq G_{n-k}(V^*)/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_C87CCH$$G_k(V)\simeq G_{n-k}(V^*)$.

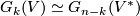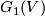The Grassmannians $G_1(V)/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_cfd1JS$$G_1(V)$ are projective spaces, denoted 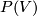$P (V)/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_m9Tri4$$P (V)$. Note that 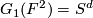$G_1(F^2)=S^d/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_yVcWgg$$G_1(F^2)=S^d$, where 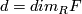$d=dim_R F/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_oGTlEs$$d=dim_R F$. If we identify 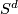$S^d/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_YXBjqF$$S^d$ with the one-point compactification of

Tex syntax error

$\F$ the projection of the canonical principal bundle corresponds to the map 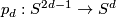$p_d :S^{2d-1}\to S^d/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_YvU515$$p_d :S^{2d-1}\to S^d$ given by $p_d(z_0,z_1)=z_0/z_1/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_oaf6Sj$$p_d(z_0,z_1)=z_0/z_1$ where

Tex syntax error

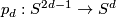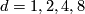$z_i\in\F$. Note, that the same formula works for octonions, however the higher dimensional projective spaces over octonions do not exist. The maps $p_d :S^{2d-1}\to S^d$$p_d :S^{2d-1}\to S^d$ for $d=1,2,4,8/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_QDwCHM$$d=1,2,4,8$ are called the Hopf maps and they play a very important role in homotopy theory; a fiber of 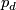$p_d/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_iUKBE1$$p_d$ is a sphere 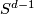$S^{d-1}/var/www/vhost/map.mpim-bonn.mpg.de/tmp/AppWikiTex/tex_Y2OKZg$$S^{d-1}$. There is an embedding of the Grassmannian

Tex syntax error

$G_k(\F^n)$ in the cartesian space

Tex syntax error

$\F^{n^2}=\Hom\,(F^n,F^n)$ which assigns to every subsapce the orthogonal projection on it. The embedding defines a natural (operator) metric on

Tex syntax error

$G_k(\F^n)$.

Prove that there is a free action of the group

Tex syntax error

$O(k,\F)$ on

Tex syntax error

$V_k(\F^n)$ sucht that the orbit space is homeomorphic to

Tex syntax error

$G_k(\F^n)$. Similarly for the noncompact Stiefel manifold.

\end{zad}

Prove that the map

Tex syntax error

$p:V_k(\F^n)\to G_k(\F^n)$ is locally trivial (even a principal

Tex syntax error

$O(k,\F)$-bundle), thus a fibration.

They are examples of coadjoint orbits [Kirillov2004]

[Milnor&Stasheff1974]

Theorem 1.4.

2 Construction and examples

...

3 Invariants

...

4 Classification/Characterization

...

5 Further discussion

...

6 References

• [Kirillov2004] A. A. Kirillov, Lectures on the orbit method, Graduate Studies in Mathematics 64, American Mathematical Society, Providence, RI, 2004. MR2069175 (2005c:22001) Zbl 02121486
• [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
• [[Template:{Milnor&Stasheff1974|[{Milnor&Stasheff1974]]] {{{Milnor&Stasheff1974}}