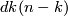Grassmann manifolds
| Line 12: | Line 12: | ||
== Introduction == | == Introduction == | ||
<wikitex>; | <wikitex>; | ||
| − | Grassmann manifolds are named after Hermann Grassmann, a German school teacher in Stettin who developed basic notions of linear algebra. Let $ | + | Grassmann manifolds are named after Hermann Grassmann, a German school teacher in Stettin who developed basic notions of linear algebra. Let $\F$ be the real, complex or quaternion field and $V$ a vector space over $K$ of dimension $n$ and let $k\leq n$. A Grassmann manifolds of $k$-dimensional subspaces is a set $G_k(V)$ of $k$-dimensional subspaces. The set $G_k(V)$ is a quotient of a subset of $V\times ...\times V$ consisting of linearly independent $k$-tuples of vectors with the subspace topology. We define topology on $G_k(V)$ as the quotient topology. |
{{beginthm|Theorem|{{cite|{Milnor&Stasheff1974}}}}} $G_k(V)$ is a Hausdorff, compact space. {{endthm}} | {{beginthm|Theorem|{{cite|{Milnor&Stasheff1974}}}}} $G_k(V)$ is a Hausdorff, compact space. {{endthm}} | ||
| Line 24: | Line 24: | ||
{{beginthm|Proposition|{{cite|{Milnor&Stasheff1974}}}}} There exist a natural diffeomorphism $G_k(V)\simeq G_{n-k}(V^*)$ {{endthm}} | {{beginthm|Proposition|{{cite|{Milnor&Stasheff1974}}}}} There exist a natural diffeomorphism $G_k(V)\simeq G_{n-k}(V^*)$ {{endthm}} | ||
| − | The Grassmannians $G_1(V)$ are projective spaces, denoted $P(V)$. Note that $G_1(F^2)=S^d$, where $d=dim_R F$. If we identify $S^d$ with the one-point compactification of $\F$ the projection $p$ corresponds to the map $p_d :S^{2d-1}\to S^d$ given by $p_d(z_0,z_1)=z_0/z_1$ where $z_i\in\F$. Note, that the same formula works for octonions, however the higher dimensional projective spaces over octonions do not exist. The maps $p_d :S^{2d-1}\to S^d$ for $d=1,2,4,8$ are called the Hopf maps and they play a very important role in homotopy theory; a fiber of $p_d$ is a sphere $S^{d-1}$. | + | The Grassmannians $G_1(V)$ are projective spaces, denoted $\P (V)$. Note that $G_1(F^2)=S^d$, where $d=dim_R F$. If we identify $S^d$ with the one-point compactification of $\F$ the projection $p$ corresponds to the map $p_d :S^{2d-1}\to S^d$ given by $p_d(z_0,z_1)=z_0/z_1$ where $z_i\in\F$. Note, that the same formula works for octonions, however the higher dimensional projective spaces over octonions do not exist. The maps $p_d :S^{2d-1}\to S^d$ for $d=1,2,4,8$ are called the Hopf maps and they play a very important role in homotopy theory; a fiber of $p_d$ is a sphere $S^{d-1}$. |
Revision as of 13:54, 26 November 2010
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Grassmann manifolds are named after Hermann Grassmann, a German school teacher in Stettin who developed basic notions of linear algebra. Let 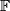 be the real, complex or quaternion field and
be the real, complex or quaternion field and  a vector space over
a vector space over  of dimension
of dimension  and let
and let  . A Grassmann manifolds of
. A Grassmann manifolds of  -dimensional subspaces is a set
-dimensional subspaces is a set 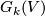 of
of  -dimensional subspaces. The set
-dimensional subspaces. The set 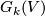 is a quotient of a subset of
is a quotient of a subset of  consisting of linearly independent
consisting of linearly independent  -tuples of vectors with the subspace topology. We define topology on
-tuples of vectors with the subspace topology. We define topology on 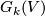 as the quotient topology.
as the quotient topology.
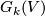 is a Hausdorff, compact space.
is a Hausdorff, compact space. Note that the Grassmann manifold 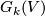 around
around  is locally modelled on the vector space
is locally modelled on the vector space  </div>
</div>
Grassmann manifold is a homogeneous space of the general linear group. General linear group 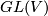 acts transitively on
acts transitively on 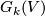 with an isotropy group consisting of automorphisms preserving a given subspace. If the space
with an isotropy group consisting of automorphisms preserving a given subspace. If the space  is equipped with a scalar product (hermitian metric resp.) then the group of isometries
is equipped with a scalar product (hermitian metric resp.) then the group of isometries 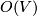 acts transitively and the isotropy group of
acts transitively and the isotropy group of  is
is 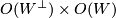 .
.
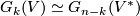
The Grassmannians 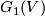 are projective spaces, denoted
are projective spaces, denoted 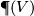 . Note that
. Note that 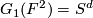 , where
, where 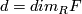 . If we identify
. If we identify 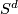 with the one-point compactification of
with the one-point compactification of 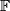 the projection
the projection  corresponds to the map
corresponds to the map 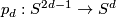 given by
given by  where
where 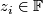 . Note, that the same formula works for octonions, however the higher dimensional projective spaces over octonions do not exist. The maps
. Note, that the same formula works for octonions, however the higher dimensional projective spaces over octonions do not exist. The maps 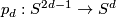 for
for 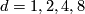 are called the Hopf maps and they play a very important role in homotopy theory; a fiber of
are called the Hopf maps and they play a very important role in homotopy theory; a fiber of 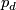 is a sphere
is a sphere 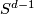 .
.
Tex syntax errorin the cartesian space
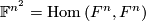 which assigns to every subsapce the orthogonal projection on it. The embedding defines a natural (operator) metric on
which assigns to every subsapce the orthogonal projection on it. The embedding defines a natural (operator) metric on Tex syntax error.
Tex syntax erroron
Tex syntax errorsucht that the orbit space is homeomorphic to
Tex syntax error. Similarly for the noncompact Stiefel manifold.
\end{zad}
Prove that the mapTex syntax erroris locally trivial (even a principal
Tex syntax error-bundle), thus a fibration.
They are examples of coadjoint orbits [Kirillov2004]
Theorem 1.4.
2 Construction and examples
...
3 Invariants
...
4 Classification/Characterization
...
5 Further discussion
...
6 References
- [Kirillov2004] A. A. Kirillov, Lectures on the orbit method, Graduate Studies in Mathematics 64, American Mathematical Society, Providence, RI, 2004. MR2069175 (2005c:22001) Zbl 02121486
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
- [[Template:{Milnor&Stasheff1974|[{Milnor&Stasheff1974]]] {{{Milnor&Stasheff1974}}