Forms and chain complexes II (Ex)
From Manifold Atlas
(Difference between revisions)
Tibor Macko (Talk | contribs) (Created page with "<wikitex>; Show that the boundary of a well-connected $1$-dimensional symmetric/quadratic complex gives a hyperbolic form. See section 2 of {{cite|Ranicki1980}} </wikitex> ==...") |
m |
||
| (3 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| + | {{beginthm|Definition|{{cite|Ranicki1980|Proposition 4.6}} }} | ||
| + | An n-dimensional $\epsilon$-symmetric/$\epsilon$-quadratic complex $(C, \phi)$/$(C, \psi)$ is called ''well-connected'' if $H_0(C)= 0$. | ||
| + | {{endthm}} | ||
| + | |||
| + | {{beginthm|Exercise}} | ||
Show that the boundary of a well-connected $1$-dimensional symmetric/quadratic complex gives a hyperbolic form. | Show that the boundary of a well-connected $1$-dimensional symmetric/quadratic complex gives a hyperbolic form. | ||
| + | {{endthm}} | ||
See section 2 of {{cite|Ranicki1980}} | See section 2 of {{cite|Ranicki1980}} | ||
Latest revision as of 16:21, 31 May 2012
Definition 0.1 [Ranicki1980, Proposition 4.6] .
An n-dimensional 
-symmetric/-quadratic complex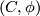 
/
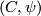is called well-connected if 
.
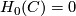Exercise 0.2.
Show that the boundary of a well-connected 
-dimensional symmetric/quadratic complex gives a hyperbolic form.
See section 2 of [Ranicki1980]
References
- [Ranicki1980] A. Ranicki, The algebraic theory of surgery. I. Foundations, Proc. London Math. Soc. (3) 40 (1980), no.1, 87–192. MR560997 (82f:57024a) Zbl 0471.57012
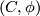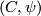-quadratic complex / is called well-connected if .
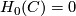Exercise 0.2.
Show that the boundary of a well-connected -dimensional symmetric/quadratic complex gives a hyperbolic form.
See section 2 of [Ranicki1980]
References
- [Ranicki1980] A. Ranicki, The algebraic theory of surgery. I. Foundations, Proc. London Math. Soc. (3) 40 (1980), no.1, 87–192. MR560997 (82f:57024a) Zbl 0471.57012
