Fake real projective spaces
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
A fake real projective space is a manifold homotopy equivalent to real projective space. Equivalently, it is the orbit space of a free involution on a (homotopy) sphere.
2 Construction and examples
Besides ordinary real projective spaces, the construction of tame free circle actions on
odd-dimensional spheres (fake complex projective spaces) gives free involutions on odd-dimensional spheres.
Free involutions on Brieskorn spheres.
[Cappell&Shaneson1976a] give examples of exotic smooth 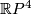 and [Fintushel&Stern1983] for fake smooth
and [Fintushel&Stern1983] for fake smooth 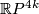 .
.
Suspension: In the topological case the join of a free involution on  with the free involution on
with the free involution on 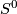 is a free involution on
is a free involution on 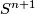 .
.
3 Invariants
Splitting invariants. Browder-Livesay invariant. Rho/Eta invariant.
4 Classification
4.1 Homotopy classification
The orbit space of a free involution on  is homotopy equivalent to
is homotopy equivalent to 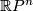 .
.
4.2 Homeomorphism classification of topological actions
Thus for a homeomorphism classification for 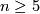 we compute the structure set of
we compute the structure set of 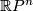 using the surgery exact sequence.
using the surgery exact sequence.
Theorem 4.1.
For 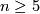 :
:
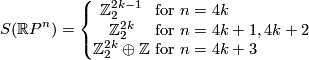
4.3 Proof
Proposition 4.2.
![[ \Rr P^n, G/Top] \cong \Zz_2^k](/images/math/4/1/0/4101cbd38312aa31d536a47d4ffd8a53.png) where
where 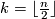 .
.
This follows from Sullivan's result about the  -local structure of
-local structure of 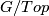 (see [Madsen&Milgram1979, Remark 4.36]),
using the Puppe sequence for
(see [Madsen&Milgram1979, Remark 4.36]),
using the Puppe sequence for 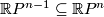 and induction.
and induction.
Proposition 4.3. The normal invariant of a homotopy projective space is the restriction of the normal invariant of its suspension.
Proposition 4.4.
The  -invariant is injective on the fibers of
-invariant is injective on the fibers of ![S(\Rr P^{4k+3})\to [\Rr P^{4k+3},G/Top]](/images/math/9/6/7/96748fae3bd6e14432053b5192d833bd.png) .
.
Proposition 4.5 [Wall1999, Theorem 13.A.1].
The  -groups of
-groups of  are:
are:
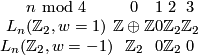
Proposition 4.6.
The surgery obstruction of 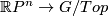 equals the obstruction for its restriction
equals the obstruction for its restriction
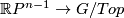 for
for  congruent to 0 and -1 modulo 4.
congruent to 0 and -1 modulo 4.
Recall that the action of the  -groups on the structure set uses the plumbing construction,
in particular the action of the image of
-groups on the structure set uses the plumbing construction,
in particular the action of the image of  is by connected sum with a homotopy sphere,
which is trivial in the topological case.
is by connected sum with a homotopy sphere,
which is trivial in the topological case.
One obtains the diagram (taken from [Lopez de Medrano1971])
![\displaystyle \xymatrix{ \Zz_2 \ar[r] & S(\Rr P^{4k+1}) \ar[d] \ar[r] & [\Rr P^{4k+1},G/Top] \ar[r] & 0 \\ 0 \ar[r] & S(\Rr P^{4k+2}) \ar[d] \ar[r] & [\Rr P^{4k+2},G/Top] \ar[u] \ar[r] & \Zz_2 \\ \Zz\oplus \Zz \ar[r] & S(\Rr P^{4k+3}) \ar[d] \ar[r] & [\Rr P^{4k+3},G/Top] \ar[u] \ar[r] & \Zz_2 \\ 0 \ar[r] & S(\Rr P^{4k+4}) \ar[d] \ar[r] & [\Rr P^{4k+4},G/Top] \ar[u] \ar[r] & \Zz_2 \\ \Zz_2 \ar[r] & S(\Rr P^{4k+5}) \ar[r] & [\Rr P^{4k+5},G/Top] \ar[u] \ar[r] & 0 }](/images/math/b/c/1/bc17e0c25b8381d76359523aed3c3714.png)
in which the preceding propositions determine all maps.
5 Further discussion
...
6 References
- [Cappell&Shaneson1976a] S. E. Cappell and J. L. Shaneson, Some new four-manifolds, Ann. of Math. (2) 104 (1976), no.1, 61–72. MR0418125 (54 #6167) Zbl 0345.57003
- [Fintushel&Stern1983] R. Fintushel and R. J. Stern, Smooth free involutions on homotopy
 -spheres, Michigan Math. J. 30 (1983), no.1, 37–51. MR694927 (84f:57025) Zbl 0543.57023
-spheres, Michigan Math. J. 30 (1983), no.1, 37–51. MR694927 (84f:57025) Zbl 0543.57023
- [Lopez de Medrano1971] S. López de Medrano, Involutions on manifolds, Springer-Verlag, 1971. MR0298698 (45 #7747) Zbl 0214.22501
- [Madsen&Milgram1979] I. Madsen and R. J. Milgram, The classifying spaces for surgery and cobordism of manifolds, Princeton University Press, Princeton, N.J., 1979. MR548575 (81b:57014) Zbl 0446.57002
- [Wall1999] C. T. C. Wall, Surgery on compact manifolds, American Mathematical Society, Providence, RI, 1999. MR1687388 (2000a:57089) Zbl 0935.57003