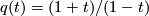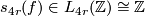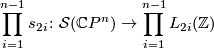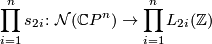Fake complex projective spaces
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
A fake complex projective space is a topological manifold which is homotopy equivalent to a complex projective space 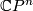 for some
for some  . The classification of these spaces was one of the early milestones in surgery theory.
. The classification of these spaces was one of the early milestones in surgery theory.
This class of manifolds is of interest for many reasons. On the one hand, they are related to certain (topological) circle actions on spheres. Moreover, they lead to easy-to-handle examples of non-tangential homotopy equivalences. In addition certain fake complex projective spaces are part of a generating set of the topological oriented cobordism groups.
2 Construction and examples
Recall that a free circle action on a manifold is called tame if the orbit space is a manifold again. Given a free tame action of the circle on a 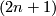 -sphere, the orbit space is a fake
-sphere, the orbit space is a fake 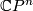 . On the other hand, if
. On the other hand, if  is a closed manifold, any homotopy equivalence
is a closed manifold, any homotopy equivalence 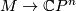 induces a principal
induces a principal  -bundle over
-bundle over  whose total space is homeomorphic to
whose total space is homeomorphic to 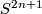 . We obtain the following result:
. We obtain the following result:
Proposition 2.1 [Wall1999, chapter 14C].
The surgery structure set of 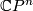 is in bijection to the set of free tame circle actions on
is in bijection to the set of free tame circle actions on 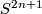 modulo equivariant homeomorphism.
modulo equivariant homeomorphism.
Edmonds [Edmonds1977] has shown that the latter set agrees with the set of all free circle actions on 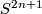 modulo a weaker relation called concordance, provided
modulo a weaker relation called concordance, provided 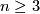 .
.
2.1 The suspension map
Given a homotopy equivalence 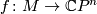 , we can suspend
, we can suspend  to obtain a fake
to obtain a fake 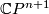 as follows: Denote by
as follows: Denote by 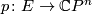 the disk bundle of the canonical complex line bundle over
the disk bundle of the canonical complex line bundle over 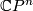 . Notice that
. Notice that 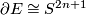 , and we obtain
, and we obtain 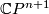 by glueing a
by glueing a 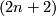 -disk to
-disk to  along the boundary. Let
along the boundary. Let 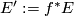 be the total space of the disk bundle pulled back bundle from
be the total space of the disk bundle pulled back bundle from  using
using  . The homotopy equivalence
. The homotopy equivalence  induces a homotopy equivalence
induces a homotopy equivalence 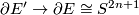 . By the Poincaré conjecture,
. By the Poincaré conjecture, 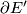 is therefore homeomorphic to
is therefore homeomorphic to 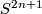 ; hence glueing the cone of
; hence glueing the cone of 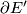 onto
onto 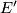 produces a
produces a 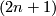 -manifold
-manifold  equipped with a homotopy equivalence to
equipped with a homotopy equivalence to 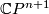 .
.
In fact, this construction defines a suspension map [Sullivan1996]
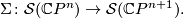
2.2 The Madsen-Milgram construction
The previous construction has been generalized as follows [Madsen&Milgram1979]: Suppose that the map  we started with is just a degree one normal map, without assuming that it is a homotopy equivalence. We can still pull back the disk bundle
we started with is just a degree one normal map, without assuming that it is a homotopy equivalence. We can still pull back the disk bundle  over
over 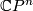 along
along  to obtain a disk bundle
to obtain a disk bundle 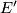 over
over  . The induced map
. The induced map 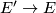 may now fail to be a homotopy equivalence, but it is a degree one normal map which restricts to a degree one normal map
may now fail to be a homotopy equivalence, but it is a degree one normal map which restricts to a degree one normal map 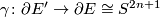 on the boundary. As
on the boundary. As 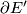 is null-bordant in
is null-bordant in  , the surgery obstruction of
, the surgery obstruction of 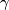 is zero. An additional argument shows that
is zero. An additional argument shows that 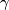 is bordant to a homotopy equivalence
is bordant to a homotopy equivalence 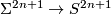 via a normal cobordism
via a normal cobordism  such that
such that
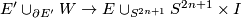
is a homotopy equivalence. Then, coning off 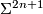 and
and 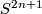 produces a homotopy equivalence
produces a homotopy equivalence 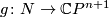 from some closed
from some closed 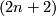 -manifold
-manifold  to
to 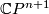 . The map
. The map  has the pleasant feature that it is transverse to
has the pleasant feature that it is transverse to 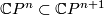 and the restriction of
and the restriction of  to a degree one normal map
to a degree one normal map 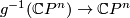 is the map
is the map  we started with.
we started with.
Hence, the suspension map  extends to a map
extends to a map
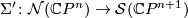
which is split injective. In fact, the following holds:
Theorem 2.2.
For 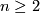 , the map
, the map 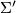 is a bijection.
is a bijection.
This follows from the classification 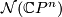 as described below: Both the domain and the target of
as described below: Both the domain and the target of 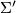 are completely described by the first
are completely described by the first  splitting invariants, and they remain unchanged under the Madsen-Milgram construction.
splitting invariants, and they remain unchanged under the Madsen-Milgram construction.
3 Invariants
3.1 Splitting invariants
Obviously the homology and homotopy groups of a fake complex projective space are isomorphic to the ones of the 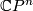 . Different fake complex projective spaces may be distinguished using the so-called splitting invariants. More precisely, for any
. Different fake complex projective spaces may be distinguished using the so-called splitting invariants. More precisely, for any 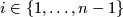 , there is a function
, there is a function
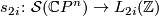
from the surgery structure set of 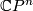 to the
to the  -groups of the integers, where
-groups of the integers, where 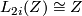 if
if  is even, and
is even, and 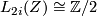 if
if  is odd.
is odd.
The splitting invariant 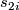 is defined as follows: Given an element
is defined as follows: Given an element 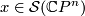 , represent it by homotopy equivalence
, represent it by homotopy equivalence 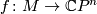 which is transverse to
which is transverse to 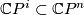 . The restriction of
. The restriction of  to a map
to a map 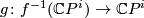 may fail to be a homotopy equivalence, but it is still a degree one normal map. Hence the surgery obstruction
may fail to be a homotopy equivalence, but it is still a degree one normal map. Hence the surgery obstruction 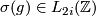 of
of  is defined. Let
is defined. Let 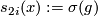 .
.
Proposition 3.1.
Under the suspension map 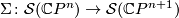 , the splitting invariants
, the splitting invariants 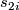 remain unchanged for
remain unchanged for 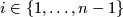 .
.
This is immediate from the construction of the suspension map. Using the classification of fake complex projective spaces described in the next section, it follows:
Corollary 3.2.
Let 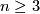 . Then the suspension map is injective, and its image is given by the homotopy equivalences
. Then the suspension map is injective, and its image is given by the homotopy equivalences 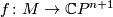 whose highest splitting invariant is zero.
whose highest splitting invariant is zero.
3.2 Rational Pontryagin classes
An interesting feature of fake complex projective spaces is that their stable tangent bundle may differ from the one of the standard 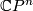 . Given a homotopy equivalence
. Given a homotopy equivalence 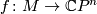 , in theory the total Hirzebruch
, in theory the total Hirzebruch 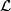 -class
-class 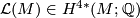 may be computed inductively from the splitting invariants using the formula [Madsen&Milgram1979, Theorem 4.9]
may be computed inductively from the splitting invariants using the formula [Madsen&Milgram1979, Theorem 4.9]
![\displaystyle s_{4i}(f) = \langle\mathcal{L}(\Cc P^{2i}) \cdot \bigl(\sum_{k\geq 1} K_{4k}(f)\vert_{\Cc P^{2i}}\bigr), [\Cc P^{2i}]\rangle,](/images/math/a/f/f/aff89978092397a800e38d4437349d39.png)
where, by [Madsen&Milgram1979, Corollary 4.22], we have
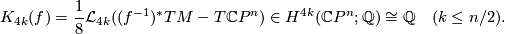
3.3 The rho-invariant
The rho-invariant of a free tame circle action on 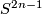 may be explicitly expressed in terms of the splitting invariants of the corresponding homotopy equivalence
may be explicitly expressed in terms of the splitting invariants of the corresponding homotopy equivalence 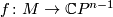 :
:
4 Classification/Characterization
The surgery classification of fake complex projective spaces was initiated by Brumfiel [Brumfiel1969a].
The surgery structure set of 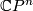 may be completely described using the splitting invariants:
may be completely described using the splitting invariants:
Thus, all possible combination of splitting invariants are realized by elements in the structure set, and two elements of the structure set agree if and only if all the splitting invariants agree.
The proof of Theorem 4.1 is surgery-theoretic. In fact the splitting invariants are defined more generally on the set of normal invariants 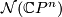 , where the surgery obstruction
, where the surgery obstruction 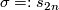 may be non-zero. Theorem 4.1 therefore follows immediately by applying the surgery exact sequence to the following homotopy-theoretic computation, which goes back to Sullivan [Sullivan1996].
may be non-zero. Theorem 4.1 therefore follows immediately by applying the surgery exact sequence to the following homotopy-theoretic computation, which goes back to Sullivan [Sullivan1996].
5 Further discussion
Fake complex projective spaces are interesting for the study of the topological oriented cobordism ring. In fact, we have
Theorem 5.1 [Madsen&Milgram1979, chapter 8]. A set of generators for the topological oriented cobordism ring modulo torsion is contained in the set consisting of the index 8 Milnor manifolds, the differentiable generators and the exotic complex projective spaces.
An interesting question is which of the fake complex projective spaces are smoothable. Sullivan [Sullivan1996] gave some examples of both smoothable and non-smoothable fake 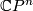 's. Weinberger [Weinberger1990] proved that for any smooth manifold
's. Weinberger [Weinberger1990] proved that for any smooth manifold  , the image of the forgetful map
, the image of the forgetful map  contains a subgroup of finite index; in particular there are infinitely many smoothable fake complex projective spaces.
contains a subgroup of finite index; in particular there are infinitely many smoothable fake complex projective spaces.
6 References
- [Brumfiel1969a] G. Brumfiel, Differentiable
 -actions on homotopy spheres, unpublished Princeton notes (1969).
-actions on homotopy spheres, unpublished Princeton notes (1969).
- [Edmonds1977] A. L. Edmonds, Taming free circle actions, Proc. Amer. Math. Soc. 62 (1977), no.2, 337–343. MR0431230 (55 #4231) Zbl 0362.57017
- [Madsen&Milgram1979] I. Madsen and R. J. Milgram, The classifying spaces for surgery and cobordism of manifolds, Princeton University Press, Princeton, N.J., 1979. MR548575 (81b:57014) Zbl 0446.57002
- [Sullivan1996] D. P. Sullivan, Triangulating and smoothing homotopy equivalences and homeomorphisms. Geometric Topology Seminar Notes, 1 (1996), 69–103. MR1434103 (98c:57027) Zbl 0871.57021
- [Wall1999] C. T. C. Wall, Surgery on compact manifolds, American Mathematical Society, Providence, RI, 1999. MR1687388 (2000a:57089) Zbl 0935.57003
- [Weinberger1990] S. Weinberger, On smooth surgery, Comm. Pure Appl. Math. 43 (1990), no.5, 695–696. MR1057237 (91c:57037) Zbl 0715.57011
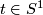
![\displaystyle \rho(t) = q(t)^n + \sum_{r=1}^{[n/2]-1} 8 \cdot s_{4r}(f) \cdot \bigl(q(t)^{n-2r} - q(t)^{n-2r-2}\bigr)\in \Cc,](/images/math/0/d/e/0de1c9c42586d80411b00186494cc170.png)