Exotic spheres
Contents |
1 Introduction
Let 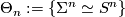 denote the set of oriented diffeomorphism classes of closed, smooth n-manifolds homotopy equivalent to
denote the set of oriented diffeomorphism classes of closed, smooth n-manifolds homotopy equivalent to  .
.
I should like to start this exotic spheres page by a link to http://www.maths.ed.ac.uk/~aar/exotic.htm to my exotic spheres home page.
This already has a large collection of original source material.
Andrew Ranicki
2 Construction and examples
Sphere bundles
The first known examples of exotic spheres were discovered by Milnor in [Milnor1956]. They are the total spaces of certain 3-sphere bundles over the 4-sphere as we now explain: the group 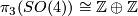 parametrises linear
parametrises linear  -sphere bundles over
-sphere bundles over  ...
...
A little later Shimada [Shimada1957] used similar techniques to show that the total spaces of certain 7-sphere bundles over the 8-sphere are exotic 15-spheres.
By Adams' solution of the Hopf-invariant 1 problem, [Adams1960], dimensions n = 1, 3, 7 and 15 are the only dimensions where an n-sphere can be fibre over an m-sphere for m<n.
2.1 Plumbing
As special case of the following construction goes back at least to [Milnor1959]
Let 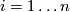 , let
, let 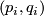 be pairs of positive integers such that
be pairs of positive integers such that 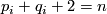 and let
and let 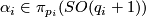 be the clutching functions of
be the clutching functions of 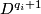 -bundles
-bundles 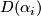 . Let
. Let  be a graph with verticies
be a graph with verticies  such that
such that 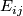 , the edge set between
, the edge set between 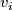 and
and 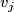 , is non-empty only if
, is non-empty only if 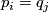 . We form the manifold
. We form the manifold 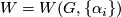 from the disjoint union of the
from the disjoint union of the 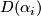 by identifying
by identifying 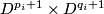 and
and 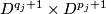 .
.
If  is simply connected the
is simply connected the 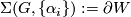 is often a homotopy sphere.
is often a homotopy sphere.
We establish some notation for bundles and graphs:
- let
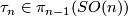 denote the tangent bundle of the
denote the tangent bundle of the  -sphere,
-sphere,
- let
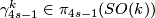 ,
, 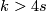 , denote a generator,
, denote a generator,
- let
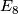 denote the
denote the 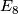 -graph,
-graph,
- let
 denote the graph with two vertices and one edge connecting them.
denote the graph with two vertices and one edge connecting them.
The we have the following exotic spheres.
-
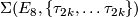 , the Milnor sphere, generates
, the Milnor sphere, generates  k>1$.
k>1$.
-
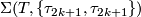 , the Kervaire sphere, generates
, the Kervaire sphere, generates 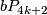
-
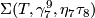 , generates
, generates 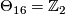 . Here
. Here 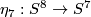 is essential.
is essential.
2.2 Twisting
By [Cerf1970] and [Smale1962a] there is an isomorphism 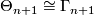 for
for  where
where 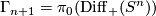 is the group of isotopy classes of orientation preserving diffeomorphisms of
is the group of isotopy classes of orientation preserving diffeomorphisms of  . The map is given by
. The map is given by
![\displaystyle \Gamma_{n+1} \to \Theta_{n+1}, ~~~~~[f] \longmapsto D^{n+1} \cup_f (-D^{n+1}).](/images/math/e/7/b/e7befcfe5bad19cfcc0035d5527a4fe8.png)
Hence one may construct exotic (n+1)-spheres by describing diffeomorphisms of  which are not isotopic to the identity.;
which are not isotopic to the identity.;
3 Invariants
Signature, Kervaire invaiant,  -invariant, Eels-Kuiper invariant,
-invariant, Eels-Kuiper invariant,  -invariant.
-invariant.
4 Classification
[Kervaire&Milnor1963], [Levine1983]
5 Further discussion
... is welcome
6 References
- [Adams1960] J. F. Adams, On the non-existence of elements of Hopf invariant one, Ann. of Math. (2) 72 (1960), 20–104. MR0141119 (25 #4530) Zbl 0096.17404
- [Cerf1970] J. Cerf, La stratification naturelle des espaces de fonctions différentiables réelles et le théorème de la pseudo-isotopie, Inst. Hautes Études Sci. Publ. Math. (1970), no.39, 5–173. MR0292089 (45 #1176) Zbl 0213.25202
- [Kervaire&Milnor1963] M. A. Kervaire and J. W. Milnor, Groups of homotopy spheres. I, Ann. of Math. (2) 77 (1963), 504–537. MR0148075 (26 #5584) Zbl 0115.40505
- [Levine1983] J. P. Levine, Lectures on groups of homotopy spheres, Algebraic and geometric topology (New Brunswick, N.J., 1983), Lecture Notes in Math., 1126 (1983), 62–95. MR802786 (87i:57031) Zbl 0576.57028
- [Milnor1956] J. Milnor, On manifolds homeomorphic to the
 -sphere, Ann. of Math. (2) 64 (1956), 399–405. MR0082103 (18,498d) Zbl 0072.18402
-sphere, Ann. of Math. (2) 64 (1956), 399–405. MR0082103 (18,498d) Zbl 0072.18402
- [Milnor1959] J. Milnor, Differentiable structures on spheres, Amer. J. Math. 81 (1959), 962–972. MR0110107 (22 #990) Zbl 0111.35501
- [Shimada1957] N. Shimada, Differentiable structures on the 15-sphere and Pontrjagin classes of certain manifolds, Nagoya Math. J. 12 (1957), 59–69. MR0096223 (20 #2715) Zbl 0145.20303
- [Smale1962a] S. Smale, On the structure of manifolds, Amer. J. Math. 84 (1962), 387–399. MR0153022 (27 #2991) Zbl 0109.41103
|
This page has not been refereed. The information given here might be incomplete or provisional. |