Exotic spheres
(→Sphere bundles) |
(→Sphere bundles) |
||
| Line 28: | Line 28: | ||
=== Sphere bundles === | === Sphere bundles === | ||
<wikitex>; | <wikitex>; | ||
| − | The first known examples of exotic spheres were discovered by Milnor in {{cite|Milnor1956}}. They are the total spaces of certain 3-[[Wikipedia:Sphere_bundle#Sphere_bundles|sphere bundles]] over the 4-sphere as we now explain: the group $\pi_3(SO(4)) \cong \Zz \oplus \Zz$ parametrises linear $3$-sphere bundles over $S^4$ where a pair $(m, n)$ gives rise to a bundle with Euler number $n$ and first Pontrjagin class $2(n+2m)$: here we orient $S^4$ and so identify $H^4(S^4; \Zz) = \Zz$. If we set $n = 1$ then the long exact homotopy sequence of a fibration and Poincare duality ensure that the manifold $\ | + | *The first known examples of exotic spheres were discovered by Milnor in {{cite|Milnor1956}}. They are the total spaces of certain 3-[[Wikipedia:Sphere_bundle#Sphere_bundles|sphere bundles]] over the 4-sphere as we now explain: the group $\pi_3(SO(4)) \cong \Zz \oplus \Zz$ parametrises linear $3$-sphere bundles over $S^4$ where a pair $(m, n)$ gives rise to a bundle with Euler number $n$ and first Pontrjagin class $2(n+2m)$: here we orient $S^4$ and so identify $H^4(S^4; \Zz) = \Zz$. If we set $n = 1$ then the long exact homotopy sequence of a fibration and Poincare duality ensure that the manifold $\Sigma^7_{m, 1}$, the total space of the bundle $(m, 1)$, is a homotopy sphere. Milnor first used a $\Zz_7$-invariant, called the $\lambda$-invariant, to show, e.g. that $\Sigma^7_{1, 1}$ is not diffeomorphic to $S^7$. A little later Kervaire and Milnor {{cite|Kervaire&Milnor1963}} show that $\Theta_7 \cong \Zz_{28}$ and Eells and Kuiper {{cite|Eells&Kuiper1962}} showed that |
| − | $$ \ | + | $$ \Sigma^7_{m, 1} = \frac{m(m-1)}{56} \in \Zz/28 \cong \Theta_7.$$ |
| − | Shimada {{cite|Shimada1957}} used similar techniques to show that the total spaces of certain 7-sphere bundles over the 8-sphere are exotic 15-spheres. | + | *Shimada {{cite|Shimada1957}} used similar techniques to show that the total spaces of certain 7-sphere bundles over the 8-sphere are exotic 15-spheres. In this case $\pi_7(SO(8)) \cong \Zz \oplus \Zz$ and the bundle $(m, n)$ has Euler number $n$ and second Pontrjagin class $6(n+2m)$. Moreover $\Theta_{15} \cong \Zz_{8,128} \oplus \Zz_2$ where the $\Zz_{8,128}$-summand is $bP_{16}$ as explained below and results of {{cite|Wall1962}} and {{cite|Eells&Kuiper1962}} combine to show that |
| + | $$ \Sigma^{15}_{m, 1} = \frac{m(m-1)}{8,128} \in \Zz_{8,128} \cong bP_{16} \subset \Theta_{15}.$$ | ||
| − | By Adams' solution of the [[Wikipedia:Hopf_invariant| Hopf-invariant]] 1 problem, {{cite|Adams1958}} and {{cite|Adams1960}}, the dimensions n = 3, 7 and 15 are the only dimensions | + | |
| + | *By Adams' solution of the [[Wikipedia:Hopf_invariant| Hopf-invariant]] 1 problem, {{cite|Adams1958}} and {{cite|Adams1960}}, the dimensions n = 3, 7 and 15 are the only dimensions in which a topological n-sphere can be fibre over an m-sphere for 0 < m < n. | ||
</wikitex> | </wikitex> | ||
Revision as of 16:51, 5 January 2010
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
A homotopy sphere 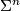 is a closed, smooth n-manifold homotopy equivalent to
is a closed, smooth n-manifold homotopy equivalent to  . The manifold
. The manifold 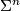 is called an exotic sphere if it is not diffeomorphic to
is called an exotic sphere if it is not diffeomorphic to  . By the Generalised Poincaré Conjecture proven by Smale, every homotopy sphere in dimension
. By the Generalised Poincaré Conjecture proven by Smale, every homotopy sphere in dimension  is homeomorphic to
is homeomorphic to  : this statement holds in dimension 2 by the classification of surfaces and was famously proven in dimension 4 in [Freedman1982] and in dimension 3 by Perelman. We define
: this statement holds in dimension 2 by the classification of surfaces and was famously proven in dimension 4 in [Freedman1982] and in dimension 3 by Perelman. We define
![\displaystyle \Theta_{n} := \{[\Sigma^n] | \Sigma^n \simeq S^n \}](/images/math/0/8/b/08bc0e5cc03477080c3f7936eafb4724.png)
to be the set of oriented diffeomorphism classes of homotopy spheres. Connected sum makes  into an abelian group with inverse given by reversing orientation.
into an abelian group with inverse given by reversing orientation.
2 Construction and examples
Exotic spheres may be constructed in a variety of ways.
2.1 Brieskorn varieties
2.2 Sphere bundles
- The first known examples of exotic spheres were discovered by Milnor in [Milnor1956]. They are the total spaces of certain 3-sphere bundles over the 4-sphere as we now explain: the group
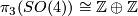 parametrises linear
parametrises linear  -sphere bundles over
-sphere bundles over  where a pair
where a pair 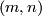 gives rise to a bundle with Euler number
gives rise to a bundle with Euler number  and first Pontrjagin class
and first Pontrjagin class 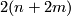 : here we orient
: here we orient  and so identify
and so identify 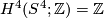 . If we set
. If we set 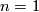 then the long exact homotopy sequence of a fibration and Poincare duality ensure that the manifold
then the long exact homotopy sequence of a fibration and Poincare duality ensure that the manifold 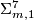 , the total space of the bundle
, the total space of the bundle 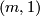 , is a homotopy sphere. Milnor first used a
, is a homotopy sphere. Milnor first used a 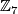 -invariant, called the
-invariant, called the  -invariant, to show, e.g. that
-invariant, to show, e.g. that 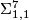 is not diffeomorphic to
is not diffeomorphic to 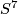 . A little later Kervaire and Milnor [Kervaire&Milnor1963] show that
. A little later Kervaire and Milnor [Kervaire&Milnor1963] show that 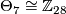 and Eells and Kuiper [Eells&Kuiper1962] showed that
and Eells and Kuiper [Eells&Kuiper1962] showed that
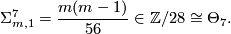
- Shimada [Shimada1957] used similar techniques to show that the total spaces of certain 7-sphere bundles over the 8-sphere are exotic 15-spheres. In this case
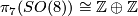 and the bundle
and the bundle  has Euler number
has Euler number  and second Pontrjagin class
and second Pontrjagin class 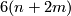 . Moreover
. Moreover 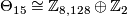 where the
where the 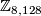 -summand is
-summand is 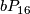 as explained below and results of [Wall1962] and [Eells&Kuiper1962] combine to show that
as explained below and results of [Wall1962] and [Eells&Kuiper1962] combine to show that
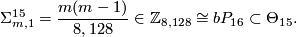
- By Adams' solution of the Hopf-invariant 1 problem, [Adams1958] and [Adams1960], the dimensions n = 3, 7 and 15 are the only dimensions in which a topological n-sphere can be fibre over an m-sphere for 0 < m < n.
2.3 Plumbing
As special case of the following construction goes back at least to [Milnor1959].
Let 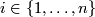 , let
, let 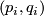 be pairs of positive integers such that
be pairs of positive integers such that 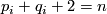 and let
and let 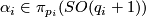 be the clutching functions of
be the clutching functions of 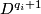 -bundles over
-bundles over 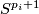
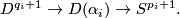
Let  be a graph with vertices
be a graph with vertices  such that the edge set between
such that the edge set between 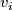 and
and 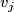 , is non-empty only if
, is non-empty only if 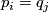 . We form the manifold
. We form the manifold 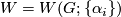 from the disjoint union of the
from the disjoint union of the 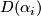 by identifying
by identifying 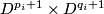 and
and 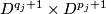 for each edge in
for each edge in  . If
. If  is simply connected then
is simply connected then
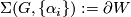
is often a homotopy sphere. We establish some notation for graphs, bundles and define
- let
 denote the graph with two vertices and one edge connecting them and define
denote the graph with two vertices and one edge connecting them and define 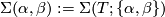 ,
,
- let
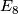 denote the
denote the 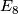 -graph,
-graph,
- let
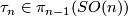 denote the tangent bundle of the
denote the tangent bundle of the  -sphere,
-sphere,
- let
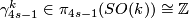 ,
, 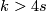 , denote a generator,
, denote a generator,
- let
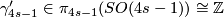 , denote a generator:
, denote a generator:
- let
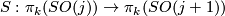 be the suspension homomorphism,
be the suspension homomorphism,
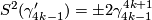 for
for 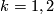 and
and 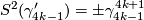 for
for 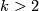 ,
,
- let
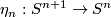 be essential.
be essential.
Then we have the following exotic spheres.
-
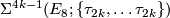 , the Milnor sphere, generates
, the Milnor sphere, generates  ,
, 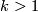 .
.
-
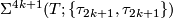 , the Kervaire sphere, generates
, the Kervaire sphere, generates 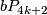 .
.
-
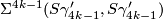 is the inverse of the Milnor sphere for
is the inverse of the Milnor sphere for 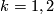 .
.
- For general
 ,
, 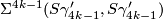 is exotic.
is exotic.
- For general
-
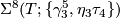 , generates
, generates 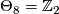 .
.
-
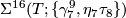 , generates
, generates 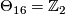 .
.
2.4 Twisting
By [Cerf1970] and [Smale1962a] there is an isomorphism 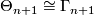 for
for  where
where 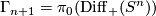 is the group of isotopy classes of orientation preserving diffeomorphisms of
is the group of isotopy classes of orientation preserving diffeomorphisms of  . The map is given by
. The map is given by
![\displaystyle \Gamma_{n+1} \to \Theta_{n+1}, ~~~~~[f] \longmapsto \Sigma_{f} := D^{n+1} \cup_f (-D^{n+1}).](/images/math/d/0/7/d072f1885886fceaf69122f3fbd9b643.png)
Hence one may construct exotic (n+1)-spheres by describing diffeomorphisms of  which are not isotopic to the identity. We give such a construction which probably goes back to Milnor: so far the earliest reference found is the problem list of the 1963 Seattle topology conference [Lashof1965].
which are not isotopic to the identity. We give such a construction which probably goes back to Milnor: so far the earliest reference found is the problem list of the 1963 Seattle topology conference [Lashof1965].
Represent 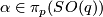 and
and 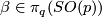 by smooth compactly supported functions
by smooth compactly supported functions 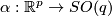 and
and 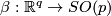 and define the following self-diffeomorphisms of
and define the following self-diffeomorphisms of 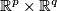
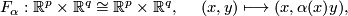
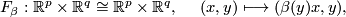
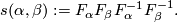
If follows that 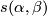 is compactly supported and so extends uniquely to a diffeomrphism of
is compactly supported and so extends uniquely to a diffeomrphism of  . In this way we obtain a bilinear pairing
. In this way we obtain a bilinear pairing
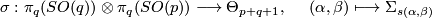
such that
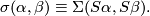
In particular 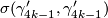 generates
generates  for
for 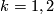 .
.
3 Invariants
Signature, Kervaire invariant,  -invariant, Eels-Kuiper invariant,
-invariant, Eels-Kuiper invariant,  -invariant.
-invariant.
4 Classification
For  , group of exotic spheres
, group of exotic spheres  fits into the following long exact sequence which stops at
fits into the following long exact sequence which stops at 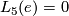 :
:
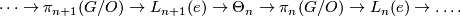
The existence of the above sequence was proven in [Kervaire&Milnor1963]. More details can also be found in [Levine1983].
5 Further discussion
![\displaystyle \def\curv{1.5pc}% Adjust the curvature of the curved arrows here \xymatrix@!R@!C@!0@R=2.5pc@C=4pc{% Adjust the spacing here \pi_n(\Top/O) \ar[dr] \ar@/u\curv/[rr] && \pi_{n-1}(O) \ar[dr] \ar@/u\curv/[rr] && \pi_{n-1}(G) \\ & \pi_n(G/O) \ar[dr] \ar[ur] && \pi_{n-1}(\Top) \ar[dr] \ar[ur] \\ \pi_n(G) \ar[ur] \ar@/d\curv/[rr] && \pi_n(G/\Top) \ar[ur] \ar@/d\curv/[rr] && \pi_{n-1}(\Top/O) }](/images/math/8/3/2/8329c4c4fce71895022bc3e0ed9b9b7b.png)
6 External references
- Wikipedia article on exotic spheres
- http://www.maths.ed.ac.uk/~aar/exotic.htm Andrew Ranicki's exotic sphere home page, with many of the original papers.
7 References
- [Adams1958] J. F. Adams, On the nonexistence of elements of Hopf invariant one, Bull. Amer. Math. Soc. 64 (1958), 279–282. MR0097059 (20 #3539) Zbl 0178.26106
- [Adams1960] J. F. Adams, On the non-existence of elements of Hopf invariant one, Ann. of Math. (2) 72 (1960), 20–104. MR0141119 (25 #4530) Zbl 0096.17404
- [Cerf1970] J. Cerf, La stratification naturelle des espaces de fonctions différentiables réelles et le théorème de la pseudo-isotopie, Inst. Hautes Études Sci. Publ. Math. (1970), no.39, 5–173. MR0292089 (45 #1176) Zbl 0213.25202
- [Eells&Kuiper1962] J. Eells and N. Kuiper, An invariant for certain smooth manifolds, Ann. Mat. Pura Appl. (4) 60 (1962), 93–110. MR0156356 (27 #6280) Zbl 0119.18704
- [Freedman1982] M. H. Freedman, The topology of four-dimensional manifolds, J. Differential Geom. 17 (1982), no.3, 357–453. MR679066 (84b:57006) Zbl 0528.57011
- [Kervaire&Milnor1963] M. A. Kervaire and J. W. Milnor, Groups of homotopy spheres. I, Ann. of Math. (2) 77 (1963), 504–537. MR0148075 (26 #5584) Zbl 0115.40505
- [Lashof1965] R. Lashof, Problems in differential and algebraic topology. Seattle Conference, 1963, Ann. of Math. (2) 81 (1965), 565–591. MR0182961 (32 #443) Zbl 0137.17601
- [Levine1983] J. P. Levine, Lectures on groups of homotopy spheres, Algebraic and geometric topology (New Brunswick, N.J., 1983), Lecture Notes in Math., 1126 (1983), 62–95. MR802786 (87i:57031) Zbl 0576.57028
- [Milnor1956] J. Milnor, On manifolds homeomorphic to the
 -sphere, Ann. of Math. (2) 64 (1956), 399–405. MR0082103 (18,498d) Zbl 0072.18402
-sphere, Ann. of Math. (2) 64 (1956), 399–405. MR0082103 (18,498d) Zbl 0072.18402
- [Milnor1959] J. Milnor, Differentiable structures on spheres, Amer. J. Math. 81 (1959), 962–972. MR0110107 (22 #990) Zbl 0111.35501
- [Shimada1957] N. Shimada, Differentiable structures on the 15-sphere and Pontrjagin classes of certain manifolds, Nagoya Math. J. 12 (1957), 59–69. MR0096223 (20 #2715) Zbl 0145.20303
- [Smale1962a] S. Smale, On the structure of manifolds, Amer. J. Math. 84 (1962), 387–399. MR0153022 (27 #2991) Zbl 0109.41103
- [Wall1962] C. T. C. Wall, Killing the middle homotopy groups of odd dimensional manifolds, Trans. Amer. Math. Soc. 103 (1962), 421–433. MR0139185 (25 #2621) Zbl 0199.26803