Elementary matricies (Ex)
Let 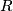 be an associative ring with unit and recall that an elementary matrix
be an associative ring with unit and recall that an elementary matrix  over
over 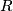 is a square matrix of the form
is a square matrix of the form
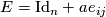
where 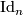 is the
is the 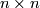 identity matrix,
identity matrix, 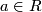 and
and 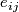 is the matrix with zeros in all places except
is the matrix with zeros in all places except 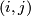 where it is
where it is  and we have
and we have 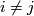 . Clearly each elementary matrix is invertible and so defines an element
. Clearly each elementary matrix is invertible and so defines an element 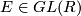 where
where
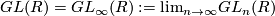
is the limit of the invertible matricies.
Exercise 0.1.
Prove that ![E(R)=[GL(R),GL(R)]](/images/math/a/2/a/a2ac3f81c640b9978b9ad187c7af1875.png) , where
, where 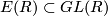 is the subgroup generated by all elements in
is the subgroup generated by all elements in 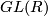 which are represented by elementary matrices.
which are represented by elementary matrices.
Hint 0.2.
For 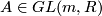 and
and 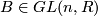 write the matrix
write the matrix
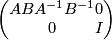
as a product of elementary matrices
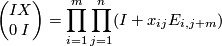
where 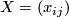 is an
is an 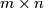 matrix.
matrix.
Recall that 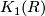 is defined to be the abelian group
is defined to be the abelian group
![\displaystyle K_1(R) : = GL(R)_{ab} = GL(R)/[GL(R), GL(R)].](/images/math/a/5/0/a50f6109d26038e574733fb869dbd3a6.png)
Exercise 0.3.
Prove that 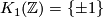 .
.
 over
over 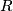 is a square matrix of the form
is a square matrix of the form
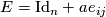
where 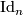 is the
is the 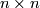 identity matrix,
identity matrix, 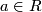 and
and 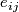 is the matrix with zeros in all places except
is the matrix with zeros in all places except 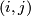 where it is
where it is  and we have
and we have 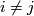 . Clearly each elementary matrix is invertible and so defines an element
. Clearly each elementary matrix is invertible and so defines an element 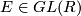 where
where
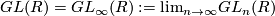
is the limit of the invertible matricies.
Exercise 0.1.
Prove that ![E(R)=[GL(R),GL(R)]](/images/math/a/2/a/a2ac3f81c640b9978b9ad187c7af1875.png) , where
, where 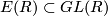 is the subgroup generated by all elements in
is the subgroup generated by all elements in 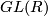 which are represented by elementary matrices.
which are represented by elementary matrices.
Hint 0.2.
For 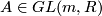 and
and 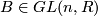 write the matrix
write the matrix
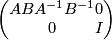
as a product of elementary matrices
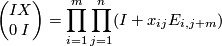
where 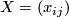 is an
is an 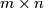 matrix.
matrix.
Recall that 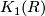 is defined to be the abelian group
is defined to be the abelian group
![\displaystyle K_1(R) : = GL(R)_{ab} = GL(R)/[GL(R), GL(R)].](/images/math/a/5/0/a50f6109d26038e574733fb869dbd3a6.png)
Exercise 0.3.
Prove that 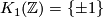 .
.