Dynamics of foliations
|
The user responsible for this page is Pawel Walczak. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Foliations of Riemannian manifolds can be considered as multidimensional dynamical systems: Riemannian structure (more precisely, Riemannian structure along the leaves) plays the role of time, the leaves play the role of orbits [Walczak2004]. The dynamics of a foliation can be described in terms of its holonomy (see Foliations#Holonomy) pseudogroup. As far as we know, the notion of a pseudogroup appeared for the first time in [Veblen&Whitehead1932] in the context of geometric objects studied in differential geometry. Pseudogroups have been brought into the foliation theory by Haefliger [Haefliger1962a]. The growth types of leaves (equivalent to the growth types of the corresponding orbits of holonomy pseudogroups) as well as the expansion growth of a foliation (or, its holonomy pseudogroup) describe some aspects of the foliation dynamics. Corresponding to the expansion growth is the notion of geometric entropy of a foliation [Ghys&Langevin&Walczak1988]. Vanishing entropy can be seen as a dynamical condition which occurs to have strong geometric and topological consequences (see Dynamics of foliations#Results on entropy) below.
2 Pseudogroups
The notion of a pseudogroup generalizes that of a group of
transformations. Given a space  , any group of transformations of
, any group of transformations of  consists of maps defined globally on
consists of maps defined globally on  , mapping
, mapping  bijectively onto
itself and such that the composition of any two of them as well as the
inverse of any of them belongs to the group. The same holds for a
pseudogroup with this difference that the maps are not defined globally
but on open subsets, so the domain of the composition is usually smaller
than those of the maps being composed.
bijectively onto
itself and such that the composition of any two of them as well as the
inverse of any of them belongs to the group. The same holds for a
pseudogroup with this difference that the maps are not defined globally
but on open subsets, so the domain of the composition is usually smaller
than those of the maps being composed.
To make the above precise, let us take a topological space  and denote
by Homeo
and denote
by Homeo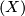 the family of all
homeomorphisms between open subsets of
the family of all
homeomorphisms between open subsets of  . If
. If 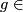 Homeo
Homeo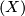 , then
, then
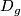 is its domain and
is its domain and 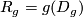 .
.
Definition 2.1.
A subfamily 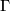 of Homeo
of Homeo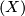 is said to be a pseudogroup
if it
is closed under composition, inversion, restriction to open subdomains and
unions. More precisely,
is said to be a pseudogroup
if it
is closed under composition, inversion, restriction to open subdomains and
unions. More precisely, 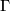 should satisfy the following conditions:
should satisfy the following conditions:
(i) 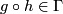 whenever
whenever  and
and 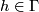 ,
,
(ii) 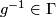 whenever
whenever 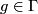 ,
,
(iii) 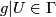 whenever
whenever 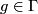 and
and 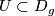 is
open,
is
open,
(iv) if 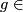 Homeo
Homeo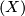 ,
, 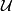 is an open cover of
is an open cover of 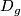 and
and
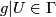 for any
for any 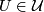 , then
, then 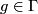 .
.
Moreover, we shall always assume that
(v] id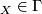 (or, equivalently,
(or, equivalently, 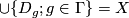 ).
).
As examples, one may have (1) all the homeomorphisms between open sets of a topological space, (2) all the diffeomorhisms of a given class (say, 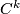 ,
, 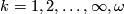 , between open sets of a manifold, (3) all the restrictions to open domains of elements of a given group
, between open sets of a manifold, (3) all the restrictions to open domains of elements of a given group  of homeomorphisms of a given topological space. (In the last case, we say that the pseudogroup is generated by
of homeomorphisms of a given topological space. (In the last case, we say that the pseudogroup is generated by  .)
Any set
.)
Any set  of homeomorphisms bewteen open sets (with domains covering a space
of homeomorphisms bewteen open sets (with domains covering a space  ) generates ma pseudogroup
) generates ma pseudogroup 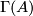 which is the smallest pseudogroup containing
which is the smallest pseudogroup containing  ; precisely a homeomorphism
; precisely a homeomorphism 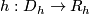 belongs to
belongs to 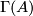 if and only if for any point
if and only if for any point 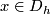 there exist elements
there exist elements 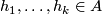 , exponents
, exponents 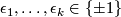 and a neighbourhood
and a neighbourhood  of
of  such that
such that 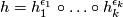 on
on  . If
. If  is finite,
is finite, 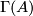 is said to be finitely generated.
is said to be finitely generated.
3 Holonomy pesudogroups
Definition 3.1. A foliated atlas 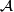 on a foliated manifold
on a foliated manifold 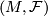 is said to be
nice (also, nice is the
covering of
is said to be
nice (also, nice is the
covering of  by the domains
by the domains 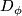 of the charts
of the charts 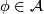 ) if
) if
(i) the covering 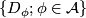 is locally finite,
is locally finite,
(ii) for any 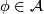 ,
, 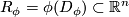 is an open cube,
is an open cube,
(iii) if  and
and 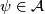 , and
, and 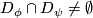 ,
then there exists a foliated chart chart
,
then there exists a foliated chart chart 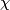 and such that
and such that
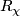 is an open cube,
is an open cube, 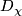 contains the closure of
contains the closure of 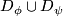 and
and 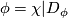 .
.
Since manifolds are supposed to be paracompact here, they are separable and hence nice coverings are denumerable. Nice coverings on compact manifolds are finite. On arbitrary foliated manfiolds, nice coverings do exist.
Given a nice covering 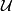 of a foliated manifold
of a foliated manifold 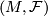 . For
any
. For
any 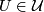 , let
, let 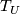 be the space of the plaques (i.e., connected components of intersections
be the space of the plaques (i.e., connected components of intersections  .
.  being a leaf of
being a leaf of  ) of
) of  contained in
contained in  . Equip
. Equip 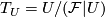 with the quotient topology: two points of
with the quotient topology: two points of
 are equivalent iff they belong to the same plaque.
are equivalent iff they belong to the same plaque. 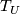 is homeomorphic
(
is homeomorphic
( -diffeomorphic when
-diffeomorphic when  is
is  -differentiable and
-differentiable and 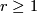 ) to an
open cube
) to an
open cube 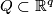 (
(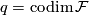 ) via the map
) via the map
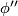 , where
, where 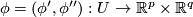 is a foliated chart on
is a foliated chart on  .
The disjoint union
.
The disjoint union
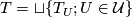
is called a complete transversal for  . Transversality refers to the fact that, if
. Transversality refers to the fact that, if  is differentiable of class
is differentiable of class  ,
,  , each of the spaces
, each of the spaces 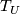 can be mapped homeomorphically onto a
can be mapped homeomorphically onto a  -submanifold
-submanifold 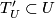 transverse to
transverse to  : if
: if 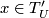 and
and  is the leaf of
is the leaf of  passing through
passing through  ,
then
,
then
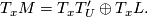
Completeness of  means that every leaf of
means that every leaf of  intersects at least one
of the submanifolds
intersects at least one
of the submanifolds 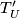 .
.
Definition 3.2. Given a nice covering 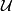 of a foliated manifold
of a foliated manifold 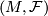 and two sets
and two sets  and
and 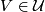 such that
such that 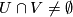 the holonomy map
the holonomy map 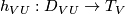 ,
,
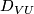 being the open subset of
being the open subset of 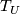 which consists of all the plaques
which consists of all the plaques
 of
of  for which
for which 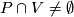 , is defined in the following
way:
, is defined in the following
way:
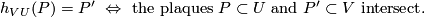
All the maps 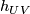 (
(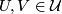 ) generate a pseudogroup
) generate a pseudogroup 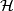 on
on  .
.
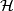 is called the holonomy pseudogroup of
is called the holonomy pseudogroup of  .
.
This means that any element of 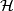 assigns to a plaque
assigns to a plaque  the end plaque
the end plaque 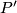 of a chain (that is a sequence of plaques such that any two consequtive plaques intersect) which oroginates at
of a chain (that is a sequence of plaques such that any two consequtive plaques intersect) which oroginates at  .
.
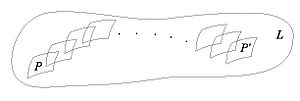
Certainly, holonomy pseudogroups of arbitrary compact foliated manifolds are finitely generated. For example, gluing together two 2-dimensional Reeb foliations (see Foliations#Reeb Foliations) on 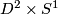 one gets a foliation of the 3-dimensional sphere
one gets a foliation of the 3-dimensional sphere  for which any arc
for which any arc  intersecting the unique toral leaf
intersecting the unique toral leaf 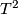 is a complete transversal;
is a complete transversal;  can be identified with a segment
can be identified with a segment 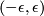 (
( ), the point of intersection
), the point of intersection 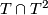 with the number
with the number  , while the holonomy group with the one on our segment generated by two maps
, while the holonomy group with the one on our segment generated by two maps 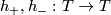 such that
such that 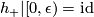 ,
, ![h_-|(-\epsilon , 0] = \id](/images/math/1/9/9/19940d575c63343d81d296a0ce65a779.png) ,
, ![h_+|(-\epsilon , 0]](/images/math/3/3/7/337ac03b439e1bb6a54a4a90ce882bce.png) snd
snd 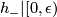 contract their domains towards
contract their domains towards  .
.
4 Growth
5 Geometric entropy
6 Invariant measures
7 Results on entropy
8 References
- [Ghys&Langevin&Walczak1988] É. Ghys, R. Langevin and P. Walczak, Entropie géométrique des feuilletages, Acta Math. 160 (1988), no.1-2, 105–142. MR926526 (89a:57034) Zbl 0666.57021
- [Haefliger1962a] A. Haefliger, Variétés feuilletées, Ann. Scuola Norm. Sup. Pisa (3) 16 (1962), 367–397. MR0189060 (32 #6487) Zbl 0196.25005
- [Veblen&Whitehead1932] O. Veblen and J. Whitehead, The foundations of differential geometry, Cambridge Tracts in Math. a. Math. Phys. 29) London: Cambridge Univ. Press. IX, 97 S., 1932. Zbl 0005.21801
- [Walczak2004] P. Walczak, Dynamics of foliations, groups and pseudogroups, Birkhäuser Verlag, 2004. MR2056374 (2005d:57042) Zbl 1084.37022
 consists of maps defined globally on
consists of maps defined globally on  , mapping
, mapping  bijectively onto
itself and such that the composition of any two of them as well as the
inverse of any of them belongs to the group. The same holds for a
pseudogroup with this difference that the maps are not defined globally
but on open subsets, so the domain of the composition is usually smaller
than those of the maps being composed.
bijectively onto
itself and such that the composition of any two of them as well as the
inverse of any of them belongs to the group. The same holds for a
pseudogroup with this difference that the maps are not defined globally
but on open subsets, so the domain of the composition is usually smaller
than those of the maps being composed.
To make the above precise, let us take a topological space  and denote
by Homeo
and denote
by Homeo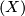 the family of all
homeomorphisms between open subsets of
the family of all
homeomorphisms between open subsets of  . If
. If 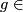 Homeo
Homeo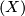 , then
, then
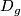 is its domain and
is its domain and 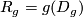 .
.
Definition 2.1.
A subfamily 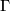 of Homeo
of Homeo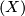 is said to be a pseudogroup
if it
is closed under composition, inversion, restriction to open subdomains and
unions. More precisely,
is said to be a pseudogroup
if it
is closed under composition, inversion, restriction to open subdomains and
unions. More precisely, 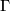 should satisfy the following conditions:
should satisfy the following conditions:
(i) 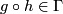 whenever
whenever  and
and 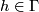 ,
,
(ii) 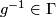 whenever
whenever 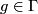 ,
,
(iii) 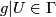 whenever
whenever 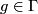 and
and 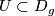 is
open,
is
open,
(iv) if 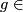 Homeo
Homeo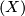 ,
, 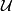 is an open cover of
is an open cover of 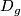 and
and
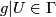 for any
for any 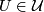 , then
, then 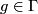 .
.
Moreover, we shall always assume that
(v] id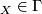 (or, equivalently,
(or, equivalently, 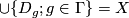 ).
).
As examples, one may have (1) all the homeomorphisms between open sets of a topological space, (2) all the diffeomorhisms of a given class (say, 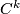 ,
, 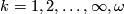 , between open sets of a manifold, (3) all the restrictions to open domains of elements of a given group
, between open sets of a manifold, (3) all the restrictions to open domains of elements of a given group  of homeomorphisms of a given topological space. (In the last case, we say that the pseudogroup is generated by
of homeomorphisms of a given topological space. (In the last case, we say that the pseudogroup is generated by  .)
Any set
.)
Any set  of homeomorphisms bewteen open sets (with domains covering a space
of homeomorphisms bewteen open sets (with domains covering a space  ) generates ma pseudogroup
) generates ma pseudogroup 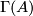 which is the smallest pseudogroup containing
which is the smallest pseudogroup containing  ; precisely a homeomorphism
; precisely a homeomorphism 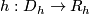 belongs to
belongs to 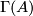 if and only if for any point
if and only if for any point 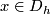 there exist elements
there exist elements 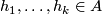 , exponents
, exponents 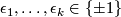 and a neighbourhood
and a neighbourhood  of
of  such that
such that 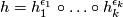 on
on  . If
. If  is finite,
is finite, 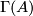 is said to be finitely generated.
is said to be finitely generated.
3 Holonomy pesudogroups
Definition 3.1. A foliated atlas 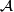 on a foliated manifold
on a foliated manifold 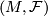 is said to be
nice (also, nice is the
covering of
is said to be
nice (also, nice is the
covering of  by the domains
by the domains 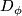 of the charts
of the charts 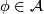 ) if
) if
(i) the covering 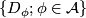 is locally finite,
is locally finite,
(ii) for any 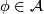 ,
, 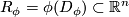 is an open cube,
is an open cube,
(iii) if  and
and 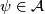 , and
, and 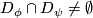 ,
then there exists a foliated chart chart
,
then there exists a foliated chart chart 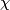 and such that
and such that
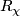 is an open cube,
is an open cube, 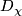 contains the closure of
contains the closure of 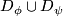 and
and 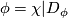 .
.
Since manifolds are supposed to be paracompact here, they are separable and hence nice coverings are denumerable. Nice coverings on compact manifolds are finite. On arbitrary foliated manfiolds, nice coverings do exist.
Given a nice covering 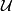 of a foliated manifold
of a foliated manifold 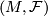 . For
any
. For
any 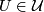 , let
, let 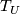 be the space of the plaques (i.e., connected components of intersections
be the space of the plaques (i.e., connected components of intersections  .
.  being a leaf of
being a leaf of  ) of
) of  contained in
contained in  . Equip
. Equip 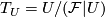 with the quotient topology: two points of
with the quotient topology: two points of
 are equivalent iff they belong to the same plaque.
are equivalent iff they belong to the same plaque. 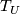 is homeomorphic
(
is homeomorphic
( -diffeomorphic when
-diffeomorphic when  is
is  -differentiable and
-differentiable and 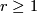 ) to an
open cube
) to an
open cube 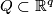 (
(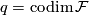 ) via the map
) via the map
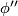 , where
, where 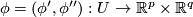 is a foliated chart on
is a foliated chart on  .
The disjoint union
.
The disjoint union
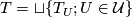
is called a complete transversal for  . Transversality refers to the fact that, if
. Transversality refers to the fact that, if  is differentiable of class
is differentiable of class  ,
,  , each of the spaces
, each of the spaces 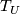 can be mapped homeomorphically onto a
can be mapped homeomorphically onto a  -submanifold
-submanifold 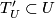 transverse to
transverse to  : if
: if 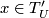 and
and  is the leaf of
is the leaf of  passing through
passing through  ,
then
,
then
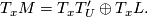
Completeness of  means that every leaf of
means that every leaf of  intersects at least one
of the submanifolds
intersects at least one
of the submanifolds 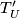 .
.
Definition 3.2. Given a nice covering 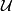 of a foliated manifold
of a foliated manifold 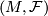 and two sets
and two sets  and
and 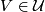 such that
such that 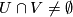 the holonomy map
the holonomy map 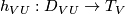 ,
,
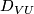 being the open subset of
being the open subset of 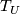 which consists of all the plaques
which consists of all the plaques
 of
of  for which
for which 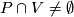 , is defined in the following
way:
, is defined in the following
way:
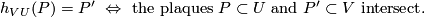
All the maps 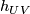 (
(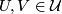 ) generate a pseudogroup
) generate a pseudogroup 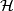 on
on  .
.
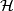 is called the holonomy pseudogroup of
is called the holonomy pseudogroup of  .
.
This means that any element of 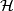 assigns to a plaque
assigns to a plaque  the end plaque
the end plaque 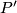 of a chain (that is a sequence of plaques such that any two consequtive plaques intersect) which oroginates at
of a chain (that is a sequence of plaques such that any two consequtive plaques intersect) which oroginates at  .
.
Certainly, holonomy pseudogroups of arbitrary compact foliated manifolds are finitely generated. For example, gluing together two 2-dimensional Reeb foliations (see Foliations#Reeb Foliations) on 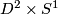 one gets a foliation of the 3-dimensional sphere
one gets a foliation of the 3-dimensional sphere  for which any arc
for which any arc  intersecting the unique toral leaf
intersecting the unique toral leaf 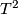 is a complete transversal;
is a complete transversal;  can be identified with a segment
can be identified with a segment 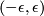 (
( ), the point of intersection
), the point of intersection 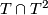 with the number
with the number  , while the holonomy group with the one on our segment generated by two maps
, while the holonomy group with the one on our segment generated by two maps 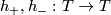 such that
such that 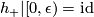 ,
, ![h_-|(-\epsilon , 0] = \id](/images/math/1/9/9/19940d575c63343d81d296a0ce65a779.png) ,
, ![h_+|(-\epsilon , 0]](/images/math/3/3/7/337ac03b439e1bb6a54a4a90ce882bce.png) snd
snd 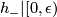 contract their domains towards
contract their domains towards  .
.
4 Growth
5 Geometric entropy
6 Invariant measures
7 Results on entropy
8 References
- [Ghys&Langevin&Walczak1988] É. Ghys, R. Langevin and P. Walczak, Entropie géométrique des feuilletages, Acta Math. 160 (1988), no.1-2, 105–142. MR926526 (89a:57034) Zbl 0666.57021
- [Haefliger1962a] A. Haefliger, Variétés feuilletées, Ann. Scuola Norm. Sup. Pisa (3) 16 (1962), 367–397. MR0189060 (32 #6487) Zbl 0196.25005
- [Veblen&Whitehead1932] O. Veblen and J. Whitehead, The foundations of differential geometry, Cambridge Tracts in Math. a. Math. Phys. 29) London: Cambridge Univ. Press. IX, 97 S., 1932. Zbl 0005.21801
- [Walczak2004] P. Walczak, Dynamics of foliations, groups and pseudogroups, Birkhäuser Verlag, 2004. MR2056374 (2005d:57042) Zbl 1084.37022
 consists of maps defined globally on
consists of maps defined globally on  , mapping
, mapping  bijectively onto
itself and such that the composition of any two of them as well as the
inverse of any of them belongs to the group. The same holds for a
pseudogroup with this difference that the maps are not defined globally
but on open subsets, so the domain of the composition is usually smaller
than those of the maps being composed.
bijectively onto
itself and such that the composition of any two of them as well as the
inverse of any of them belongs to the group. The same holds for a
pseudogroup with this difference that the maps are not defined globally
but on open subsets, so the domain of the composition is usually smaller
than those of the maps being composed.
To make the above precise, let us take a topological space  and denote
by Homeo
and denote
by Homeo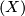 the family of all
homeomorphisms between open subsets of
the family of all
homeomorphisms between open subsets of  . If
. If 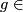 Homeo
Homeo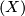 , then
, then
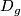 is its domain and
is its domain and 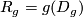 .
.
Definition 2.1.
A subfamily 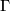 of Homeo
of Homeo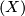 is said to be a pseudogroup
if it
is closed under composition, inversion, restriction to open subdomains and
unions. More precisely,
is said to be a pseudogroup
if it
is closed under composition, inversion, restriction to open subdomains and
unions. More precisely, 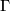 should satisfy the following conditions:
should satisfy the following conditions:
(i) 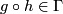 whenever
whenever  and
and 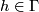 ,
,
(ii) 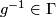 whenever
whenever 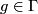 ,
,
(iii) 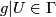 whenever
whenever 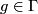 and
and 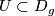 is
open,
is
open,
(iv) if 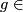 Homeo
Homeo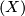 ,
, 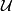 is an open cover of
is an open cover of 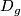 and
and
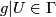 for any
for any 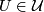 , then
, then 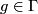 .
.
Moreover, we shall always assume that
(v] id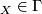 (or, equivalently,
(or, equivalently, 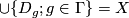 ).
).
As examples, one may have (1) all the homeomorphisms between open sets of a topological space, (2) all the diffeomorhisms of a given class (say, 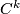 ,
, 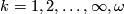 , between open sets of a manifold, (3) all the restrictions to open domains of elements of a given group
, between open sets of a manifold, (3) all the restrictions to open domains of elements of a given group  of homeomorphisms of a given topological space. (In the last case, we say that the pseudogroup is generated by
of homeomorphisms of a given topological space. (In the last case, we say that the pseudogroup is generated by  .)
Any set
.)
Any set  of homeomorphisms bewteen open sets (with domains covering a space
of homeomorphisms bewteen open sets (with domains covering a space  ) generates ma pseudogroup
) generates ma pseudogroup 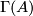 which is the smallest pseudogroup containing
which is the smallest pseudogroup containing  ; precisely a homeomorphism
; precisely a homeomorphism 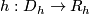 belongs to
belongs to 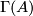 if and only if for any point
if and only if for any point 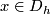 there exist elements
there exist elements 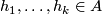 , exponents
, exponents 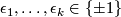 and a neighbourhood
and a neighbourhood  of
of  such that
such that 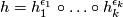 on
on  . If
. If  is finite,
is finite, 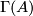 is said to be finitely generated.
is said to be finitely generated.
3 Holonomy pesudogroups
Definition 3.1. A foliated atlas 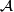 on a foliated manifold
on a foliated manifold 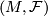 is said to be
nice (also, nice is the
covering of
is said to be
nice (also, nice is the
covering of  by the domains
by the domains 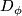 of the charts
of the charts 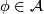 ) if
) if
(i) the covering 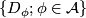 is locally finite,
is locally finite,
(ii) for any 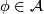 ,
, 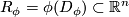 is an open cube,
is an open cube,
(iii) if  and
and 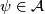 , and
, and 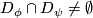 ,
then there exists a foliated chart chart
,
then there exists a foliated chart chart 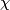 and such that
and such that
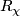 is an open cube,
is an open cube, 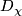 contains the closure of
contains the closure of 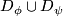 and
and 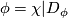 .
.
Since manifolds are supposed to be paracompact here, they are separable and hence nice coverings are denumerable. Nice coverings on compact manifolds are finite. On arbitrary foliated manfiolds, nice coverings do exist.
Given a nice covering 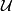 of a foliated manifold
of a foliated manifold 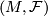 . For
any
. For
any 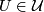 , let
, let 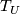 be the space of the plaques (i.e., connected components of intersections
be the space of the plaques (i.e., connected components of intersections  .
.  being a leaf of
being a leaf of  ) of
) of  contained in
contained in  . Equip
. Equip 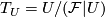 with the quotient topology: two points of
with the quotient topology: two points of
 are equivalent iff they belong to the same plaque.
are equivalent iff they belong to the same plaque. 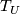 is homeomorphic
(
is homeomorphic
( -diffeomorphic when
-diffeomorphic when  is
is  -differentiable and
-differentiable and 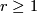 ) to an
open cube
) to an
open cube 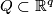 (
(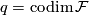 ) via the map
) via the map
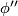 , where
, where 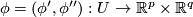 is a foliated chart on
is a foliated chart on  .
The disjoint union
.
The disjoint union
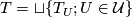
is called a complete transversal for  . Transversality refers to the fact that, if
. Transversality refers to the fact that, if  is differentiable of class
is differentiable of class  ,
,  , each of the spaces
, each of the spaces 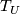 can be mapped homeomorphically onto a
can be mapped homeomorphically onto a  -submanifold
-submanifold 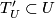 transverse to
transverse to  : if
: if 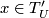 and
and  is the leaf of
is the leaf of  passing through
passing through  ,
then
,
then
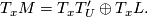
Completeness of  means that every leaf of
means that every leaf of  intersects at least one
of the submanifolds
intersects at least one
of the submanifolds 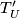 .
.
Definition 3.2. Given a nice covering 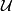 of a foliated manifold
of a foliated manifold 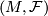 and two sets
and two sets  and
and 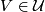 such that
such that 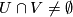 the holonomy map
the holonomy map 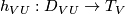 ,
,
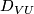 being the open subset of
being the open subset of 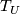 which consists of all the plaques
which consists of all the plaques
 of
of  for which
for which 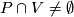 , is defined in the following
way:
, is defined in the following
way:
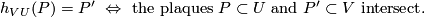
All the maps 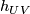 (
(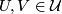 ) generate a pseudogroup
) generate a pseudogroup 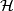 on
on  .
.
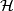 is called the holonomy pseudogroup of
is called the holonomy pseudogroup of  .
.
This means that any element of 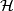 assigns to a plaque
assigns to a plaque  the end plaque
the end plaque 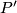 of a chain (that is a sequence of plaques such that any two consequtive plaques intersect) which oroginates at
of a chain (that is a sequence of plaques such that any two consequtive plaques intersect) which oroginates at  .
.
Certainly, holonomy pseudogroups of arbitrary compact foliated manifolds are finitely generated. For example, gluing together two 2-dimensional Reeb foliations (see Foliations#Reeb Foliations) on 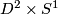 one gets a foliation of the 3-dimensional sphere
one gets a foliation of the 3-dimensional sphere  for which any arc
for which any arc  intersecting the unique toral leaf
intersecting the unique toral leaf 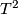 is a complete transversal;
is a complete transversal;  can be identified with a segment
can be identified with a segment 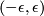 (
( ), the point of intersection
), the point of intersection 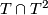 with the number
with the number  , while the holonomy group with the one on our segment generated by two maps
, while the holonomy group with the one on our segment generated by two maps 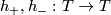 such that
such that 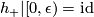 ,
, ![h_-|(-\epsilon , 0] = \id](/images/math/1/9/9/19940d575c63343d81d296a0ce65a779.png) ,
, ![h_+|(-\epsilon , 0]](/images/math/3/3/7/337ac03b439e1bb6a54a4a90ce882bce.png) snd
snd 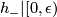 contract their domains towards
contract their domains towards  .
.
4 Growth
5 Geometric entropy
6 Invariant measures
7 Results on entropy
8 References
- [Ghys&Langevin&Walczak1988] É. Ghys, R. Langevin and P. Walczak, Entropie géométrique des feuilletages, Acta Math. 160 (1988), no.1-2, 105–142. MR926526 (89a:57034) Zbl 0666.57021
- [Haefliger1962a] A. Haefliger, Variétés feuilletées, Ann. Scuola Norm. Sup. Pisa (3) 16 (1962), 367–397. MR0189060 (32 #6487) Zbl 0196.25005
- [Veblen&Whitehead1932] O. Veblen and J. Whitehead, The foundations of differential geometry, Cambridge Tracts in Math. a. Math. Phys. 29) London: Cambridge Univ. Press. IX, 97 S., 1932. Zbl 0005.21801
- [Walczak2004] P. Walczak, Dynamics of foliations, groups and pseudogroups, Birkhäuser Verlag, 2004. MR2056374 (2005d:57042) Zbl 1084.37022