Dynamics of foliations
|
The user responsible for this page is Pawel Walczak. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Introduction
Foliations of Riemannian manifolds can be considered as multidimensional dynamical systems: Riemannian structure (more precisely, Riemannian structure along the leaves) plays the role of time, the leaves play the role of orbits [Walczak2004]. The dynamics of a foliation can be described in terms of its holonomy psudogroup (see Foliations#Holonomy).
2 Pseudogroups
The notion of a pseudogroup generalizes that of a group of
transformations. Given a space  , any group of transformations of
, any group of transformations of  consists of maps defined globally on
consists of maps defined globally on  , mapping
, mapping  bijectively onto
itself and such that the composition of any two of them as well as the
inverse of any of them belongs to the group. The same holds for a
pseudogroup with this difference that the maps are not defined globally
but on open subsets, so the domain of the composition is usually smaller
than those of the maps being composed.
bijectively onto
itself and such that the composition of any two of them as well as the
inverse of any of them belongs to the group. The same holds for a
pseudogroup with this difference that the maps are not defined globally
but on open subsets, so the domain of the composition is usually smaller
than those of the maps being composed.
To make the above precise, let us take a topological space  and denote
by Homeo
and denote
by Homeo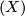 the family of all
homeomorphisms between open subsets of
the family of all
homeomorphisms between open subsets of  . If
. If 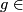 Homeo
Homeo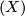 , then
, then
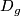 is its domain and
is its domain and 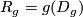 .
.
Definition 2.1.
A subfamily  of Homeo
of Homeo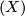 is said to be a pseudogroup
if it
is closed under composition, inversion, restriction to open subdomains and
unions. More precisely,
is said to be a pseudogroup
if it
is closed under composition, inversion, restriction to open subdomains and
unions. More precisely,  should satisfy the following conditions:
should satisfy the following conditions:
(i) 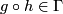 whenever
whenever  and
and 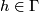 ,
,
(ii) 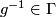 whenever
whenever 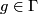 ,
,
(iii) 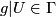 whenever
whenever 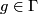 and
and 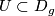 is
open,
is
open,
(iv) if 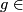 Homeo
Homeo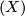 ,
, 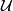 is an open cover of
is an open cover of 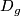 and
and
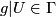 for any
for any 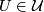 , then
, then 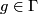 .
.
Moreover, we shall always assume that
(v] id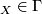 (or, equivalently,
(or, equivalently, 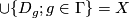 ).
).
As examples, one may have (1) all the homeomorphisms between open sets of a topological space, (2) all the diffeomorhisms of a given class (say, C$^k$, $k = 1, 2, \ldots, \infty, \omega$, between open sets of a manifold, (3) all the restrictions to open domains of elements of a given group $G$ of homeomorphisms of a given topological space. (In the last case, we say that the pseudogroup is generated by $G$.) Any set $A$ of homeomorphisms bewteen open sets (with domains covering a space $X$) generates ma pseudogroup $\Gamma (A)$ which is the smallest pseudogroup containing $A$; precisely a homeomorphism $h\D_h\to R_h$ belongs to $\Gamma (A)$ if and only if for any point $x\in D_h$ there exist elements $h_1, \ldots, h_k\in A$, exponents $\epsilon _1, \ldots, \epsilon _k\n\{ \pm 1\}$ and a neighbourhood $V$ of $x$ such that $h = h_1^{\epsilon _1}\circ\ldots\circ h_k^{\]epsilon _k}$ on $V$.
3 References
- [Walczak2004] P. Walczak, Dynamics of foliations, groups and pseudogroups, Birkhäuser Verlag, 2004. MR2056374 (2005d:57042) Zbl 1084.37022