Does the existence of a string structure depend on a spin structure ? (and a generalization)
(→References) |
|||
| Line 33: | Line 33: | ||
on the spin structure. | on the spin structure. | ||
| − | The answer is however yes for larger $n$. For example the existence of a $BO\langle 9\rangle$-structure on a string vector bundle | + | The answer is however yes for all larger $n$ with $BO\langle n\rangle\ne BO\langle n+1\rangle$. |
| − | can depend on the string structure. | + | For example the existence of a $BO\langle 9\rangle$-structure on a string vector bundle can depend on the string structure. |
| + | |||
</wikitex> | </wikitex> | ||
| Line 42: | Line 43: | ||
$$\Omega K(\pi_{n}BO,n) \to PK(\pi_{n}BO,n) \to K(\pi_{n}BO,n)$$ via a map $BO\langle n\rangle \to K(\pi_{n}BO,n)$, corresponding to a class $k\in H^{n}(BO\langle n\rangle;\pi_{n}BO)$. Note that this is the generator of $H^{n}(BO\langle n\rangle;\pi_{n}BO)\cong Hom(\pi_{n}BO;\pi_{n}BO)$. | $$\Omega K(\pi_{n}BO,n) \to PK(\pi_{n}BO,n) \to K(\pi_{n}BO,n)$$ via a map $BO\langle n\rangle \to K(\pi_{n}BO,n)$, corresponding to a class $k\in H^{n}(BO\langle n\rangle;\pi_{n}BO)$. Note that this is the generator of $H^{n}(BO\langle n\rangle;\pi_{n}BO)\cong Hom(\pi_{n}BO;\pi_{n}BO)$. | ||
| + | In the case $n=4i$, it follows from [[Obstruction_classes_and_Pontryagin_classes|this result]] | ||
| + | that the Pontryagin class $p_i\in H^{4i}(BO;\Zz)$ maps to a certain multiple | ||
| + | $b_i\cdot k\in H^{4i}(BO\langle 4i\rangle;\Zz)$ (see [[Obstruction_classes_and_Pontryagin_classes|here]] for the value of $b_i$). | ||
| + | In these cases, the generator $k$ is usally denoted by $\frac{p_i}{b_i}$, although | ||
| + | $p_i\in H^{4i}(BO;\Zz)$ itself is indivisible. | ||
| + | |||
By obstruction theory, it follows that a map $f:X\to BO\langle n \rangle$ lifts to $BO\langle n+1\rangle$ if and only if the "characteristic" class | By obstruction theory, it follows that a map $f:X\to BO\langle n \rangle$ lifts to $BO\langle n+1\rangle$ if and only if the "characteristic" class | ||
$$f^*k\in H^{n}(X;\pi_{n}BO)$$ vanishes. | $$f^*k\in H^{n}(X;\pi_{n}BO)$$ vanishes. | ||
This is for $n=1,2$ the first and second Stiefel-Whitney class of the corresponding vector bundle over $X$. | This is for $n=1,2$ the first and second Stiefel-Whitney class of the corresponding vector bundle over $X$. | ||
In particular, since the Stiefel-Whitney classes of a vector bundle are independent of an orientation, this answers the question for $n=2$. | In particular, since the Stiefel-Whitney classes of a vector bundle are independent of an orientation, this answers the question for $n=2$. | ||
| + | |||
| + | For every $BO\langle n\rangle$-structure on a vector bundle $X\to BO$ there exists an opposite $BO\langle n\rangle$-structure (inducing the opposite orientation) defined as follows: | ||
| + | The connective cover construction is functorial, thus the non-trivial deck transformation $\tau$ | ||
| + | of the $2$-fold cover $BSO\to BO$ induces a self-map $\tau$ of $BO\langle n\rangle$. | ||
| + | Composing the $BO\langle n\rangle$-structure with this self-map of $BO\langle n\rangle$ gives the opposite structure. | ||
| + | We have $\tau^*(k)=k$ since $\tau$ is a self-equivalence which for $n=4k$ is the identity on the Pontryagin classes. | ||
| + | Thus for a $BO\langle n\rangle$-structure and its opposite, either both lift to a $BO\langle n+1\rangle$-structure | ||
| + | or both do not. | ||
| + | |||
In general, we are given two maps $f,g:X\to BO\langle n \rangle$ (i.e. two stable vector bundles over $X$ with $BO\langle n \rangle$-structure) | In general, we are given two maps $f,g:X\to BO\langle n \rangle$ (i.e. two stable vector bundles over $X$ with $BO\langle n \rangle$-structure) | ||
| Line 67: | Line 83: | ||
For $n=4,m=2$ we need to know the pullback of $k=\frac{p_1}{2}$ under $i: K(\Zz_2,1)\to BSpin$. | For $n=4,m=2$ we need to know the pullback of $k=\frac{p_1}{2}$ under $i: K(\Zz_2,1)\to BSpin$. | ||
| − | This is zero. | + | This is zero, since the reduction modulo $2$ is trivial, as the reduction of $k$ modulo $2$ is the image of $w_4\in H^4(BO;\Zz_2)$. See {{cite|Stong1963|p.539}}. |
| + | |||
| + | For higher $n,m$ we show that $i^*(k)\ne 0$ by considering reductions modulo $p$, which have been computed | ||
| + | for $p=2$ by {{cite|Stong1963}} and for $p$ odd by {{cite|Giambalvo1969}}. | ||
For $n=8,m=4$ we need to know the pullback of $k=\frac{p_2}{6}$ under $i: K(\Zz,3)\to BString$. | For $n=8,m=4$ we need to know the pullback of $k=\frac{p_2}{6}$ under $i: K(\Zz,3)\to BString$. | ||
| − | This is a non-zero class: it suffices to show that its reduction modulo 3 is nontrivial. | + | This is a non-zero class: it suffices to show that its reduction modulo $3$ is nontrivial. |
| − | This follows from {{cite|Giambalvo1969|Theorem 1'}}. | + | This follows from {{cite|Giambalvo1969|Theorem 1'}}. (The reduction modulo $2$ of $k$ is $w_8$, |
| + | so that the reduction modulo $2$ of $i^*k$ is zero.) | ||
Thus for example the trivial stable vector bundle on $K(\Zz,3)$ admits a string structure which does not lift to a $BO\langle 9\rangle$-structure. | Thus for example the trivial stable vector bundle on $K(\Zz,3)$ admits a string structure which does not lift to a $BO\langle 9\rangle$-structure. | ||
| − | + | In all higher dimensions $n$, the (reductions modulo $2$ of) $i^*k$ are non-zero by {{cite|Stong1963|p.539}}. | |
</wikitex> | </wikitex> | ||
Revision as of 17:01, 21 January 2011
Contents |
1 Question
Let 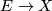 be a (stable) vector bundle. This has a classifying map
be a (stable) vector bundle. This has a classifying map 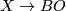 .
.
A 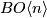 -structure on
-structure on  is (the vertical homotopy class of) a lift of the classifying map to a map
is (the vertical homotopy class of) a lift of the classifying map to a map 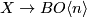 .
(For
.
(For 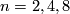 this is an orientation, a spin structure, a string structure respectively.)
this is an orientation, a spin structure, a string structure respectively.)
Since for 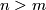 ,the map
,the map 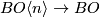 factors through
factors through
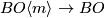 , a
, a 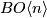 -structure induces a
-structure induces a 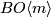 -structure, or, vice versa,
this specific
-structure, or, vice versa,
this specific 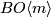 -structure can be lifted to a
-structure can be lifted to a 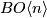 -structure.
-structure.
Question 1.1.
Given a vector bundle 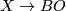 and two
and two 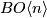 -structures on it,
is it possible that one of the
-structures on it,
is it possible that one of the 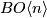 -structures can be lifted to a
-structures can be lifted to a 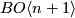 -structure and the other can't?
-structure and the other can't?
2 Answers
This is not possible for  and
and 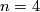 , i.e. the question whether an oriented vector bundle admits a spin structure
does not depend on the orientation, and the question whether a spin vector bundle admits a string structure does not depend
on the spin structure.
, i.e. the question whether an oriented vector bundle admits a spin structure
does not depend on the orientation, and the question whether a spin vector bundle admits a string structure does not depend
on the spin structure.
The answer is however yes for all larger  with
with 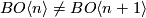 .
For example the existence of a
.
For example the existence of a 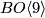 -structure on a string vector bundle can depend on the string structure.
-structure on a string vector bundle can depend on the string structure.
3 Further discussion
The map 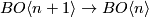 has homotopy fiber
has homotopy fiber 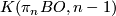 and is the pullback of the path-loop fibration
and is the pullback of the path-loop fibration
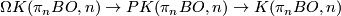
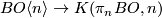 , corresponding to a class
, corresponding to a class 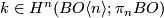 . Note that this is the generator of
. Note that this is the generator of 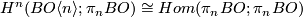 .
.
In the case 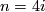 , it follows from this result
that the Pontryagin class
, it follows from this result
that the Pontryagin class 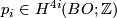 maps to a certain multiple
maps to a certain multiple
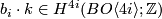 (see here for the value of
(see here for the value of 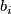 ).
In these cases, the generator
).
In these cases, the generator  is usally denoted by
is usally denoted by 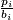 , although
, although
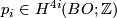 itself is indivisible.
itself is indivisible.
By obstruction theory, it follows that a map 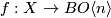 lifts to
lifts to 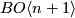 if and only if the "characteristic" class
if and only if the "characteristic" class
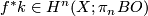
This is for 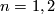 the first and second Stiefel-Whitney class of the corresponding vector bundle over
the first and second Stiefel-Whitney class of the corresponding vector bundle over  .
In particular, since the Stiefel-Whitney classes of a vector bundle are independent of an orientation, this answers the question for
.
In particular, since the Stiefel-Whitney classes of a vector bundle are independent of an orientation, this answers the question for  .
.
For every 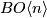 -structure on a vector bundle
-structure on a vector bundle 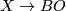 there exists an opposite
there exists an opposite 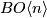 -structure (inducing the opposite orientation) defined as follows:
The connective cover construction is functorial, thus the non-trivial deck transformation
-structure (inducing the opposite orientation) defined as follows:
The connective cover construction is functorial, thus the non-trivial deck transformation  of the
of the  -fold cover
-fold cover 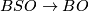 induces a self-map
induces a self-map  of
of 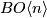 .
Composing the
.
Composing the 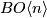 -structure with this self-map of
-structure with this self-map of 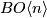 gives the opposite structure.
We have
gives the opposite structure.
We have 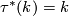 since
since  is a self-equivalence which for
is a self-equivalence which for 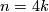 is the identity on the Pontryagin classes.
Thus for a
is the identity on the Pontryagin classes.
Thus for a 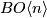 -structure and its opposite, either both lift to a
-structure and its opposite, either both lift to a 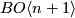 -structure
or both do not.
-structure
or both do not.
In general, we are given two maps 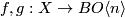 (i.e. two stable vector bundles over
(i.e. two stable vector bundles over  with
with 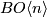 -structure)
for which we assume that the compositions with
-structure)
for which we assume that the compositions with 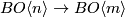 are homotopic
(i.e. the bundles are isomorphic as bundles with
are homotopic
(i.e. the bundles are isomorphic as bundles with 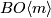 -structure).
We have to investigate whether it is possible that
-structure).
We have to investigate whether it is possible that 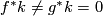 .
Here let us assume that
.
Here let us assume that 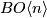 and
and 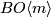 are consecutive connective covers in the sense that
are consecutive connective covers in the sense that
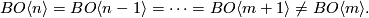
Since the compositions of  and
and  with
with 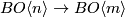 are homotopic, it follows that
are homotopic, it follows that  and
and  differ by a map
from
differ by a map
from  to the homotopy fiber
to the homotopy fiber 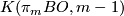 of
of 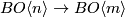 .
More precisely, the map
.
More precisely, the map 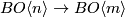 is a map of H-spaces, and given
is a map of H-spaces, and given 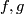 as above, there exists
a map
as above, there exists
a map 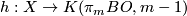 such that
such that  is homotopic to the composition
is homotopic to the composition
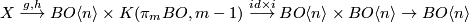
where the last map is the  -space multiplication.
-space multiplication.
Under the  -space multiplication
-space multiplication  pulls back to
pulls back to
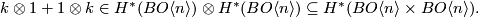
Now it follows that 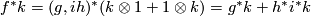 .
.
Now we choose 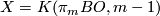 and
and 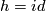 as the "universal" example; thus we have to know whether
as the "universal" example; thus we have to know whether 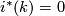 .
.
For 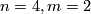 we need to know the pullback of
we need to know the pullback of 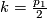 under
under 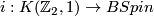 .
This is zero, since the reduction modulo
.
This is zero, since the reduction modulo  is trivial, as the reduction of
is trivial, as the reduction of  modulo
modulo  is the image of
is the image of 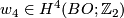 . See [Stong1963, p.539].
. See [Stong1963, p.539].
For higher 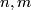 we show that
we show that 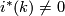 by considering reductions modulo
by considering reductions modulo  , which have been computed
for
, which have been computed
for 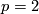 by [Stong1963] and for
by [Stong1963] and for  odd by [Giambalvo1969].
odd by [Giambalvo1969].
For 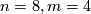 we need to know the pullback of
we need to know the pullback of 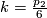 under
under 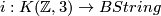 .
This is a non-zero class: it suffices to show that its reduction modulo
.
This is a non-zero class: it suffices to show that its reduction modulo  is nontrivial.
This follows from [Giambalvo1969, Theorem 1']. (The reduction modulo
is nontrivial.
This follows from [Giambalvo1969, Theorem 1']. (The reduction modulo  of
of  is
is 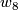 ,
so that the reduction modulo
,
so that the reduction modulo  of
of 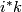 is zero.)
is zero.)
Thus for example the trivial stable vector bundle on 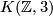 admits a string structure which does not lift to a
admits a string structure which does not lift to a 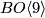 -structure.
-structure.
In all higher dimensions  , the (reductions modulo
, the (reductions modulo  of)
of) 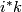 are non-zero by [Stong1963, p.539].
are non-zero by [Stong1963, p.539].
4 References
- [Giambalvo1969] V. Giambalvo, The
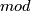
 cohomology of
cohomology of 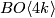 , Proc. Amer. Math. Soc. 20 (1969), 593–597. MR0236913 (38 #5206) Zbl 0176.52601
, Proc. Amer. Math. Soc. 20 (1969), 593–597. MR0236913 (38 #5206) Zbl 0176.52601
- [Stong1963] R. E. Stong, Determination of
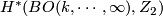 and
and 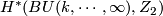 , Trans. Amer. Math. Soc. 107 (1963), 526–544. MR0151963 (27 #1944) Zbl 0116.14702
, Trans. Amer. Math. Soc. 107 (1963), 526–544. MR0151963 (27 #1944) Zbl 0116.14702