Does the existence of a string structure depend on a spin structure ? (and a generalization)
(Created page with "<!-- COMMENT: To achieve a unified layout, along with using the template below, please OBSERVE the following: besides, $...$ and $$...$$, you should use two environments: - Fo...") |
|||
| Line 51: | Line 51: | ||
In general, we are given two maps $f,g:X\to BO\langle n \rangle$ (i.e. two stable vector bundles over $X$ with $BO\langle n \rangle$-structure) | In general, we are given two maps $f,g:X\to BO\langle n \rangle$ (i.e. two stable vector bundles over $X$ with $BO\langle n \rangle$-structure) | ||
for which we assume that the compositions with $BO\langle n \rangle \to BO\langle m \rangle$ are homotopic | for which we assume that the compositions with $BO\langle n \rangle \to BO\langle m \rangle$ are homotopic | ||
| − | (i.e. the bundles are isomorphic as bundles with $BO\langle | + | (i.e. the bundles are isomorphic as bundles with $BO\langle m \rangle$-structure). |
We have to investigate whether it is possible that $f^*k\ne g^*k=0$. | We have to investigate whether it is possible that $f^*k\ne g^*k=0$. | ||
Here let us assume that $BO\langle n\rangle$ and $BO\langle m\rangle$ are consecutive connective covers in the sense that | Here let us assume that $BO\langle n\rangle$ and $BO\langle m\rangle$ are consecutive connective covers in the sense that | ||
Revision as of 18:49, 20 January 2011
Contents |
1 Question
Let 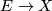 be a (stable) vector bundle. This has a classifying map
be a (stable) vector bundle. This has a classifying map 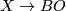 .
.
A 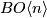 -structure on
-structure on  is (the vertical homotopy class of) a lift of the classifying map to a map
is (the vertical homotopy class of) a lift of the classifying map to a map 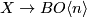 .
(For
.
(For 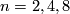 this is an orientation, a spin structure, a string structure respectively.)
this is an orientation, a spin structure, a string structure respectively.)
Since for 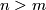 ,the map
,the map 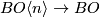 factors through
factors through
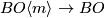 , a
, a 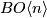 -structure induces a
-structure induces a 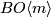 -structure, or, vice versa,
this specific
-structure, or, vice versa,
this specific 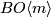 -structure can be lifted to a
-structure can be lifted to a 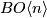 -structure.
-structure.
Question 1.1.
Given a vector bundle 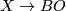 and two
and two 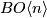 -structures on it,
is it possible that one of the
-structures on it,
is it possible that one of the 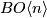 -structures can be lifted to a
-structures can be lifted to a 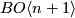 -structure and the other can't?
-structure and the other can't?
2 Answers
This is not possible for  and
and 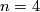 , i.e. the question whether an oriented vector bundle admits a spin structure
does not depend on the orientation, and the question whether a spin vector bundle admits a string structure does not depend
on the spin structure.
, i.e. the question whether an oriented vector bundle admits a spin structure
does not depend on the orientation, and the question whether a spin vector bundle admits a string structure does not depend
on the spin structure.
The answer is however yes for larger  . For example the existence of a
. For example the existence of a 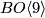 -structure on a string vector bundle
can depend on the string structure.
-structure on a string vector bundle
can depend on the string structure.
3 Further discussion
The map 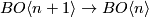 has homotopy fiber
has homotopy fiber 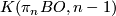 and is the pullback of the path-loop fibration
and is the pullback of the path-loop fibration
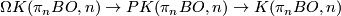
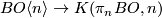 , corresponding to a class
, corresponding to a class 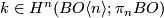 . Note that this is the generator of
. Note that this is the generator of 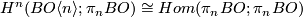 .
.
By obstruction theory, it follows that a map 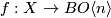 lifts to
lifts to 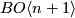 if and only if the "characteristic" class
if and only if the "characteristic" class
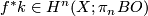
This is for 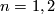 the first and second Stiefel-Whitney class of the corresponding vector bundle over
the first and second Stiefel-Whitney class of the corresponding vector bundle over  .
In particular, since the Stiefel-Whitney classes of a vector bundle are independent of an orientation, this answers the question for
.
In particular, since the Stiefel-Whitney classes of a vector bundle are independent of an orientation, this answers the question for  .
.
In general, we are given two maps 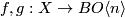 (i.e. two stable vector bundles over
(i.e. two stable vector bundles over  with
with 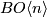 -structure)
for which we assume that the compositions with
-structure)
for which we assume that the compositions with 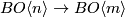 are homotopic
(i.e. the bundles are isomorphic as bundles with
are homotopic
(i.e. the bundles are isomorphic as bundles with 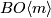 -structure).
We have to investigate whether it is possible that
-structure).
We have to investigate whether it is possible that 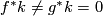 .
Here let us assume that
.
Here let us assume that 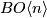 and
and 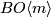 are consecutive connective covers in the sense that
are consecutive connective covers in the sense that
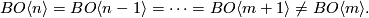
Since the compositions of  and
and  with
with 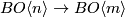 are homotopic, it follows that
are homotopic, it follows that  and
and  differ by a map
from
differ by a map
from  to the homotopy fiber
to the homotopy fiber 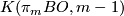 of
of 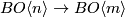 .
More precisely, the map
.
More precisely, the map 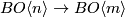 is a map of H-spaces, and given
is a map of H-spaces, and given 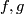 as above, there exists
a map
as above, there exists
a map 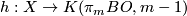 such that
such that  is homotopic to the composition
is homotopic to the composition
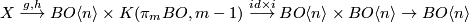
where the last map is the  -space multiplication.
-space multiplication.
Under the  -space multiplication
-space multiplication  pulls back to
pulls back to
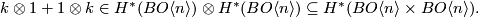
Now it follows that 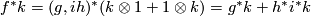 .
.
Now we choose 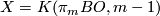 and
and 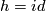 as the "universal" example; thus we have to know whether
as the "universal" example; thus we have to know whether 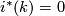 .
.
For 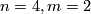 we need to know the pullback of
we need to know the pullback of 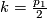 under
under 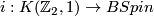 .
This is zero.
.
This is zero.
For 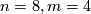 we need to know the pullback of
we need to know the pullback of 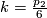 under
under 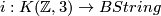 .
This is a non-zero class: it suffices to show that its reduction modulo 3 is nontrivial.
This follows from [Giambalvo1969, Theorem 1'].
.
This is a non-zero class: it suffices to show that its reduction modulo 3 is nontrivial.
This follows from [Giambalvo1969, Theorem 1'].
4 References
- [Giambalvo1969] V. Giambalvo, The
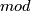
 cohomology of
cohomology of 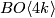 , Proc. Amer. Math. Soc. 20 (1969), 593–597. MR0236913 (38 #5206) Zbl 0176.52601
, Proc. Amer. Math. Soc. 20 (1969), 593–597. MR0236913 (38 #5206) Zbl 0176.52601