Dehn surgery (Ex)
From Manifold Atlas
(Difference between revisions)
(Created page with "<wikitex>; ... </wikitex> == References == {{#RefList:}} Category:Exercises Category:Exercises without solution") |
|||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | ... | + | Let $K$ be an embedded $S^1\hookrightarrow S^3$ with a closed tubular neighbourhood $\nu K \cong S^1 \times D^2$. A '''Dehn surgery''' on $K$ is the process of removing int$(\nu K)$ and gluing back in a copy of $S^1\times D^2$ by any diffeomorphism $$\phi: S^1\times \partial D^2 \to \partial\nu K$$ of the boundary tori. Orienting $K$, let $\alpha$ be a right-handed meridean and $\beta\in H_1(\partial\nu K; \Z)$ a $0$-framed copy of $K$ pushed to the boundary of $\nu K$. A Lens space $L(p,-q)$ is defined to be the effect of Dehn surgery on the standard embedding $S^1\hookrightarrow S^3$ with $\phi$ such that $$\phi_*([\partial D^2]) = p\alpha + q\beta.$$ |
| + | '''1)''' Show $L(\pm 2, 1) \simeq \R P^3$, $L(\pm 1, 1) = L(p,0) = S^3$. | ||
| + | |||
| + | '''2)''' Prove the `slam dunk' - that the combined effect of the two surgeries on the Hopf link in $S^3$ with framings $m$ and $n$ on the respective components is the Lens space $L(1-mn,n)$. Hence show that any Lens space is null-cobordant. | ||
| + | |||
| + | '''Hint:''' It may help to prove that $L(p,-q) = L(-p,q)$ so that we can unambiguously consider the Dehn surgery generating the space as `$p/q$-surgery' on the embedded $S^1$. | ||
| + | |||
</wikitex> | </wikitex> | ||
== References == | == References == | ||
Latest revision as of 21:07, 25 August 2013
 be an embedded
be an embedded 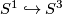 with a closed tubular neighbourhood
with a closed tubular neighbourhood 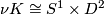 . A Dehn surgery on
. A Dehn surgery on  is the process of removing int
is the process of removing int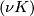 and gluing back in a copy of
and gluing back in a copy of 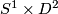 by any diffeomorphism
by any diffeomorphism 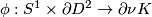
 , let
, let  be a right-handed meridean and
be a right-handed meridean and 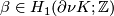 a
a  -framed copy of
-framed copy of  pushed to the boundary of
pushed to the boundary of 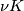 . A Lens space
. A Lens space 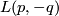 is defined to be the effect of Dehn surgery on the standard embedding
is defined to be the effect of Dehn surgery on the standard embedding 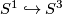 with
with  such that
such that ![\displaystyle \phi_*([\partial D^2]) = p\alpha + q\beta.](/images/math/a/0/6/a06d067dbaa9efd35595811c8a200809.png)
1) Show 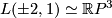 ,
, 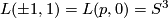 .
.
2) Prove the `slam dunk' - that the combined effect of the two surgeries on the Hopf link in  with framings
with framings  and
and  on the respective components is the Lens space
on the respective components is the Lens space 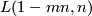 . Hence show that any Lens space is null-cobordant.
. Hence show that any Lens space is null-cobordant.
Hint: It may help to prove that 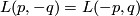 so that we can unambiguously consider the Dehn surgery generating the space as `
so that we can unambiguously consider the Dehn surgery generating the space as `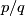 -surgery' on the embedded
-surgery' on the embedded  .
.
References
$-framed copy of $K$ pushed to the boundary of $\nu K$. A Lens space $L(p,-q)$ is defined to be the effect of Dehn surgery on the standard embedding $S^1\hookrightarrow S^3$ with $\phi$ such that $$\phi_*([\partial D^2]) = p\alpha + q\beta.$$ '''1)''' Show $L(\pm 2, 1) \simeq \R P^3$, $L(\pm 1, 1) = L(p,0) = S^3$. '''2)''' Prove the `slam dunk' - that the combined effect of the two surgeries on the Hopf link in $S^3$ with framings $m$ and $n$ on the respective components is the Lens space $L(1-mn,n)$. Hence show that any Lens space is null-cobordant. '''Hint:''' It may help to prove that $L(p,-q) = L(-p,q)$ so that we can unambiguously consider the Dehn surgery generating the space as `$p/q$-surgery' on the embedded $S^1$. == References == {{#RefList:}} [[Category:Exercises]] [[Category:Exercises without solution]]K be an embedded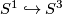 with a closed tubular neighbourhood
with a closed tubular neighbourhood 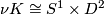 . A Dehn surgery on
. A Dehn surgery on  is the process of removing int
is the process of removing int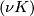 and gluing back in a copy of
and gluing back in a copy of 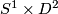 by any diffeomorphism
by any diffeomorphism 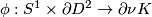
 , let
, let  be a right-handed meridean and
be a right-handed meridean and 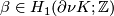 a
a  -framed copy of
-framed copy of  pushed to the boundary of
pushed to the boundary of 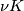 . A Lens space
. A Lens space 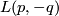 is defined to be the effect of Dehn surgery on the standard embedding
is defined to be the effect of Dehn surgery on the standard embedding 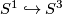 with
with  such that
such that ![\displaystyle \phi_*([\partial D^2]) = p\alpha + q\beta.](/images/math/a/0/6/a06d067dbaa9efd35595811c8a200809.png)
1) Show 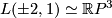 ,
, 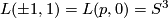 .
.
2) Prove the `slam dunk' - that the combined effect of the two surgeries on the Hopf link in  with framings
with framings  and
and  on the respective components is the Lens space
on the respective components is the Lens space 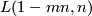 . Hence show that any Lens space is null-cobordant.
. Hence show that any Lens space is null-cobordant.
Hint: It may help to prove that 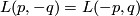 so that we can unambiguously consider the Dehn surgery generating the space as `
so that we can unambiguously consider the Dehn surgery generating the space as `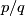 -surgery' on the embedded
-surgery' on the embedded  .
.