Connected sum
m (→Introduction) |
|||
| Line 1: | Line 1: | ||
{{Stub}} | {{Stub}} | ||
| − | == | + | == Connected sum of smooth manifolds == |
<wikitex>; | <wikitex>; | ||
| − | Let $M$ be a compact connected n-manifold with base point $m \in \mathrm{int} M$. Recall that that a local orientation for $M$ is a choice of orientation of $TM_m$, the tangent space to $M$ at $m$. We write $-M$ for $M$ with the opposition orientation at $m$. Of course, if $M$ is orientable then a local orientation for $M$ defines an orientation on $M$. | + | <!-- Let $M$ be a compact connected n-manifold with base point $m \in \mathrm{int} M$. Recall that that a local orientation for $M$ is a choice of orientation of $TM_m$, the tangent space to $M$ at $m$. We write $-M$ for $M$ with the opposition orientation at $m$. Of course, if $M$ is orientable then a local orientation for $M$ defines an orientation on $M$. |
If $M$ and $N$ are locally oriented n-manifolds then their [[Wikipedia:Connected_sum|connected sum]] is defined by | If $M$ and $N$ are locally oriented n-manifolds then their [[Wikipedia:Connected_sum|connected sum]] is defined by | ||
$$ M \sharp N = ((M - m) \cup (N - n))/ \simeq$$ | $$ M \sharp N = ((M - m) \cup (N - n))/ \simeq$$ | ||
| − | where $\simeq$ is defined using the local orientations to identify small balls about $m$ and $n$. The diffeomorphism type of $M \sharp N$ is well-defined: in fact $M \sharp N$ is the outcome of 0-surgery on $M \sqcup N$. The essential point is \cite{Hirsch} which states, for any $M$ and any two compatibly oriented embeddings $ | + | where $\simeq$ is defined using the local orientations to identify small balls about $m$ and $n$. The diffeomorphism type of $M \sharp N$ is well-defined: in fact $M \sharp N$ is the outcome of 0-surgery on $M \sqcup N$. The essential point is \cite{Hirsch} which states, for any $M$ and any two compatibly oriented embeddings $f_1: D^n \to M$ and $f_1 : D^n \to M$, that $f_0$ is isotopic to $f_1$. --> |
| + | Let $M_0$ and $M_1$ be oriented closed smooth connected $n$-manifolds. Their connected sum is an oriented closed smooth connected $n$-manifold | ||
| + | \[ M_1 \sharp M_2 \] | ||
| + | which is defined as follows (c.f. \cite{Kervaire&Milnor1963|Section 2}. Choose smooth embeddings | ||
| + | \[ i_0 \colon D^n \to M_0 \quad \text{and} \quad i_1 \colon D^n \to M_1 \] | ||
| + | where $i_1$ preserves orientations and $i_2$ reverses orientations. The connected sum is formed from the | ||
| + | disjoint union | ||
| + | \[ (M_0 - i_0(0)) \sqcup (M_1 - i_1(0) \] | ||
| + | by identifying $i_0(tu)$ with $i_1((1-t)u)$ for $u \in S^{n-1}$ and $0 < t < 1$. The smooth structure on | ||
| + | $M_0 \sharp M_1$ is obtain from the charts on $M_0 - i_0(0)$ and $M_1 - i_1(0)$. The orientation on | ||
| + | $M_0 \sharp M_1$ is chosen to be the one compatible with the orientation of $M_0$ and $M_1$. | ||
| − | If $M$ and $N$ are oriented manifolds the connected sum $M \sharp N$ is a well-defined up to diffeomorphism. Note that orientation matters! The | + | A fundamental lemma of differential topology, \cite{Palais1959|Theorem 5.5} \cite{Cerf1961} states that any |
| + | two orientation preserving smootgh embeddings of the $n$-disc into a closed oriented smooth $n$-manifold are isotopic. As a consequence we have the following lemma. | ||
| + | |||
| + | {{beginthm|Lemma|\cite{Kervaire&Milnor1963|Lemma 2.1}}} | ||
| + | The connected sum operation is well defined, associative and commutative up to | ||
| + | orientation preserving diffeomoprhism. The sphere $S^n$ serves as the identity element. | ||
| + | {{endthm}} | ||
| + | |||
| + | The connected sum operation also descends to give well-defined operations on larger equivalence classes | ||
| + | of oriented manifolds. | ||
| + | |||
| + | {{beginthm|Lemma|c.f. \cite{Kervaire&Milnor1963|Lemma 2.2}}}} | ||
| + | Let $M_0$, $M_0'$ and $M_1$ be oriented closed connected smooth manifold. Suppose that $M_0$ is [[h-cobordism|h-cobordant]] to $M_0'$, resp. bordant to $M_0'$ then $M_0 \sharp M_1$ is h-cobordant, resp. bordant, to $M_0' \sharp M_1$. | ||
| + | {{endthm}} | ||
| + | <!-- If $M$ and $N$ are oriented manifolds the connected sum $M \sharp N$ is a well-defined up to diffeomorphism. Note that orientation matters! --> | ||
| + | == Exmaples== | ||
| + | The orientation of the manifolds is important in general. The canonical example is | ||
$$ \CP^2 \sharp \CP^2 \neq \CP^2 \sharp (-\CP^2).$$ | $$ \CP^2 \sharp \CP^2 \neq \CP^2 \sharp (-\CP^2).$$ | ||
The manifolds are not even homotopy equivalent: the first has signature 2 the other signature 0. The following elementary lemma is often useful to remember. | The manifolds are not even homotopy equivalent: the first has signature 2 the other signature 0. The following elementary lemma is often useful to remember. | ||
| − | |||
{{beginthm|Lemma}} | {{beginthm|Lemma}} | ||
Let $M$ and $N$ be locally oriented manifolds such that there is a diffeomoprhism $N \cong -N$, then $M \sharp N \cong M \sharp (-N)$. | Let $M$ and $N$ be locally oriented manifolds such that there is a diffeomoprhism $N \cong -N$, then $M \sharp N \cong M \sharp (-N)$. | ||
{{endthm}} | {{endthm}} | ||
| + | |||
| + | Connected sum decompositions of manifolds are far from being unique. For example, let $M = S^3 \tilde \times S^4$ be the total space of the non-trivial 3-sphere bundle over $S^4$ with Euler class zero and Pontrjagin class four times a preferred generator of $H^4(S^4; \Z) \cong \Z$. | ||
| + | {{beginthm|Lemma|c.f.\cite{Wilkens1974/75|Theorem 1} }} | ||
| + | There are diffeomorphisms | ||
| + | # $M \sharp M \cong M \sharp (S^3 \times S^4)$ | ||
| + | # $M \sharp \Sigma \cong M$ for any homotopy sphere $\Sigma$. (Recall that the | ||
| + | group of [[Exotic spheres|homotopy 7-spheres]], $\Theta_7$ is isomorphic to $\Z/28$.) | ||
| + | {{endthm}} | ||
| + | {{beginproof}} | ||
| + | 1.) | ||
| + | |||
| + | 2.) From | ||
| + | {{endproof}} | ||
| + | |||
| + | |||
| + | |||
| + | |||
</wikitex> | </wikitex> | ||
Revision as of 17:11, 21 February 2013
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Connected sum of smooth manifolds
Let  and
and  be oriented closed smooth connected
be oriented closed smooth connected  -manifolds. Their connected sum is an oriented closed smooth connected
-manifolds. Their connected sum is an oriented closed smooth connected  -manifold
\[ M_1 \sharp M_2 \]
which is defined as follows (c.f. [Kervaire&Milnor1963, Section 2]. Choose smooth embeddings
\[ i_0 \colon D^n \to M_0 \quad \text{and} \quad i_1 \colon D^n \to M_1 \]
where
-manifold
\[ M_1 \sharp M_2 \]
which is defined as follows (c.f. [Kervaire&Milnor1963, Section 2]. Choose smooth embeddings
\[ i_0 \colon D^n \to M_0 \quad \text{and} \quad i_1 \colon D^n \to M_1 \]
where 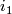 preserves orientations and
preserves orientations and 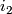 reverses orientations. The connected sum is formed from the
disjoint union
\[ (M_0 - i_0(0)) \sqcup (M_1 - i_1(0) \]
by identifying
reverses orientations. The connected sum is formed from the
disjoint union
\[ (M_0 - i_0(0)) \sqcup (M_1 - i_1(0) \]
by identifying 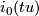 with
with 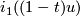 for
for 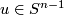 and
and 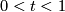 . The smooth structure on
. The smooth structure on
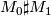 is obtain from the charts on
is obtain from the charts on 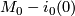 and
and 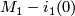 . The orientation on
. The orientation on
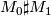 is chosen to be the one compatible with the orientation of
is chosen to be the one compatible with the orientation of  and
and  .
.
A fundamental lemma of differential topology, [Palais1959, Theorem 5.5] [Cerf1961] states that any
two orientation preserving smootgh embeddings of the  -disc into a closed oriented smooth
-disc into a closed oriented smooth  -manifold are isotopic. As a consequence we have the following lemma.
-manifold are isotopic. As a consequence we have the following lemma.
Lemma 1.1 [Kervaire&Milnor1963, Lemma 2.1].
The connected sum operation is well defined, associative and commutative up to
orientation preserving diffeomoprhism. The sphere  serves as the identity element.
serves as the identity element.
The connected sum operation also descends to give well-defined operations on larger equivalence classes of oriented manifolds.
Lemma 1.2 c.f. [Kervaire&Milnor1963, Lemma 2.2].}
Let  ,
, 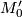 and
and  be oriented closed connected smooth manifold. Suppose that
be oriented closed connected smooth manifold. Suppose that  is h-cobordant to
is h-cobordant to 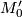 , resp. bordant to
, resp. bordant to 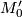 then
then 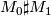 is h-cobordant, resp. bordant, to
is h-cobordant, resp. bordant, to 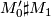 .
.
Exmaples
The orientation of the manifolds is important in general. The canonical example is
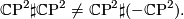
The manifolds are not even homotopy equivalent: the first has signature 2 the other signature 0. The following elementary lemma is often useful to remember.
Lemma 3.1.
Let  and
and  be locally oriented manifolds such that there is a diffeomoprhism
be locally oriented manifolds such that there is a diffeomoprhism 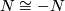 , then
, then 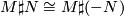 .
.
Connected sum decompositions of manifolds are far from being unique. For example, let 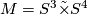 be the total space of the non-trivial 3-sphere bundle over
be the total space of the non-trivial 3-sphere bundle over  with Euler class zero and Pontrjagin class four times a preferred generator of
with Euler class zero and Pontrjagin class four times a preferred generator of 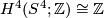 .
.
Lemma 3.2 c.f.[Wilkens1974/75, Theorem 1] . There are diffeomorphisms
-
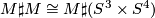
-
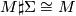 for any homotopy sphere
for any homotopy sphere  . (Recall that the
. (Recall that the
group of homotopy 7-spheres, 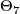 is isomorphic to
is isomorphic to 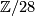 .)
.)
Proof. 1.)
2.) From

2 References
- [Cerf1961] J. Cerf, Topologie de certains espaces de plongements, Bull. Soc. Math. France 89 (1961), 227–380. MR0140120 (25 #3543) Zbl 0101.16001
- [Kervaire&Milnor1963] M. A. Kervaire and J. W. Milnor, Groups of homotopy spheres. I, Ann. of Math. (2) 77 (1963), 504–537. MR0148075 (26 #5584) Zbl 0115.40505
- [Palais1959] R. S. Palais, Natural operations on differential forms, Trans. Amer. Math. Soc. 92 (1959), 125–141. MR0116352 (22 #7140) Zbl 0092.30802
- [Wilkens1974/75] D. L. Wilkens, On the inertia groups of certain manifolds, J. London Math. Soc. (2) 9 (1974/75), 537–548. MR0383435 (52 #4316)