Connected sum
m |
|||
| Line 19: | Line 19: | ||
== References == | == References == | ||
{{#RefList:}} | {{#RefList:}} | ||
| + | |||
| + | == External links == | ||
| + | * [http://mathoverflow.net/questions/121571/connected-sum-of-topological-manifolds Mathoverflow:Connected sum of topological manifolds] | ||
[[Category:Theory]] | [[Category:Theory]] | ||
[[Category:Definitions]] | [[Category:Definitions]] | ||
Revision as of 15:59, 21 February 2013
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Introduction
Let  be a compact connected n-manifold with base point
be a compact connected n-manifold with base point 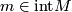 . Recall that that a local orientation for
. Recall that that a local orientation for  is a choice of orientation of
is a choice of orientation of 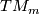 , the tangent space to
, the tangent space to  at
at  . We write
. We write 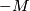 for
for  with the opposition orientation at
with the opposition orientation at  . Of course, if
. Of course, if  is orientable then a local orientation for
is orientable then a local orientation for  defines an orientation on
defines an orientation on  .
.
If  and
and  are locally oriented n-manifolds then their connected sum is defined by
are locally oriented n-manifolds then their connected sum is defined by
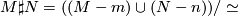
where 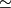 is defined using the local orientations to identify small balls about
is defined using the local orientations to identify small balls about  and
and  . The diffeomorphism type of
. The diffeomorphism type of 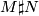 is well-defined: in fact
is well-defined: in fact 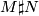 is the outcome of 0-surgery on
is the outcome of 0-surgery on 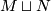 . The essential point is [Hirsch] which states, for any
. The essential point is [Hirsch] which states, for any  and any two compatibly oriented embeddings
and any two compatibly oriented embeddings 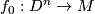 and
and 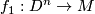 , that
, that  is isotopic to
is isotopic to  .
.
If  and
and  are oriented manifolds the connected sum
are oriented manifolds the connected sum 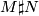 is a well-defined up to diffeomorphism. Note that orientation matters! The canoical example is
is a well-defined up to diffeomorphism. Note that orientation matters! The canoical example is
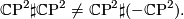
The manifolds are not even homotopy equivalent: the first has signature 2 the other signature 0. The following elementary lemma is often useful to remember.
Lemma 1.1.
Let  and
and  be locally oriented manifolds such that there is a diffeomoprhism
be locally oriented manifolds such that there is a diffeomoprhism 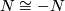 , then
, then 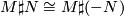 .
.
2 References