Connected sum
m (→Connected sum of smooth manifolds) |
|||
| (9 intermediate revisions by 2 users not shown) | |||
| Line 2: | Line 2: | ||
== Connected sum of smooth manifolds == | == Connected sum of smooth manifolds == | ||
<wikitex>; | <wikitex>; | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Let $M_0$ and $M_1$ be oriented closed smooth connected $n$-manifolds. Their connected sum is an oriented closed smooth connected $n$-manifold | Let $M_0$ and $M_1$ be oriented closed smooth connected $n$-manifolds. Their connected sum is an oriented closed smooth connected $n$-manifold | ||
| − | + | $$ M_1 \sharp M_2 $$ | |
| − | which is defined as follows (c.f. \cite{Kervaire&Milnor1963|Section 2}. Choose smooth embeddings | + | which is defined as follows (c.f. \cite{Kervaire&Milnor1963|Section 2}). Choose smooth embeddings |
| − | + | $$ i_0 \colon D^n \to M_0 \quad \text{and} \quad i_1 \colon D^n \to M_1 $$ | |
where $i_1$ preserves orientations and $i_2$ reverses orientations. The connected sum is formed from the | where $i_1$ preserves orientations and $i_2$ reverses orientations. The connected sum is formed from the | ||
disjoint union | disjoint union | ||
| − | \ | + | $$ \bigl( M_0 - i_0(0) \bigr) \sqcup \bigl(M_1 - i_1(0) \bigr) $$ |
by identifying $i_0(tu)$ with $i_1((1-t)u)$ for $u \in S^{n-1}$ and $0 < t < 1$. The smooth structure on | by identifying $i_0(tu)$ with $i_1((1-t)u)$ for $u \in S^{n-1}$ and $0 < t < 1$. The smooth structure on | ||
$M_0 \sharp M_1$ is obtain from the charts on $M_0 - i_0(0)$ and $M_1 - i_1(0)$. The orientation on | $M_0 \sharp M_1$ is obtain from the charts on $M_0 - i_0(0)$ and $M_1 - i_1(0)$. The orientation on | ||
$M_0 \sharp M_1$ is chosen to be the one compatible with the orientation of $M_0$ and $M_1$. | $M_0 \sharp M_1$ is chosen to be the one compatible with the orientation of $M_0$ and $M_1$. | ||
| − | A fundamental lemma of differential topology, \cite{Palais1959|Theorem 5.5} \cite{Cerf1961} states that any | + | A fundamental lemma of differential topology, \cite{Palais1959|Theorem 5.5} and \cite{Cerf1961} states that any |
| − | two orientation preserving | + | two orientation preserving smooth embeddings of the $n$-disc into a closed oriented smooth $n$-manifold are isotopic. As a consequence we have the following lemma. |
| − | {{beginthm|Lemma|\cite{Kervaire&Milnor1963|Lemma 2.1}}} | + | {{beginthm|Lemma|\cite{Kervaire&Milnor1963|Lemma 2.1} }} |
The connected sum operation is well defined, associative and commutative up to | The connected sum operation is well defined, associative and commutative up to | ||
orientation preserving diffeomoprhism. The sphere $S^n$ serves as the identity element. | orientation preserving diffeomoprhism. The sphere $S^n$ serves as the identity element. | ||
| Line 29: | Line 24: | ||
of oriented manifolds. | of oriented manifolds. | ||
| − | {{beginthm|Lemma|c.f. \cite{Kervaire&Milnor1963|Lemma 2.2 | + | {{beginthm|Lemma|c.f. \cite{Kervaire&Milnor1963|Lemma 2.2} }} |
Let $M_0$, $M_0'$ and $M_1$ be oriented closed connected smooth manifold. Suppose that $M_0$ is [[h-cobordism|h-cobordant]] to $M_0'$, resp. bordant to $M_0'$ then $M_0 \sharp M_1$ is h-cobordant, resp. bordant, to $M_0' \sharp M_1$. | Let $M_0$, $M_0'$ and $M_1$ be oriented closed connected smooth manifold. Suppose that $M_0$ is [[h-cobordism|h-cobordant]] to $M_0'$, resp. bordant to $M_0'$ then $M_0 \sharp M_1$ is h-cobordant, resp. bordant, to $M_0' \sharp M_1$. | ||
{{endthm}} | {{endthm}} | ||
| + | </wikitex> | ||
<!-- If $M$ and $N$ are oriented manifolds the connected sum $M \sharp N$ is a well-defined up to diffeomorphism. Note that orientation matters! --> | <!-- If $M$ and $N$ are oriented manifolds the connected sum $M \sharp N$ is a well-defined up to diffeomorphism. Note that orientation matters! --> | ||
| − | == | + | <!-- Let $M$ be a compact connected n-manifold with base point $m \in \mathrm{int} M$. Recall that that a local orientation for $M$ is a choice of orientation of $TM_m$, the tangent space to $M$ at $m$. We write $-M$ for $M$ with the opposition orientation at $m$. Of course, if $M$ is orientable then a local orientation for $M$ defines an orientation on $M$. |
| + | If $M$ and $N$ are locally oriented n-manifolds then their [[Wikipedia:Connected_sum|connected sum]] is defined by | ||
| + | $$ M \sharp N = ((M - m) \cup (N - n))/ \simeq$$ | ||
| + | where $\simeq$ is defined using the local orientations to identify small balls about $m$ and $n$. The diffeomorphism type of $M \sharp N$ is well-defined: in fact $M \sharp N$ is the outcome of 0-surgery on $M \sqcup N$. The essential point is \cite{Hirsch} which states, for any $M$ and any two compatibly oriented embeddings $f_1: D^n \to M$ and $f_1 : D^n \to M$, that $f_0$ is isotopic to $f_1$. --> | ||
| + | |||
| + | == Connected sum of topological manifolds == | ||
| + | <wikitex>; | ||
| + | Connected sum is a well-defined operation up to orientation preserving homeomorphism for oriented closed connected topological $n$-manifolds. However, there is no analogue of the Palais/Cerf result and so the proof is more complicated. See the mathoverflow discussion cited [[#External links|below]]. | ||
| + | </wikitex> | ||
| + | |||
| + | == Examples== | ||
| + | <wikitex>; | ||
The orientation of the manifolds is important in general. The canonical example is | The orientation of the manifolds is important in general. The canonical example is | ||
$$ \CP^2 \sharp \CP^2 \neq \CP^2 \sharp (-\CP^2).$$ | $$ \CP^2 \sharp \CP^2 \neq \CP^2 \sharp (-\CP^2).$$ | ||
| Line 45: | Line 52: | ||
There are diffeomorphisms | There are diffeomorphisms | ||
# $M \sharp M \cong M \sharp (S^3 \times S^4)$ | # $M \sharp M \cong M \sharp (S^3 \times S^4)$ | ||
| − | # $M \sharp \Sigma \cong M$ for any homotopy sphere $\Sigma$. (Recall that the | + | # $M \sharp \Sigma \cong M$ for any homotopy sphere $\Sigma$. (Recall that the group of [[Exotic spheres|homotopy 7-spheres]], $\Theta_7$ is isomorphic to $\Z/28$.) |
| − | group of [[Exotic spheres|homotopy 7-spheres]], $\Theta_7$ is isomorphic to $\Z/28$.) | + | |
{{endthm}} | {{endthm}} | ||
{{beginproof}} | {{beginproof}} | ||
| Line 55: | Line 61: | ||
2.) This is a special case of \cite{Wilkens1974/75|Theorem 1}. | 2.) This is a special case of \cite{Wilkens1974/75|Theorem 1}. | ||
{{endproof}} | {{endproof}} | ||
| + | </wikitex> | ||
== Properties == | == Properties == | ||
| + | <wikitex>; | ||
Let $M$ be a closed connected $n$-manifold and let | Let $M$ be a closed connected $n$-manifold and let | ||
| − | $$M^\bullet : = M \setminus | + | $$M^\bullet : = M \setminus \textup{Int}(D^n)$$ |
denote the compact manifold obtained from $M$ by deleting a small embedded open $n$-disc. From the definition | denote the compact manifold obtained from $M$ by deleting a small embedded open $n$-disc. From the definition | ||
it is clear that | it is clear that | ||
| Line 69: | Line 77: | ||
$$ \pi_1(M_0 \sharp M_1) \cong \pi_1(M_0) \ast \pi_1(M_2) .$$ | $$ \pi_1(M_0 \sharp M_1) \cong \pi_1(M_0) \ast \pi_1(M_2) .$$ | ||
{{endthm}} | {{endthm}} | ||
| − | |||
</wikitex> | </wikitex> | ||
| − | |||
== References == | == References == | ||
{{#RefList:}} | {{#RefList:}} | ||
| − | |||
== External links == | == External links == | ||
* [http://mathoverflow.net/questions/121571/connected-sum-of-topological-manifolds Mathoverflow:Connected sum of topological manifolds] | * [http://mathoverflow.net/questions/121571/connected-sum-of-topological-manifolds Mathoverflow:Connected sum of topological manifolds] | ||
| − | + | * The Encyclopedia of Mathematics article on [http://www.encyclopediaofmath.org/index.php/Connected_sum connected sum] | |
| − | [[ | + | * The Wikipedia page about [[Wikipedia:Connected_sum|connected sum]] |
[[Category:Definitions]] | [[Category:Definitions]] | ||
Latest revision as of 15:13, 6 June 2014
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Connected sum of smooth manifolds
Let 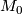 and
and  be oriented closed smooth connected
be oriented closed smooth connected  -manifolds. Their connected sum is an oriented closed smooth connected
-manifolds. Their connected sum is an oriented closed smooth connected  -manifold
-manifold
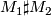
which is defined as follows (c.f. [Kervaire&Milnor1963, Section 2]). Choose smooth embeddings
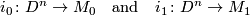
where 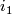 preserves orientations and
preserves orientations and 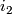 reverses orientations. The connected sum is formed from the
disjoint union
reverses orientations. The connected sum is formed from the
disjoint union
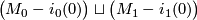
by identifying 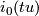 with
with 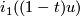 for
for 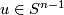 and
and 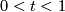 . The smooth structure on
. The smooth structure on
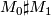 is obtain from the charts on
is obtain from the charts on 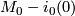 and
and 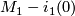 . The orientation on
. The orientation on
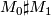 is chosen to be the one compatible with the orientation of
is chosen to be the one compatible with the orientation of 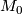 and
and  .
.
A fundamental lemma of differential topology, [Palais1959, Theorem 5.5] and [Cerf1961] states that any
two orientation preserving smooth embeddings of the  -disc into a closed oriented smooth
-disc into a closed oriented smooth  -manifold are isotopic. As a consequence we have the following lemma.
-manifold are isotopic. As a consequence we have the following lemma.
Lemma 1.1 [Kervaire&Milnor1963, Lemma 2.1] .
The connected sum operation is well defined, associative and commutative up to
orientation preserving diffeomoprhism. The sphere  serves as the identity element.
serves as the identity element.
The connected sum operation also descends to give well-defined operations on larger equivalence classes of oriented manifolds.
Lemma 1.2 c.f. [Kervaire&Milnor1963, Lemma 2.2] .
Let 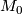 ,
, 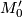 and
and  be oriented closed connected smooth manifold. Suppose that
be oriented closed connected smooth manifold. Suppose that 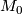 is h-cobordant to
is h-cobordant to 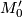 , resp. bordant to
, resp. bordant to 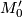 then
then 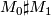 is h-cobordant, resp. bordant, to
is h-cobordant, resp. bordant, to 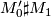 .
.
[edit] 2 Connected sum of topological manifolds
Connected sum is a well-defined operation up to orientation preserving homeomorphism for oriented closed connected topological  -manifolds. However, there is no analogue of the Palais/Cerf result and so the proof is more complicated. See the mathoverflow discussion cited below.
-manifolds. However, there is no analogue of the Palais/Cerf result and so the proof is more complicated. See the mathoverflow discussion cited below.
[edit] 3 Examples
The orientation of the manifolds is important in general. The canonical example is
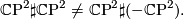
The manifolds are not even homotopy equivalent: the first has signature 2 the other signature 0. The following elementary lemma is often useful to remember.
Lemma 3.1.
Let  and
and  be locally oriented manifolds such that there is a diffeomoprhism
be locally oriented manifolds such that there is a diffeomoprhism 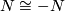 , then
, then 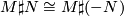 .
.
Connected sum decompositions of manifolds are far from being unique. For example, let 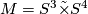 be the total space of the non-trivial 3-sphere bundle over
be the total space of the non-trivial 3-sphere bundle over 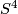 with Euler class zero and Pontrjagin class four times a preferred generator of
with Euler class zero and Pontrjagin class four times a preferred generator of 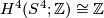 .
.
Lemma 3.2 c.f.[Wilkens1974/75, Theorem 1] . There are diffeomorphisms
-
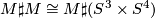
-
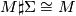 for any homotopy sphere
for any homotopy sphere  . (Recall that the group of homotopy 7-spheres,
. (Recall that the group of homotopy 7-spheres, 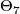 is isomorphic to
is isomorphic to 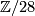 .)
.)
Proof.
1.) The manifold  is the boundary of the total space of the corresponding disc bundle
is the boundary of the total space of the corresponding disc bundle 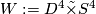 and hence
and hence 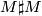 is the boundary of
is the boundary of 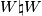 . Compact
. Compact  -connected
-connected  -manifolds were classified
in [Wall1962a, Section 2]. Since the intersection form of
-manifolds were classified
in [Wall1962a, Section 2]. Since the intersection form of 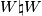 is trivial, it is a simple consequence
of Wall's classification that there is a diffeomorphism
is trivial, it is a simple consequence
of Wall's classification that there is a diffeomorphism 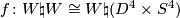 . Restricting
. Restricting  to the boundary gives the desired diffeomorphism.
to the boundary gives the desired diffeomorphism.
2.) This is a special case of [Wilkens1974/75, Theorem 1].

[edit] 4 Properties
Let  be a closed connected
be a closed connected  -manifold and let
-manifold and let
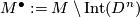
denote the compact manifold obtained from  by deleting a small embedded open
by deleting a small embedded open  -disc. From the definition
it is clear that
-disc. From the definition
it is clear that
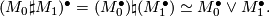
Here 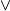 denotes the one point union of topological spaces and
denotes the one point union of topological spaces and 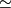 indicates that two spaces are
homotopy equivalent. Applying Van Kampen's Theorem we immediately obtain the following lemma.
indicates that two spaces are
homotopy equivalent. Applying Van Kampen's Theorem we immediately obtain the following lemma.
Lemma 4.1.
Let the dimension  be three or greater. Then the fundamental group of a connected sum is the free
product of the fundamental group of the components:
be three or greater. Then the fundamental group of a connected sum is the free
product of the fundamental group of the components:
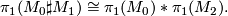
[edit] 5 References
- [Cerf1961] J. Cerf, Topologie de certains espaces de plongements, Bull. Soc. Math. France 89 (1961), 227–380. MR0140120 (25 #3543) Zbl 0101.16001
- [Kervaire&Milnor1963] M. A. Kervaire and J. W. Milnor, Groups of homotopy spheres. I, Ann. of Math. (2) 77 (1963), 504–537. MR0148075 (26 #5584) Zbl 0115.40505
- [Palais1959] R. S. Palais, Natural operations on differential forms, Trans. Amer. Math. Soc. 92 (1959), 125–141. MR0116352 (22 #7140) Zbl 0092.30802
- [Wall1962a] C. T. C. Wall, Classification of
 -connected
-connected  -manifolds, Ann. of Math. (2) 75 (1962), 163–189. MR0145540 (26 #3071) Zbl 0218.57022
-manifolds, Ann. of Math. (2) 75 (1962), 163–189. MR0145540 (26 #3071) Zbl 0218.57022
- [Wilkens1974/75] D. L. Wilkens, On the inertia groups of certain manifolds, J. London Math. Soc. (2) 9 (1974/75), 537–548. MR0383435 (52 #4316)
[edit] 6 External links
- Mathoverflow:Connected sum of topological manifolds
- The Encyclopedia of Mathematics article on connected sum
- The Wikipedia page about connected sum
 be oriented closed smooth connected
be oriented closed smooth connected  -manifolds. Their connected sum is an oriented closed smooth connected
-manifolds. Their connected sum is an oriented closed smooth connected  -manifold
-manifold
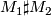
which is defined as follows (c.f. [Kervaire&Milnor1963, Section 2]). Choose smooth embeddings
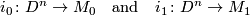
where 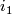 preserves orientations and
preserves orientations and 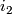 reverses orientations. The connected sum is formed from the
disjoint union
reverses orientations. The connected sum is formed from the
disjoint union
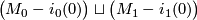
by identifying 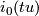 with
with 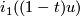 for
for 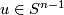 and
and 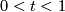 . The smooth structure on
. The smooth structure on
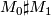 is obtain from the charts on
is obtain from the charts on 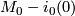 and
and 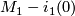 . The orientation on
. The orientation on
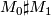 is chosen to be the one compatible with the orientation of
is chosen to be the one compatible with the orientation of 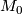 and
and  .
.
A fundamental lemma of differential topology, [Palais1959, Theorem 5.5] and [Cerf1961] states that any
two orientation preserving smooth embeddings of the  -disc into a closed oriented smooth
-disc into a closed oriented smooth  -manifold are isotopic. As a consequence we have the following lemma.
-manifold are isotopic. As a consequence we have the following lemma.
Lemma 1.1 [Kervaire&Milnor1963, Lemma 2.1] .
The connected sum operation is well defined, associative and commutative up to
orientation preserving diffeomoprhism. The sphere  serves as the identity element.
serves as the identity element.
The connected sum operation also descends to give well-defined operations on larger equivalence classes of oriented manifolds.
Lemma 1.2 c.f. [Kervaire&Milnor1963, Lemma 2.2] .
Let 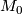 ,
, 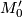 and
and  be oriented closed connected smooth manifold. Suppose that
be oriented closed connected smooth manifold. Suppose that 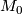 is h-cobordant to
is h-cobordant to 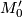 , resp. bordant to
, resp. bordant to 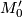 then
then 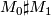 is h-cobordant, resp. bordant, to
is h-cobordant, resp. bordant, to 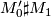 .
.
[edit] 2 Connected sum of topological manifolds
Connected sum is a well-defined operation up to orientation preserving homeomorphism for oriented closed connected topological  -manifolds. However, there is no analogue of the Palais/Cerf result and so the proof is more complicated. See the mathoverflow discussion cited below.
-manifolds. However, there is no analogue of the Palais/Cerf result and so the proof is more complicated. See the mathoverflow discussion cited below.
[edit] 3 Examples
The orientation of the manifolds is important in general. The canonical example is
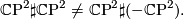
The manifolds are not even homotopy equivalent: the first has signature 2 the other signature 0. The following elementary lemma is often useful to remember.
Lemma 3.1.
Let  and
and  be locally oriented manifolds such that there is a diffeomoprhism
be locally oriented manifolds such that there is a diffeomoprhism 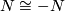 , then
, then 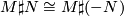 .
.
Connected sum decompositions of manifolds are far from being unique. For example, let 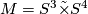 be the total space of the non-trivial 3-sphere bundle over
be the total space of the non-trivial 3-sphere bundle over 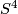 with Euler class zero and Pontrjagin class four times a preferred generator of
with Euler class zero and Pontrjagin class four times a preferred generator of 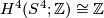 .
.
Lemma 3.2 c.f.[Wilkens1974/75, Theorem 1] . There are diffeomorphisms
-
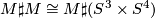
-
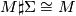 for any homotopy sphere
for any homotopy sphere  . (Recall that the group of homotopy 7-spheres,
. (Recall that the group of homotopy 7-spheres, 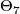 is isomorphic to
is isomorphic to 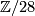 .)
.)
Proof.
1.) The manifold  is the boundary of the total space of the corresponding disc bundle
is the boundary of the total space of the corresponding disc bundle 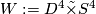 and hence
and hence 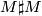 is the boundary of
is the boundary of 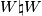 . Compact
. Compact  -connected
-connected  -manifolds were classified
in [Wall1962a, Section 2]. Since the intersection form of
-manifolds were classified
in [Wall1962a, Section 2]. Since the intersection form of 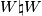 is trivial, it is a simple consequence
of Wall's classification that there is a diffeomorphism
is trivial, it is a simple consequence
of Wall's classification that there is a diffeomorphism 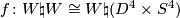 . Restricting
. Restricting  to the boundary gives the desired diffeomorphism.
to the boundary gives the desired diffeomorphism.
2.) This is a special case of [Wilkens1974/75, Theorem 1].

[edit] 4 Properties
Let  be a closed connected
be a closed connected  -manifold and let
-manifold and let
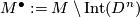
denote the compact manifold obtained from  by deleting a small embedded open
by deleting a small embedded open  -disc. From the definition
it is clear that
-disc. From the definition
it is clear that
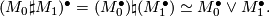
Here 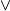 denotes the one point union of topological spaces and
denotes the one point union of topological spaces and 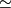 indicates that two spaces are
homotopy equivalent. Applying Van Kampen's Theorem we immediately obtain the following lemma.
indicates that two spaces are
homotopy equivalent. Applying Van Kampen's Theorem we immediately obtain the following lemma.
Lemma 4.1.
Let the dimension  be three or greater. Then the fundamental group of a connected sum is the free
product of the fundamental group of the components:
be three or greater. Then the fundamental group of a connected sum is the free
product of the fundamental group of the components:
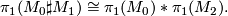
[edit] 5 References
- [Cerf1961] J. Cerf, Topologie de certains espaces de plongements, Bull. Soc. Math. France 89 (1961), 227–380. MR0140120 (25 #3543) Zbl 0101.16001
- [Kervaire&Milnor1963] M. A. Kervaire and J. W. Milnor, Groups of homotopy spheres. I, Ann. of Math. (2) 77 (1963), 504–537. MR0148075 (26 #5584) Zbl 0115.40505
- [Palais1959] R. S. Palais, Natural operations on differential forms, Trans. Amer. Math. Soc. 92 (1959), 125–141. MR0116352 (22 #7140) Zbl 0092.30802
- [Wall1962a] C. T. C. Wall, Classification of
 -connected
-connected  -manifolds, Ann. of Math. (2) 75 (1962), 163–189. MR0145540 (26 #3071) Zbl 0218.57022
-manifolds, Ann. of Math. (2) 75 (1962), 163–189. MR0145540 (26 #3071) Zbl 0218.57022
- [Wilkens1974/75] D. L. Wilkens, On the inertia groups of certain manifolds, J. London Math. Soc. (2) 9 (1974/75), 537–548. MR0383435 (52 #4316)
[edit] 6 External links
- Mathoverflow:Connected sum of topological manifolds
- The Encyclopedia of Mathematics article on connected sum
- The Wikipedia page about connected sum