Concordance implies isotopy for smooth structures on 3-manifolds?
1 Problem
A  -manifold has a smooth structure which is essentially unique. One question is what does ``essentially unique" mean.
-manifold has a smooth structure which is essentially unique. One question is what does ``essentially unique" mean.
In high dimensions you can classify smooth structures either up to concordance or up to isotopy. In high dimensions concordance implies isotopy.
If you have a topological manifold 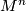 and a smooth manifold
and a smooth manifold 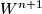 homeomorphic to
homeomorphic to 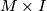 , you can ask if that smooth manifold
, you can ask if that smooth manifold  is diffeomorphic to a product,
is diffeomorphic to a product,
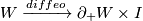
This ``concordance implies isotopy" theorem of Kirby-Siebenmann and Hirsch is:
\begin{itemize}
\item true in high dimensions,  .
.
If you have a topological manifold 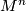 , you can classify smooth structures as homotopy classes of maps
, you can classify smooth structures as homotopy classes of maps
![\displaystyle \mathcal{S}^{TOP/O}(M^n) = [M^n, TOP/O]](/images/math/5/2/3/523c667c682f66d0b0022e4422f79140.png)
The structure set 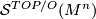 is the set of classes of smoothings on
is the set of classes of smoothings on 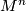 . But it is important to decide what is meant by the ``structure" and there are two possible equivalence relations: concordance or isotopy.
. But it is important to decide what is meant by the ``structure" and there are two possible equivalence relations: concordance or isotopy.
A smoothing is a homeomorphism from a smooth manifold  to
to 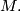

Two smoothings  and
and  are \textit{concordant} if there is a smooth manifold
are \textit{concordant} if there is a smooth manifold 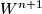 and a homeomorphism to
and a homeomorphism to 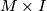 that restricts to these two smoothings.
that restricts to these two smoothings.
\medskip
Two smoothings  and
and  are isotopic if there is a smooth manifold
are isotopic if there is a smooth manifold  and a level-preserving homeomorphism
and a level-preserving homeomorphism 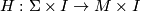 ,
,
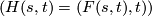
inducing 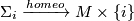 for
for 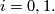
Theorem 1.1. If dim 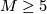 , then concordant structures are isotopic (and hence diffeomorphic).
, then concordant structures are isotopic (and hence diffeomorphic).
\item false for simply-connected  -manifolds by the failure of the
-manifolds by the failure of the  -cobordism theorem. Cappell and Shanneson proved in the non-simply connected case that there are counterexamples to the
-cobordism theorem. Cappell and Shanneson proved in the non-simply connected case that there are counterexamples to the  -cobordism theorem.
\item we don't know the answer for
-cobordism theorem.
\item we don't know the answer for  .
\end{itemize}
.
\end{itemize}
aa