Complex bordism

Revision as of 16:07, 10 March 2010

1 Introduction

A unitary struture ${{Authors|Taras Panov}} {{Redirect|Unitary bordism|B|A}} == Introduction == <wikitex>; A unitary struture $\bar \nu$ on a manifold $M$ is a choice of weak complex structure on the stable normal bundle of $M$. By the [[B-Bordism#Pontrjagin-Thom isomorphism|Pontrjagin-Thom isomorphism]] the bordism groups of closed unitary manifolds $(M, \bar \nu)$ are isomorphic to the homotopy groups of the Thom spectrum $MU$, $\Omega_*^{U} \cong \pi_n(MU)$. This page is presently under construction. For more information see \cite{Stong1968}. </wikitex> == References == {{#RefList:}} <!-- Please modify these headings or choose other headings according to your needs. 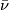--> [[Category:Manifolds]] {{Stub}}\bar \nu$ on a manifold $M$ is a choice of weak complex structure on the stable normal bundle of $M$. 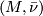By the Pontrjagin-Thom isomorphism the bordism groups of closed unitary manifolds $(M, \bar \nu)$ are isomorphic to the homotopy groups of the Thom spectrum $MU$, $\Omega_*^{U} \cong \pi_n(MU)$.

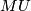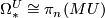This page is presently under construction. For more information see [Stong1968].

2 Stably complex structures

3 Definition of bordism and cobordism

4 Geometric cobordisms

5 Structure results

6 Multiplicative generators

== Formal group laws and genera

== Adams-Novikov spectral sequence

7 References

• [Stong1968] R. E. Stong, Notes on cobordism theory, Princeton University Press, Princeton, N.J., 1968. MR0248858 (40 #2108) Zbl 0277.57010