Algebraic surgery X (Ex)
From Manifold Atlas
(Difference between revisions)
Tibor Macko (Talk | contribs) (Created page with "<wikitex>; Let $(f,b) \colon M \rightarrow X$ be a degree one normal map of $n$-GPC. Denote by $\nu_M$, $\nu_X$ the respective SNFs. We form the $(n+1)$-dimensional geometric ...") |
Markullmann (Talk | contribs) m (correct Poincaré's name) |
||
| Line 2: | Line 2: | ||
Let $(f,b) \colon M \rightarrow X$ be a degree one normal map of $n$-GPC. | Let $(f,b) \colon M \rightarrow X$ be a degree one normal map of $n$-GPC. | ||
Denote by $\nu_M$, $\nu_X$ the respective SNFs. We form the | Denote by $\nu_M$, $\nu_X$ the respective SNFs. We form the | ||
| − | $(n+1)$-dimensional geometric (normal, | + | $(n+1)$-dimensional geometric (normal, Poincaré) pair |
$$ | $$ | ||
\big( (W,M \sqcup X), (\nu_W,\nu_{M \sqcup X}), (\rho_W,\rho_{M | \big( (W,M \sqcup X), (\nu_W,\nu_{M \sqcup X}), (\rho_W,\rho_{M | ||
Latest revision as of 14:16, 1 June 2012
Let 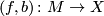 be a degree one normal map of
be a degree one normal map of 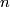 -GPC.
Denote by
-GPC.
Denote by 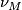 ,
, 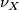 the respective SNFs. We form the
the respective SNFs. We form the
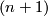 -dimensional geometric (normal, Poincaré) pair
-dimensional geometric (normal, Poincaré) pair
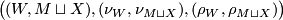
with  . The symbol
. The symbol  denotes the
denotes the 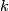 -spherical
fibration over
-spherical
fibration over 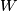 induced by
induced by  and
and
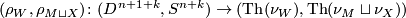
is the map induced by 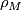 and
and 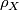 and denote
and denote 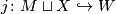 .
.
Let 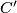 be the underlying chain complex obtained by algebraic surgery on the
be the underlying chain complex obtained by algebraic surgery on the
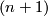 -dimensional symmetric pair
-dimensional symmetric pair
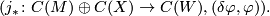
Show that it is homotopy equivalent to the mapping cone 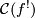 of the 'Umkehr' map associated to
of the 'Umkehr' map associated to 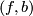 .
.