6-manifolds: 1-connected
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Let 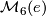 be the set of diffeomorphism classes of closed oriented smooth simply-connected 6-manifolds
be the set of diffeomorphism classes of closed oriented smooth simply-connected 6-manifolds  .
.
Similarly, let 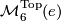 be the set of homeomorphism classes of closed, oriented topological manifolds.
be the set of homeomorphism classes of closed, oriented topological manifolds.
In this article we report on the calculation of 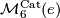 and
and 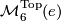 begun by [Smale1962], extended in [Wall1966] in [Jupp1973] and completed in [Zhubr2000]. We shall write
begun by [Smale1962], extended in [Wall1966] in [Jupp1973] and completed in [Zhubr2000]. We shall write 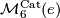 for either
for either 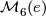 or
or 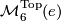 . An excellent summary for the case where
. An excellent summary for the case where 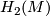 is torsion free may be found in [Okonek&Van de Ven1995].
is torsion free may be found in [Okonek&Van de Ven1995].
2 Examples and constructions
We first present some familiar 6-manifolds.
-
Tex syntax error
, the standard 6-sphere. -
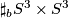 , the
, the Tex syntax error
-fold connected sum ofTex syntax error
. -
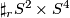 , the
, the  -fold connected sum of
-fold connected sum of 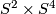 .
.
-
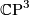 , 3-dimensional complex projective space.
, 3-dimensional complex projective space.
-
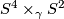 , the non-trivial linear 4-sphere bundle over
, the non-trivial linear 4-sphere bundle over  .
.
- For each
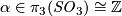 we have
we have 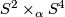 , the corresponding 2-sphere bundle over
, the corresponding 2-sphere bundle over  . If we write 1 for a generator of
. If we write 1 for a generator of 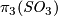 then
then 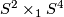 is diffeomorphic to
is diffeomorphic to 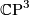 .
.
Surgery on framed links. Let 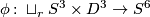 be a framed link. Then
be a framed link. Then 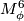 , the outcome of surgery on
, the outcome of surgery on  , is a simply connected Spinable 6-manifold with
, is a simply connected Spinable 6-manifold with 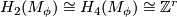 and
and 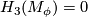 .
.
- ??? Complete intersections of some form.
3 Invariants
The second Stiefel-Whitney class of  is an element of
is an element of 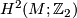 which we regard as a homomorphism
which we regard as a homomorphism 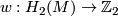 .
.
- The first Pontrjagin class
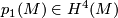 .
.
- The Kirby-Siebenmann class
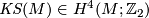
- The cup product
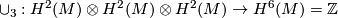 .
.
These invariants satisfy the following relation
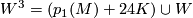
for all 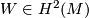 which reduce to
which reduce to 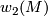 mod
mod  and for all
and for all 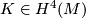 which reduce to
which reduce to 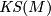 mod
mod  . As [Okonek&Van de Ven1995, p. 300] remark, in the smooth case this follows from the integrality of the
. As [Okonek&Van de Ven1995, p. 300] remark, in the smooth case this follows from the integrality of the 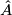 -genus but in the topological case requires further arguments carried out in [Jupp1973].
-genus but in the topological case requires further arguments carried out in [Jupp1973].
4 Classification
4.1 Preliminaries
Let 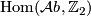 be the set of isomorphism classes of pairs
be the set of isomorphism classes of pairs 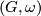 where
where  is a finitely generated abelian group
is a finitely generated abelian group 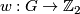 is a homomorphism and where an isomorphism is an isomorphism of groups commuting with the homomorphisms to
is a homomorphism and where an isomorphism is an isomorphism of groups commuting with the homomorphisms to  . The second Stiefel-Whitney classes defines a surjection
. The second Stiefel-Whitney classes defines a surjection
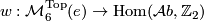
and we let ![\mathcal{M}^{\Cat}_6(G, w) = w^{-1}([G, w])](/images/math/8/0/c/80c4ca5b3295d1266199cb14719c7754.png) denote the set of isomorphism classes of 6-manifolds with prescribed second Stiefel-Whitney class. We obtain the decomposition
denote the set of isomorphism classes of 6-manifolds with prescribed second Stiefel-Whitney class. We obtain the decomposition
![\displaystyle \mathcal{M}^{\Cat}_{6}(e) = \cup_{[G, w]} \mathcal{M}^{\Cat}_{6}(G, w)](/images/math/b/c/4/bc42f0b862f212b051befba26a41415e.png)
where ![[G, w]](/images/math/9/e/1/9e1553e9793f5bee0f5d92936aa7c277.png) ranges over all of
ranges over all of 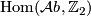 .
.
4.2 The splitting Theorem
Theorem 3 4.1 (Wall).
Let  be a closed, smooth, simply-connected 6-manifold with
be a closed, smooth, simply-connected 6-manifold with 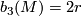 . Then up to diffeomorphism, there is a unique maniofld
. Then up to diffeomorphism, there is a unique maniofld  with
with 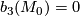 such that
such that  is diffeomorphic to
is diffeomorphic to 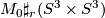 .
.
4.3 Smoothing theory
Theorem 1 4.2.
Let  be a simply-connected, topological 6-manifold. The Kirby-Siebenmann class,
be a simply-connected, topological 6-manifold. The Kirby-Siebenmann class, 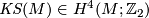 is the sole obstruction to
is the sole obstruction to  admitting a smooth structure.
admitting a smooth structure.
Theorem 2 4.3.
Every homeomorphism 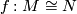 of simply-connected, smooth
of simply-connected, smooth  -manifolds is topologically isotopic to a diffeomorphism. Hence we have an injection
-manifolds is topologically isotopic to a diffeomorphism. Hence we have an injection
Tex syntax error
5 6-manifolds with torsion free second homology
...
6 Further discussion
...
7 References
- [Jupp1973] P. E. Jupp, Classification of certain
 -manifolds, Proc. Cambridge Philos. Soc. 73 (1973), 293–300. MR0314074 (47 #2626) Zbl 0249.57005
-manifolds, Proc. Cambridge Philos. Soc. 73 (1973), 293–300. MR0314074 (47 #2626) Zbl 0249.57005
- [Okonek&Van de Ven1995] C. Okonek and A. Van de Ven, Cubic forms and complex
 -folds, Enseign. Math. (2) 41 (1995), no.3-4, 297–333. MR1365849 (97b:32035) Zbl 0869.14018
-folds, Enseign. Math. (2) 41 (1995), no.3-4, 297–333. MR1365849 (97b:32035) Zbl 0869.14018
- [Smale1962] S. Smale, On the structure of
 -manifolds, Ann. of Math. (2) 75 (1962), 38–46. MR0141133 (25 #4544) Zbl 0101.16103
-manifolds, Ann. of Math. (2) 75 (1962), 38–46. MR0141133 (25 #4544) Zbl 0101.16103
- [Wall1966] C. T. C. Wall, Classification problems in differential topology. V. On certain
 -manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601
-manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601
- [Zhubr2000] A. V. Zhubr, Closed simply connected six-dimensional manifolds: proofs of classification theorems, Algebra i Analiz 12 (2000), no.4, 126–230. MR1793619 (2001j:57041)