6-manifolds: 1-connected
m (moved Simply-connected 6-manifolds to 6-manifolds: 1-connected: To start names with dimension) |
|||
| Line 20: | Line 20: | ||
* ??? Complete intersections of some form. | * ??? Complete intersections of some form. | ||
<wikitex>; | <wikitex>; | ||
| + | |||
| + | == Invariants == | ||
| + | The second [[wikipedia:Stiefel–Whitney_class|Stiefel-Whitney class]] of $M$ is an element of $H^2(M; \Zz_2)$ which we regard as a homomorphism $w\co H_2(M) \rightarrow \Zz_2$. | ||
| + | |||
| + | * The first [[wikipedia:Pontrjagin_class|Pontrjagin class]] $p_1(M) \in H^4(M)$. | ||
| + | * The Kirby-Siebenmann class $\KS(M) \in H^4(M; \Zz_2)$ | ||
| + | * The cup product $\cup_3\co H^2(M) \otimes H^2(M) \otimes H^2(M) \rightarrow H^6(M) = \Zz$. | ||
| + | These invariants satisfy the following relation | ||
| + | $$W^3 = (p_1(M) + 24K) \cup W$$ | ||
| + | for all $W \in H^2(M)$ which reduce to $w_2(M)$ mod $2$ and for all $K \in H^4(M)$ which reduce to $\KS(M)$ mod $2$. | ||
== Classification == | == Classification == | ||
| + | |||
| + | === Preliminaries === | ||
| + | <wikitex>; | ||
| + | Let $\Hom({\mathcal Ab}, \Zz_2)$ be the set of isomorphism classes of pairs $(G, \omega)$ where $G$ is a finitely generated abelian group $w\co G \rightarrow \Zz_2$ is a homomorphism and where an isomorphism is an isomorphism of groups commuting with the homomorphisms to $\Zz_2$. The second Stiefel-Whitney classes defines a surjection | ||
| + | $$ w\co\mathcal{M}_{6}^{\Top}(e) \rightarrow \Hom({\mathcal Ab}, \Zz_2)$$ | ||
| + | and we let $\mathcal{M}^{\Cat}_6(G, w) = w^{-1}([G, w])$ denote the set of isomorphism classes of 6-manifolds with prescribed second Stiefel-Whitney class. We obtain the decomposition | ||
| + | $$ \mathcal{M}^{\Cat}_{6}(e) = \cup_{[G, w]} \mathcal{M}^{\Cat}_{6}(G, w)$$ | ||
| + | where $[G, w]$ ranges over all of $\Hom({\mathcal Ab}, \Zz_2)$. | ||
| + | </wikitex> | ||
| + | |||
| + | === The splitting Theorem === | ||
| + | <wikitex>; | ||
| + | {{beginthm|Theorem 3|(Wall)}} | ||
| + | Let $M$ be a closed, smooth, simply-connected 6-manifold with $b_3(M) = 2r$. Then up to diffeomorphism, there is a unique maniofld $M_0$ with $b_3(M_0) = 0$ such that $M$ is diffeomorphic to $M_0 \sharp_r(S^3 \times S^3)$. | ||
| + | {{endthm}} | ||
| + | </wikitex> | ||
| + | |||
=== Smoothing theory === | === Smoothing theory === | ||
<wikitex>; | <wikitex>; | ||
| Line 34: | Line 61: | ||
</wikitex> | </wikitex> | ||
| − | == | + | == 6-manifolds with torsion free second homology == |
<wikitex>; | <wikitex>; | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
</wikitex> | </wikitex> | ||
| Line 50: | Line 73: | ||
</wikitex> | </wikitex> | ||
| − | == | + | == Further discussion == |
<wikitex>; | <wikitex>; | ||
| − | + | </nowikitex> | |
| − | + | ||
| − | + | ||
| − | </ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
== References == | == References == | ||
Revision as of 15:55, 7 June 2010
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Let 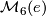 be the set of diffeomorphism classes of closed, oriented, smooth, simply-connected 6-manifolds
be the set of diffeomorphism classes of closed, oriented, smooth, simply-connected 6-manifolds  . Similarly, let
. Similarly, let 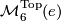 be the set of homeomorphism classes of closed, oriented topological manifolds.
In this article we report on the calculation of
be the set of homeomorphism classes of closed, oriented topological manifolds.
In this article we report on the calculation of 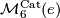 and
and 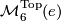 begun by Smale, extended by Wall and Jupp and completed by Zhubr. We shall write
begun by Smale, extended by Wall and Jupp and completed by Zhubr. We shall write 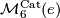 for either
for either 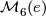 or
or 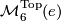 .
.
2 Examples and constructions
We first present some familiar 6-manifolds.
-
 , the standard 6-sphere.
, the standard 6-sphere.
-
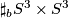 , the
, the  -fold connected sum of
-fold connected sum of Tex syntax error
. -
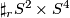 , the
, the  -fold connected sum of
-fold connected sum of 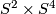 .
.
-
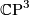 , 3-dimensional complex projective space.
, 3-dimensional complex projective space.
-
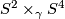 , the non-trivial linear 4-sphere bundle over
, the non-trivial linear 4-sphere bundle over  .
.
- For each
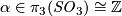 we have
we have 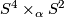 , the corresponding 2-sphere bundle over
, the corresponding 2-sphere bundle over  . If we write 1 for a generator of
. If we write 1 for a generator of 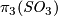 then
then 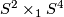 is diffeomorphic to
is diffeomorphic to 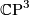 .
.
Surgery on framed links. Let 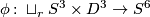 be a framed link. Then
be a framed link. Then 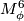 , the outcome of surgery on
, the outcome of surgery on  , is a simply connected Spinable 6-manifold with
, is a simply connected Spinable 6-manifold with 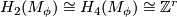 and
and 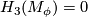 .
.
- ??? Complete intersections of some form.
1 Invariants
The second Stiefel-Whitney class of  is an element of
is an element of 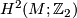 which we regard as a homomorphism
which we regard as a homomorphism 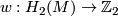 .
.
- The first Pontrjagin class
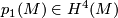 .
.
- The Kirby-Siebenmann class
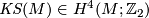
- The cup product
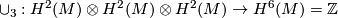 .
.
These invariants satisfy the following relation
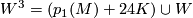
for all 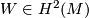 which reduce to
which reduce to 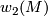 mod
mod  and for all
and for all 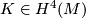 which reduce to
which reduce to 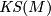 mod
mod  .
.
2 Classification
2.1 Preliminaries
Let 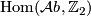 be the set of isomorphism classes of pairs
be the set of isomorphism classes of pairs 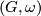 where
where  is a finitely generated abelian group
is a finitely generated abelian group 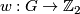 is a homomorphism and where an isomorphism is an isomorphism of groups commuting with the homomorphisms to
is a homomorphism and where an isomorphism is an isomorphism of groups commuting with the homomorphisms to  . The second Stiefel-Whitney classes defines a surjection
. The second Stiefel-Whitney classes defines a surjection
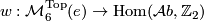
and we let ![\mathcal{M}^{\Cat}_6(G, w) = w^{-1}([G, w])](/images/math/8/0/c/80c4ca5b3295d1266199cb14719c7754.png) denote the set of isomorphism classes of 6-manifolds with prescribed second Stiefel-Whitney class. We obtain the decomposition
denote the set of isomorphism classes of 6-manifolds with prescribed second Stiefel-Whitney class. We obtain the decomposition
![\displaystyle \mathcal{M}^{\Cat}_{6}(e) = \cup_{[G, w]} \mathcal{M}^{\Cat}_{6}(G, w)](/images/math/b/c/4/bc42f0b862f212b051befba26a41415e.png)
where ![[G, w]](/images/math/9/e/1/9e1553e9793f5bee0f5d92936aa7c277.png) ranges over all of
ranges over all of 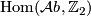 .
.
2.1 The splitting Theorem
Theorem 3 8.1 (Wall).
Let  be a closed, smooth, simply-connected 6-manifold with
be a closed, smooth, simply-connected 6-manifold with 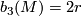 . Then up to diffeomorphism, there is a unique maniofld
. Then up to diffeomorphism, there is a unique maniofld  with
with 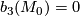 such that
such that  is diffeomorphic to
is diffeomorphic to 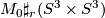 .
.
2.2 Smoothing theory
Theorem 1 8.2.
Let  be a simply-connected, topological 6-manifold. The Kirby-Siebenmann class,
be a simply-connected, topological 6-manifold. The Kirby-Siebenmann class, 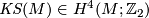 is the sole obstruction to
is the sole obstruction to  admitting a smooth structure.
admitting a smooth structure.
Theorem 2 8.3.
Every homeomorphism 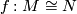 of simply-connected, smooth
of simply-connected, smooth  -manifolds is topologically isotopic to a diffeomorphism. Hence we have an injection
-manifolds is topologically isotopic to a diffeomorphism. Hence we have an injection
Tex syntax error
3 6-manifolds with torsion free second homology
4 2-connected 6-manifolds
 or a connected sum
or a connected sum 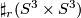 . Hence if
. Hence if 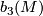 denotes the third Betti-number of
denotes the third Betti-number of  and
and Tex syntax errordenotes the natural numbers we obtain a bijection
Tex syntax error
Applying Theorems 1 and 2 we see that the same statement holds for 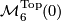 .
.
5 Further discussion
</nowikitex>
References
- [Jupp1973] P. E. Jupp, Classification of certain
 -manifolds, Proc. Cambridge Philos. Soc. 73 (1973), 293–300. MR0314074 (47 #2626) Zbl 0249.57005
-manifolds, Proc. Cambridge Philos. Soc. 73 (1973), 293–300. MR0314074 (47 #2626) Zbl 0249.57005
- [Wall1966] C. T. C. Wall, Classification problems in differential topology. V. On certain
 -manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601
-manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601