5-manifolds with fundamental group of order 2
(→Introduction) |
(→Construction and examples) |
||
| Line 13: | Line 13: | ||
== Construction and examples == | == Construction and examples == | ||
| + | === Circle bundles over simply-connected 4-manifolds === | ||
<wikitex>; | <wikitex>; | ||
| − | ... | + | |
| + | Let $X^4$ be a simply-connected 4-manifold, $\xi$ be a complex line bundle over $X$ with Chern class $c_1(\xi) \in H^2(X;\Zz)$. Let the divisibility of $c_1(\xi)$ be $k$ (i.e. $c_1(\xi)$ is $k$ multiple of a primitive element in $H^2(X;\Zz)$, then the sphere bundle $S(\xi) = \colon M$ is a 5-manifold with fundament group $\Zz_k$ and $\pi_2(M)$ is a free abelian group of rank $\mathrm{rank} H_2(X)-1$, and $\pi_2(M)$ is a trivial module over the group ring. | ||
| + | * $k=1$, $M$ is a simply-connected 5-manifold. The identification of $M$ with manifolds in the standard list of simply-connected 5-manifolds given by the Smale-Barden classification was done in \cite{Duan&Liang}. | ||
| + | * $k=2$, we have a class of 5-manifolds with fundamental group $\Zz_2$, $\pi_2(M)$ a free abelian group, and a trivial module over the group ring. The classification of these manifolds was the motivation of \cite{Hambleton&Su}. | ||
</wikitex> | </wikitex> | ||
Revision as of 13:32, 3 June 2012
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
The classification of simply-connected 5-manifolds was achieved by Smale [Smale] and Barden [Barden] in the 1960s. The surgery and modified surgery theories provide a toolkit to attack the classification problem of high dimensional manifolds. Dimension 5 is the lowest dimension where the theories apply (except for the 4-dimensional TOP-category), therefore an understanding of the classification of 5-manifolds beyond the Smale-Barden results is expectable. On the other hand, it's known ([Markov], [Kervaire]) that every finitely generated group can be realized as the fundamental group of a manifold of dimension  4. Therefore, a practical approach towards the classification of 5-manifolds is to fix a fundamental in advance and consider the classification of manifolds with the given fundamental group.
4. Therefore, a practical approach towards the classification of 5-manifolds is to fix a fundamental in advance and consider the classification of manifolds with the given fundamental group.
Tex syntax error, which is the simplest nontrivial group since it has the least number of elements. (Of course if we take the point of view of generators and relations the rank 1 free group
 is the simplest one.)
is the simplest one.)
Anyother point one should take into account concerning the classification of manifolds with nontrivial fundamental groups 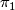 is that the higher homotopy groups
is that the higher homotopy groups 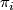 (
(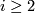 ) are modules over the group ring
) are modules over the group ring ![\Zz[\pi_1]](/images/math/c/b/b/cbbd81afbce9307ff44a102af615c005.png) , which are apparently homotopy invariants. Especially when we consider
, which are apparently homotopy invariants. Especially when we consider 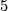 -manifolds
-manifolds 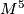 , the
, the ![\Zz[\pi_1]](/images/math/c/b/b/cbbd81afbce9307ff44a102af615c005.png) -module structure of
-module structure of 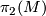 will play an important role in the classification. And it's not a surprise that the first clear classification result obtained is the trivial module case.
will play an important role in the classification. And it's not a surprise that the first clear classification result obtained is the trivial module case.
Most part of this item will be a survey of the classification result of 5-manifolds 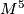 with fundamental group
with fundamental group 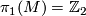 ,
, 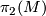 torsion free and is a trivial
torsion free and is a trivial ![\Zz[\Zz_2]](/images/math/0/6/e/06e45b437bee7ce0e2224a3e03e368b4.png) -module obtained in [Hambleton&Su] .
-module obtained in [Hambleton&Su] .
2 Construction and examples
2.1 Circle bundles over simply-connected 4-manifolds
Let 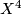 be a simply-connected 4-manifold,
be a simply-connected 4-manifold,  be a complex line bundle over
be a complex line bundle over  with Chern class
with Chern class 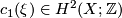 . Let the divisibility of
. Let the divisibility of 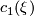 be
be  (i.e.
(i.e. 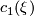 is
is  multiple of a primitive element in
multiple of a primitive element in 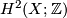 , then the sphere bundle
, then the sphere bundle 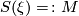 is a 5-manifold with fundament group
is a 5-manifold with fundament group 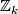 and
and 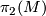 is a free abelian group of rank
is a free abelian group of rank 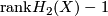 , and
, and 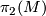 is a trivial module over the group ring.
is a trivial module over the group ring.
-
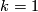 ,
,  is a simply-connected 5-manifold. The identification of
is a simply-connected 5-manifold. The identification of  with manifolds in the standard list of simply-connected 5-manifolds given by the Smale-Barden classification was done in [Duan&Liang].
with manifolds in the standard list of simply-connected 5-manifolds given by the Smale-Barden classification was done in [Duan&Liang].
-
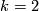 , we have a class of 5-manifolds with fundamental group
, we have a class of 5-manifolds with fundamental group Tex syntax error
,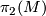 a free abelian group, and a trivial module over the group ring. The classification of these manifolds was the motivation of [Hambleton&Su].
a free abelian group, and a trivial module over the group ring. The classification of these manifolds was the motivation of [Hambleton&Su].
3 Invariants
...
4 Classification/Characterization
...
5 Further discussion
...