5-manifolds: 1-connected
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:22, 1 April 2011 and the changes since publication. |
Let 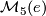 be the set of diffeomorphism classes of closed, oriented, smooth, simply-connected 5-manifolds
be the set of diffeomorphism classes of closed, oriented, smooth, simply-connected 5-manifolds  and let
and let 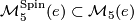 be the subset of diffeomorphism classes of spinable manifolds. In this article we report the calculation of
be the subset of diffeomorphism classes of spinable manifolds. In this article we report the calculation of 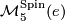 first obtained in [Smale1962] and of
first obtained in [Smale1962] and of  first obtained in general in [Barden1965].
first obtained in general in [Barden1965].
Contents |
1 Constructions and examples
We first list some familiar 5-manifolds using Barden's notation:
-
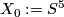
-
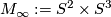
-
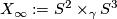 , the total space of the non-trivial
, the total space of the non-trivial  -bundle over
-bundle over 
-
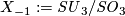 , the Wu-manifold, is the homogeneous space obtained from the standadard inclusion of
, the Wu-manifold, is the homogeneous space obtained from the standadard inclusion of 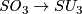 .
.
Next we present a construction of Spin 5-manifolds. Note that all homology groups are with integer coefficients. Given a finitely generated abelian group  , let
, let 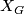 denote the degree 2 Moore space with
denote the degree 2 Moore space with 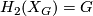 . The space
. The space 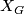 may be realised as a finite CW-complex and so there is an embedding
may be realised as a finite CW-complex and so there is an embedding 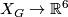 . Let
. Let 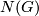 be a regular neighbourhood of
be a regular neighbourhood of 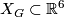 and let
and let 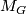 be the boundary of
be the boundary of 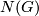 . Then
. Then 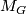 is a closed, smooth, simply-connected, spinable 5-manifold with
is a closed, smooth, simply-connected, spinable 5-manifold with  where
where 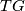 is the torsion subgroup of
is the torsion subgroup of  . For example,
. For example, 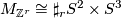 where
where 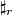 denotes the
denotes the  -fold connected sum.
-fold connected sum.
For the non-Spin case let 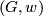 be a pair with
be a pair with 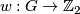 a surjective homomorphism and
a surjective homomorphism and  as above. We shall construct a non-Spin 5-manifold
as above. We shall construct a non-Spin 5-manifold 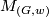 with
with 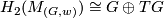 and second Stiefel-Whitney class
and second Stiefel-Whitney class 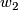 given by
given by  composed with the projection
composed with the projection 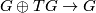 . If
. If 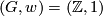 let
let 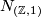 be the non-trivial
be the non-trivial 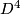 -bundle over
-bundle over  with boundary
with boundary 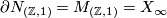 . If
. If 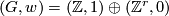 let
let 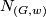 be the boundary connected sum
be the boundary connected sum 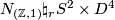 with boundary
with boundary 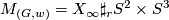 . In the general case, present
. In the general case, present 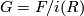 where
where 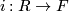 is an injective homomorphism between free abelian groups. Lift
is an injective homomorphism between free abelian groups. Lift 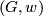 to
to 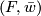 and observe that there is a canonical identification
and observe that there is a canonical identification 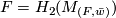 . If
. If 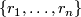 is a basis for
is a basis for  note that each
note that each 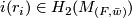 is represented by a an embedded 2-sphere with trivial normal bundle. Let
is represented by a an embedded 2-sphere with trivial normal bundle. Let 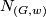 be the manifold obtained by attaching 3-handles to
be the manifold obtained by attaching 3-handles to 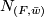 along spheres representing
along spheres representing 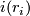 and let
and let 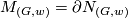 . One may check that
. One may check that 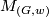 is a non-Spin manifold as described above.
is a non-Spin manifold as described above.
- !!! To do: determine which 1-connected 5-manifolds appear as Brieskorn varieties.
2 Invariants
Consider the following invariants of a closed simply-connected 5-manifold  .
.
-
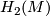 be the second integral homology group of
be the second integral homology group of  , with torsion subgroup
, with torsion subgroup 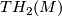 .
.
-
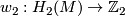 , the homomorphism defined by evaluation with the second Stiefel-Whitney class of
, the homomorphism defined by evaluation with the second Stiefel-Whitney class of  ,
, 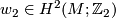 .
.
-
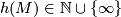 , the smallest extended natural number
, the smallest extended natural number  such that
such that 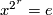 and
and 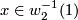 . If
. If  is Spin we set
is Spin we set 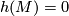 .
.
-
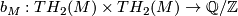 , the linking form of
, the linking form of  which is a non-singular anti-symmetric bi-linear pairing on
which is a non-singular anti-symmetric bi-linear pairing on 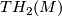 .
.
By [Wall1962, Proposition 1 & 2] the linking form satisfies the identity 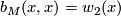 where we regard
where we regard 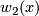 as an element of
as an element of 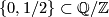 .
.
For example, the Wu-manifold 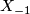 has
has 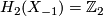 , non-trivial
, non-trivial 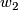 and
and 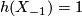 .
.
An abstract non-singular, anti-symmetric linking form 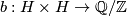 on a finite group
on a finite group  is a bi-linear function such that
is a bi-linear function such that 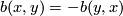 and
and 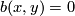 for all
for all 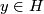 if and only if
if and only if 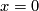 . By [Wall1963] such linking forms are classified up to isomorphism by the homomorphism
. By [Wall1963] such linking forms are classified up to isomorphism by the homomorphism 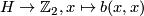 . Moreover
. Moreover  must be isomorphic to
must be isomorphic to 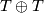 or
or 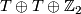 for some finite group
for some finite group  with
with 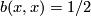 if
if  generates the
generates the  summand. In particular the second Stiefel-Whitney class of a 5-manifold
summand. In particular the second Stiefel-Whitney class of a 5-manifold  determines the isomorphism class of the linking form
determines the isomorphism class of the linking form 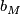 and we see that the torsion subgroup of
and we see that the torsion subgroup of 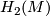 is of the form
is of the form 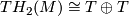 if
if 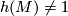 or
or 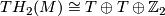 if
if 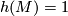 in which case the
in which case the  summand is an orthogonal summand of
summand is an orthogonal summand of 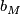 .
.
3 Classification
We first present the most economical classifications of  and
and 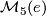 . Let
. Let 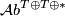 be the set of isomorphism classes finitely generated abelian groups
be the set of isomorphism classes finitely generated abelian groups  with torsion subgroup
with torsion subgroup 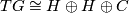 where
where  is trivial or
is trivial or 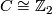 and write
and write 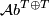 and
and 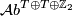 for the obvious subsets.
for the obvious subsets.
![\displaystyle \mathcal{M}_5^{\Spin}(e) \rightarrow {\mathcal Ab}^{T\oplus T}, \quad [M] \mapsto [H_2(M)].](/images/math/9/7/9/97990582a2b53b495de72945c621e72f.png)
Theorem 3.2 [Barden1965]. The mapping
![\displaystyle \mathcal{M}_{5}(e) \rightarrow {\mathcal Ab}^{T \oplus T \oplus *} \times (\Nn \cup \{ \infty \}) , \quad [M] \mapsto ([H_2(M)], h(M))](/images/math/4/8/5/4855c33282a2801dab46d98157d124ae.png)
is an injection onto the subset of pairs ![([G], n)](/images/math/0/6/6/066c10d7231c9606db2b9be060eb18f6.png) where
where ![[G] \in {\mathcal Ab}^{T \oplus T \oplus \Zz_2}](/images/math/d/5/a/d5adb9bd1c6cad846bec22c61be697f0.png) if and only if
if and only if 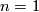 .
.
The above theorems follow from the following theorem of Barden and the classification of anti-symmetric linking forms.
Theorem 3.3 [Barden1965, Theorem 2.2]. Let  and
and  be simply-connected, closed, smooth 5-manifolds and let
be simply-connected, closed, smooth 5-manifolds and let 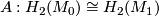 be an isomorphism preserving the linking form and the second Stiefel-Whitney class. Then
be an isomorphism preserving the linking form and the second Stiefel-Whitney class. Then  is realised by a diffeomorphism.
is realised by a diffeomorphism.
This theorem can re-phrased in categorical language as follows: let 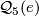 be a small category, in fact groupoid, with objects
be a small category, in fact groupoid, with objects 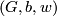 where
where  is a finitely generated abelian group,
is a finitely generated abelian group, 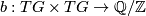 is a anti-symmetric non-singular linking form and
is a anti-symmetric non-singular linking form and 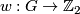 is a homomorphism such that
is a homomorphism such that 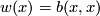 for all
for all 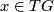 . The morphisms of
. The morphisms of 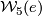 are isomorphisms of abelian groups commuting with both
are isomorphisms of abelian groups commuting with both  and
and  .
.
Now let 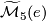 be a small category, actually groupoid, with objects simply-connected, closed, smooth 5-manifolds and morphisms isotopy diffeomorphisms. Let
be a small category, actually groupoid, with objects simply-connected, closed, smooth 5-manifolds and morphisms isotopy diffeomorphisms. Let 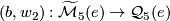 be the funtor which maps
be the funtor which maps  to
to 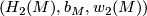 and
and 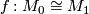 to the induced map on
to the induced map on 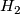 .
.
Theorem [Barden1965] 3.4. The functor
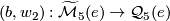
is a detecting functor. That is, it is surjective on objects and 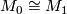 if and only if
if and only if 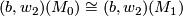 .
.
3.1 Enumeration
We give Barden's enumeration of the set 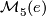 , [Barden1965, Theorem 2.3].
, [Barden1965, Theorem 2.3].
-
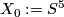 ,
, 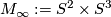 ,
, 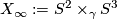 ,
, 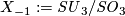 .
.
- For
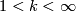 ,
, 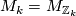 is the Spin manifold with
is the Spin manifold with 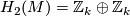 constructed above.
constructed above.
- For
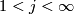 let
let 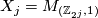 constructed above be the non-Spin manifold with
constructed above be the non-Spin manifold with 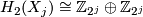 .
.
With this notation [Barden1965, Theorem 2.3] states that a complete list of diffeomorphism classes of simply-connected 5-manifolds is given by
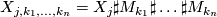
where 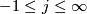 ,
, 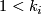 ,
, 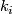 divides
divides 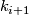 or
or 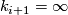 and
and  denotes the connected sum of oriented manifolds. The manifold
denotes the connected sum of oriented manifolds. The manifold 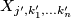 is diffeomorphic to
is diffeomorphic to 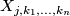 if and only if
if and only if 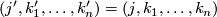 .
.
An alternative complete enumeration is obtained by writing 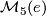 as a disjoint union
as a disjoint union
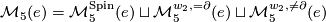
![\displaystyle \mathcal{M}_5^{\Spin}(e) = \{ [M_G] \}, ~~\mathcal{M}_5^{w_2, = \partial}(e) = \{ [M_{(G, \omega)}] \} ~~\text{and}~~ \mathcal{M}_5^{w_2, \neq \partial}(e) = \{ [ X_{-1} \sharp M_G] \}.](/images/math/7/d/b/7db70491f84c955347708c8b9f01004f.png)
4 Further discussion
- As the invariants which classify closed, oriented 5-manifolds are homotopy invariants, we see that the same classification holds up to homotopy, homeomorphism and piecewise linear homeomorphism.
- The classification of simply-connected Spin 5-manifolds was one of the first applications of the h-cobordism theorem.
- By the construction above every simply-connected, closed, smooth, Spin 5-manifold embedds into
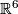 .
.
- As the invariants for
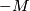 are isomorphic to the invariants of
are isomorphic to the invariants of  we see that every smooth 5-manifold admits an orientation reversing diffeomorphism: i.e. all 5-manifolds are smoothly amphicheiral.
we see that every smooth 5-manifold admits an orientation reversing diffeomorphism: i.e. all 5-manifolds are smoothly amphicheiral.
4.1 Bordism groups
As ![\mathcal{M}_5^{\Spin}(e) = \{[M_G]\}](/images/math/f/b/7/fb7063131a17d2e0dd1e2500231179b6.png) and
and 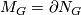 we see that every closed, Spin 5-manifold bounds a Spin 6-manifold. Hence the bordism group
we see that every closed, Spin 5-manifold bounds a Spin 6-manifold. Hence the bordism group 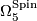 vanishes.
vanishes.
The bordism group 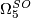 is isomorphic to
is isomorphic to  and is detected by the Stiefel-Whitney number
and is detected by the Stiefel-Whitney number ![\langle w_2(M)w_3(M), [M] \rangle \in \Zz_2](/images/math/9/b/9/9b9476a5ddc2349bc6380f1e03304d99.png) . The Wu-manifold has cohomology groups
. The Wu-manifold has cohomology groups
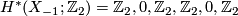
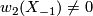 . It follows that
. It follows that 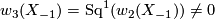 and that
and that ![\langle w_2(X_{-1})w_3(X_{-1}), [X_{-1}] \rangle \neq 0](/images/math/8/2/1/821189f95965b9293938b9750b268abc.png) . We see that
. We see that ![[X_{-1}]](/images/math/3/f/3/3f3bed6681734999df212ea7e3e6b26d.png) is the generator of
is the generator of 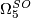 and that a closed, smooth 5-manifold
and that a closed, smooth 5-manifold  is not a boundary if and only if it is diffeomorphic to
is not a boundary if and only if it is diffeomorphic to 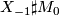 where
where  is a Spin manifold.
is a Spin manifold.
- !!! Add references here.
4.2 Curvature and contact structures
- Every manifold
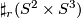 admits a metric of positive Ricci curvature [Boyer&Galicki2006].
admits a metric of positive Ricci curvature [Boyer&Galicki2006].
- Every Spin 5-manifold with the order of
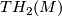 prime to 3 admits a contact structure [Thomas1986].
prime to 3 admits a contact structure [Thomas1986].
4.3 Mapping class groups
Let 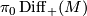 denote the group of isotopy classes of orientation preserving diffeomorphisms
denote the group of isotopy classes of orientation preserving diffeomorphisms 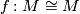 and let
and let 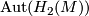 be the group of isomorphisms of
be the group of isomorphisms of 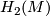 preserving the linking form and the second Stiefel-Whitney class. Applying the second statement of Barden's classification above
we obtain an exact sequence
preserving the linking form and the second Stiefel-Whitney class. Applying the second statement of Barden's classification above
we obtain an exact sequence
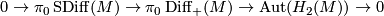
where 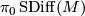 is the group of isotopy classes of diffeomorphisms inducing the identity on
is the group of isotopy classes of diffeomorphisms inducing the identity on 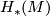 .
.
- Open problem: as of writing there is no computation of
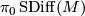 for a general simply-connected 5-manifold.
for a general simply-connected 5-manifold.
- The isotopy group
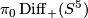 is known to be the trivial group [[[#|]]].
is known to be the trivial group [[[#|]]].
- In the homotopy category,
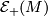 , the group of homotopy classes of orientation preserving homotopy equivalences of
, the group of homotopy classes of orientation preserving homotopy equivalences of  , has been extensively investigated by [Baues&Buth1996] and is already seen to be relatively complex.
, has been extensively investigated by [Baues&Buth1996] and is already seen to be relatively complex.
5 References
- [Baues&Buth1996] H. J. Baues and J. Buth, On the group of homotopy equivalences of simply connected five manifolds, Math. Z. 222 (1996), no.4, 573–614. MR1406269 (97g:55009) Zbl 0881.55008
- [Barden1965] D. Barden, Simply connected five-manifolds, Ann. of Math. (2) 82 (1965), 365–385. MR0184241 (32 #1714) Zbl 0136.20602
- [Boyer&Galicki2006] C. P. Boyer and K. Galicki, Highly connected manifolds with positive Ricci curvature, Geom. Topol. 10 (2006), 2219–2235 (electronic). MR2284055 (2007k:53057) Zbl 1129.53026
- [Smale1962] S. Smale, On the structure of
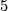 -manifolds, Ann. of Math. (2) 75 (1962), 38–46. MR0141133 (25 #4544) Zbl 0101.16103
-manifolds, Ann. of Math. (2) 75 (1962), 38–46. MR0141133 (25 #4544) Zbl 0101.16103
- [Thomas1986] C. B. Thomas, Contact structures on
 -connected
-connected 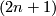 -manifolds, 18 (1986), 255–270. MR925869 (89b:53074) Zbl 0642.57014
-manifolds, 18 (1986), 255–270. MR925869 (89b:53074) Zbl 0642.57014
- [Wall1962] C. T. C. Wall, Killing the middle homotopy groups of odd dimensional manifolds, Trans. Amer. Math. Soc. 103 (1962), 421–433. MR0139185 (25 #2621) Zbl 0199.26803
- [Wall1963] C. T. C. Wall, Quadratic forms on finite groups, and related topics, Topology 2 (1963), 281–298. MR0156890 (28 #133) Zbl 0215.39903MediaWiki:Stub
 and let
and let 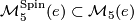 be the subset of diffeomorphism classes of spinable manifolds. In this article we report the calculation of
be the subset of diffeomorphism classes of spinable manifolds. In this article we report the calculation of 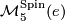 first obtained in [Smale1962] and of
first obtained in [Smale1962] and of 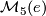 first obtained in general in [Barden1965].
first obtained in general in [Barden1965].
Contents |
1 Constructions and examples
We first list some familiar 5-manifolds using Barden's notation:
-
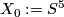
-
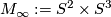
-
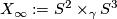 , the total space of the non-trivial
, the total space of the non-trivial  -bundle over
-bundle over 
-
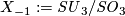 , the Wu-manifold, is the homogeneous space obtained from the standadard inclusion of
, the Wu-manifold, is the homogeneous space obtained from the standadard inclusion of 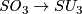 .
.
Next we present a construction of Spin 5-manifolds. Note that all homology groups are with integer coefficients. Given a finitely generated abelian group  , let
, let 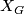 denote the degree 2 Moore space with
denote the degree 2 Moore space with 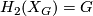 . The space
. The space 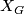 may be realised as a finite CW-complex and so there is an embedding
may be realised as a finite CW-complex and so there is an embedding 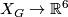 . Let
. Let 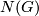 be a regular neighbourhood of
be a regular neighbourhood of 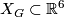 and let
and let 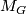 be the boundary of
be the boundary of 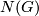 . Then
. Then 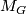 is a closed, smooth, simply-connected, spinable 5-manifold with
is a closed, smooth, simply-connected, spinable 5-manifold with  where
where 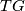 is the torsion subgroup of
is the torsion subgroup of  . For example,
. For example, 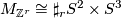 where
where 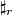 denotes the
denotes the  -fold connected sum.
-fold connected sum.
For the non-Spin case let 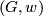 be a pair with
be a pair with 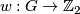 a surjective homomorphism and
a surjective homomorphism and  as above. We shall construct a non-Spin 5-manifold
as above. We shall construct a non-Spin 5-manifold 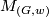 with
with 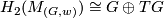 and second Stiefel-Whitney class
and second Stiefel-Whitney class 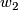 given by
given by  composed with the projection
composed with the projection 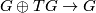 . If
. If 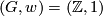 let
let 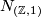 be the non-trivial
be the non-trivial 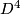 -bundle over
-bundle over  with boundary
with boundary 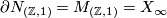 . If
. If 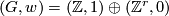 let
let 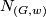 be the boundary connected sum
be the boundary connected sum 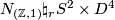 with boundary
with boundary 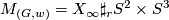 . In the general case, present
. In the general case, present 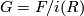 where
where 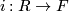 is an injective homomorphism between free abelian groups. Lift
is an injective homomorphism between free abelian groups. Lift 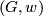 to
to 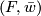 and observe that there is a canonical identification
and observe that there is a canonical identification 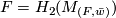 . If
. If 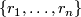 is a basis for
is a basis for  note that each
note that each 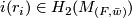 is represented by a an embedded 2-sphere with trivial normal bundle. Let
is represented by a an embedded 2-sphere with trivial normal bundle. Let 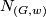 be the manifold obtained by attaching 3-handles to
be the manifold obtained by attaching 3-handles to 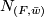 along spheres representing
along spheres representing 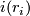 and let
and let 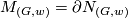 . One may check that
. One may check that 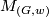 is a non-Spin manifold as described above.
is a non-Spin manifold as described above.
- !!! To do: determine which 1-connected 5-manifolds appear as Brieskorn varieties.
2 Invariants
Consider the following invariants of a closed simply-connected 5-manifold  .
.
-
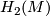 be the second integral homology group of
be the second integral homology group of  , with torsion subgroup
, with torsion subgroup 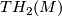 .
.
-
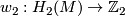 , the homomorphism defined by evaluation with the second Stiefel-Whitney class of
, the homomorphism defined by evaluation with the second Stiefel-Whitney class of  ,
, 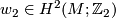 .
.
-
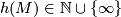 , the smallest extended natural number
, the smallest extended natural number  such that
such that 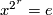 and
and 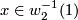 . If
. If  is Spin we set
is Spin we set 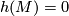 .
.
-
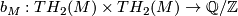 , the linking form of
, the linking form of  which is a non-singular anti-symmetric bi-linear pairing on
which is a non-singular anti-symmetric bi-linear pairing on 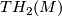 .
.
By [Wall1962, Proposition 1 & 2] the linking form satisfies the identity 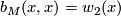 where we regard
where we regard 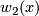 as an element of
as an element of 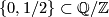 .
.
For example, the Wu-manifold 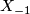 has
has 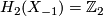 , non-trivial
, non-trivial 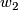 and
and 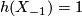 .
.
An abstract non-singular, anti-symmetric linking form 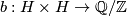 on a finite group
on a finite group  is a bi-linear function such that
is a bi-linear function such that 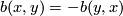 and
and 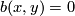 for all
for all 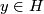 if and only if
if and only if 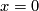 . By [Wall1963] such linking forms are classified up to isomorphism by the homomorphism
. By [Wall1963] such linking forms are classified up to isomorphism by the homomorphism 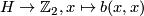 . Moreover
. Moreover  must be isomorphic to
must be isomorphic to 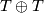 or
or 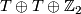 for some finite group
for some finite group  with
with 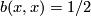 if
if  generates the
generates the  summand. In particular the second Stiefel-Whitney class of a 5-manifold
summand. In particular the second Stiefel-Whitney class of a 5-manifold  determines the isomorphism class of the linking form
determines the isomorphism class of the linking form 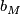 and we see that the torsion subgroup of
and we see that the torsion subgroup of 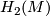 is of the form
is of the form 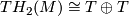 if
if 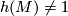 or
or 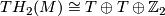 if
if 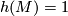 in which case the
in which case the  summand is an orthogonal summand of
summand is an orthogonal summand of 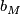 .
.
3 Classification
We first present the most economical classifications of  and
and 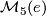 . Let
. Let 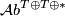 be the set of isomorphism classes finitely generated abelian groups
be the set of isomorphism classes finitely generated abelian groups  with torsion subgroup
with torsion subgroup 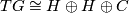 where
where  is trivial or
is trivial or 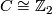 and write
and write 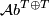 and
and 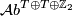 for the obvious subsets.
for the obvious subsets.
![\displaystyle \mathcal{M}_5^{\Spin}(e) \rightarrow {\mathcal Ab}^{T\oplus T}, \quad [M] \mapsto [H_2(M)].](/images/math/9/7/9/97990582a2b53b495de72945c621e72f.png)
Theorem 3.2 [Barden1965]. The mapping
![\displaystyle \mathcal{M}_{5}(e) \rightarrow {\mathcal Ab}^{T \oplus T \oplus *} \times (\Nn \cup \{ \infty \}) , \quad [M] \mapsto ([H_2(M)], h(M))](/images/math/4/8/5/4855c33282a2801dab46d98157d124ae.png)
is an injection onto the subset of pairs ![([G], n)](/images/math/0/6/6/066c10d7231c9606db2b9be060eb18f6.png) where
where ![[G] \in {\mathcal Ab}^{T \oplus T \oplus \Zz_2}](/images/math/d/5/a/d5adb9bd1c6cad846bec22c61be697f0.png) if and only if
if and only if 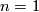 .
.
The above theorems follow from the following theorem of Barden and the classification of anti-symmetric linking forms.
Theorem 3.3 [Barden1965, Theorem 2.2]. Let  and
and  be simply-connected, closed, smooth 5-manifolds and let
be simply-connected, closed, smooth 5-manifolds and let 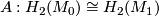 be an isomorphism preserving the linking form and the second Stiefel-Whitney class. Then
be an isomorphism preserving the linking form and the second Stiefel-Whitney class. Then  is realised by a diffeomorphism.
is realised by a diffeomorphism.
This theorem can re-phrased in categorical language as follows: let 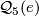 be a small category, in fact groupoid, with objects
be a small category, in fact groupoid, with objects 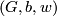 where
where  is a finitely generated abelian group,
is a finitely generated abelian group, 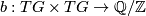 is a anti-symmetric non-singular linking form and
is a anti-symmetric non-singular linking form and 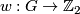 is a homomorphism such that
is a homomorphism such that 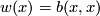 for all
for all 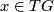 . The morphisms of
. The morphisms of 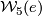 are isomorphisms of abelian groups commuting with both
are isomorphisms of abelian groups commuting with both  and
and  .
.
Now let 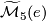 be a small category, actually groupoid, with objects simply-connected, closed, smooth 5-manifolds and morphisms isotopy diffeomorphisms. Let
be a small category, actually groupoid, with objects simply-connected, closed, smooth 5-manifolds and morphisms isotopy diffeomorphisms. Let 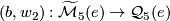 be the funtor which maps
be the funtor which maps  to
to 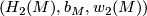 and
and 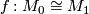 to the induced map on
to the induced map on 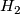 .
.
Theorem [Barden1965] 3.4. The functor
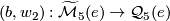
is a detecting functor. That is, it is surjective on objects and 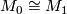 if and only if
if and only if 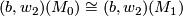 .
.
3.1 Enumeration
We give Barden's enumeration of the set 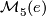 , [Barden1965, Theorem 2.3].
, [Barden1965, Theorem 2.3].
-
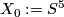 ,
, 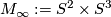 ,
, 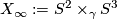 ,
, 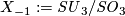 .
.
- For
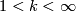 ,
, 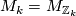 is the Spin manifold with
is the Spin manifold with 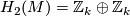 constructed above.
constructed above.
- For
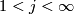 let
let 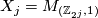 constructed above be the non-Spin manifold with
constructed above be the non-Spin manifold with 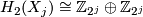 .
.
With this notation [Barden1965, Theorem 2.3] states that a complete list of diffeomorphism classes of simply-connected 5-manifolds is given by
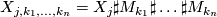
where 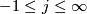 ,
, 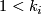 ,
, 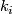 divides
divides 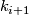 or
or 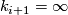 and
and  denotes the connected sum of oriented manifolds. The manifold
denotes the connected sum of oriented manifolds. The manifold 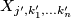 is diffeomorphic to
is diffeomorphic to 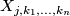 if and only if
if and only if 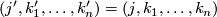 .
.
An alternative complete enumeration is obtained by writing 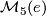 as a disjoint union
as a disjoint union
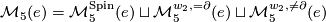
![\displaystyle \mathcal{M}_5^{\Spin}(e) = \{ [M_G] \}, ~~\mathcal{M}_5^{w_2, = \partial}(e) = \{ [M_{(G, \omega)}] \} ~~\text{and}~~ \mathcal{M}_5^{w_2, \neq \partial}(e) = \{ [ X_{-1} \sharp M_G] \}.](/images/math/7/d/b/7db70491f84c955347708c8b9f01004f.png)
4 Further discussion
- As the invariants which classify closed, oriented 5-manifolds are homotopy invariants, we see that the same classification holds up to homotopy, homeomorphism and piecewise linear homeomorphism.
- The classification of simply-connected Spin 5-manifolds was one of the first applications of the h-cobordism theorem.
- By the construction above every simply-connected, closed, smooth, Spin 5-manifold embedds into
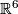 .
.
- As the invariants for
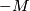 are isomorphic to the invariants of
are isomorphic to the invariants of  we see that every smooth 5-manifold admits an orientation reversing diffeomorphism: i.e. all 5-manifolds are smoothly amphicheiral.
we see that every smooth 5-manifold admits an orientation reversing diffeomorphism: i.e. all 5-manifolds are smoothly amphicheiral.
4.1 Bordism groups
As ![\mathcal{M}_5^{\Spin}(e) = \{[M_G]\}](/images/math/f/b/7/fb7063131a17d2e0dd1e2500231179b6.png) and
and 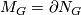 we see that every closed, Spin 5-manifold bounds a Spin 6-manifold. Hence the bordism group
we see that every closed, Spin 5-manifold bounds a Spin 6-manifold. Hence the bordism group 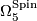 vanishes.
vanishes.
The bordism group 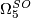 is isomorphic to
is isomorphic to  and is detected by the Stiefel-Whitney number
and is detected by the Stiefel-Whitney number ![\langle w_2(M)w_3(M), [M] \rangle \in \Zz_2](/images/math/9/b/9/9b9476a5ddc2349bc6380f1e03304d99.png) . The Wu-manifold has cohomology groups
. The Wu-manifold has cohomology groups
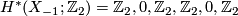
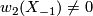 . It follows that
. It follows that 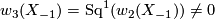 and that
and that ![\langle w_2(X_{-1})w_3(X_{-1}), [X_{-1}] \rangle \neq 0](/images/math/8/2/1/821189f95965b9293938b9750b268abc.png) . We see that
. We see that ![[X_{-1}]](/images/math/3/f/3/3f3bed6681734999df212ea7e3e6b26d.png) is the generator of
is the generator of 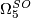 and that a closed, smooth 5-manifold
and that a closed, smooth 5-manifold  is not a boundary if and only if it is diffeomorphic to
is not a boundary if and only if it is diffeomorphic to 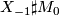 where
where  is a Spin manifold.
is a Spin manifold.
- !!! Add references here.
4.2 Curvature and contact structures
- Every manifold
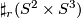 admits a metric of positive Ricci curvature [Boyer&Galicki2006].
admits a metric of positive Ricci curvature [Boyer&Galicki2006].
- Every Spin 5-manifold with the order of
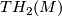 prime to 3 admits a contact structure [Thomas1986].
prime to 3 admits a contact structure [Thomas1986].
4.3 Mapping class groups
Let 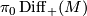 denote the group of isotopy classes of orientation preserving diffeomorphisms
denote the group of isotopy classes of orientation preserving diffeomorphisms 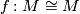 and let
and let 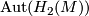 be the group of isomorphisms of
be the group of isomorphisms of 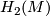 preserving the linking form and the second Stiefel-Whitney class. Applying the second statement of Barden's classification above
we obtain an exact sequence
preserving the linking form and the second Stiefel-Whitney class. Applying the second statement of Barden's classification above
we obtain an exact sequence
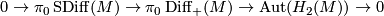
where 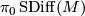 is the group of isotopy classes of diffeomorphisms inducing the identity on
is the group of isotopy classes of diffeomorphisms inducing the identity on 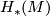 .
.
- Open problem: as of writing there is no computation of
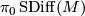 for a general simply-connected 5-manifold.
for a general simply-connected 5-manifold.
- The isotopy group
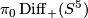 is known to be the trivial group [[[#|]]].
is known to be the trivial group [[[#|]]].
- In the homotopy category,
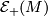 , the group of homotopy classes of orientation preserving homotopy equivalences of
, the group of homotopy classes of orientation preserving homotopy equivalences of  , has been extensively investigated by [Baues&Buth1996] and is already seen to be relatively complex.
, has been extensively investigated by [Baues&Buth1996] and is already seen to be relatively complex.
5 References
- [Baues&Buth1996] H. J. Baues and J. Buth, On the group of homotopy equivalences of simply connected five manifolds, Math. Z. 222 (1996), no.4, 573–614. MR1406269 (97g:55009) Zbl 0881.55008
- [Barden1965] D. Barden, Simply connected five-manifolds, Ann. of Math. (2) 82 (1965), 365–385. MR0184241 (32 #1714) Zbl 0136.20602
- [Boyer&Galicki2006] C. P. Boyer and K. Galicki, Highly connected manifolds with positive Ricci curvature, Geom. Topol. 10 (2006), 2219–2235 (electronic). MR2284055 (2007k:53057) Zbl 1129.53026
- [Smale1962] S. Smale, On the structure of
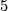 -manifolds, Ann. of Math. (2) 75 (1962), 38–46. MR0141133 (25 #4544) Zbl 0101.16103
-manifolds, Ann. of Math. (2) 75 (1962), 38–46. MR0141133 (25 #4544) Zbl 0101.16103
- [Thomas1986] C. B. Thomas, Contact structures on
 -connected
-connected 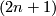 -manifolds, 18 (1986), 255–270. MR925869 (89b:53074) Zbl 0642.57014
-manifolds, 18 (1986), 255–270. MR925869 (89b:53074) Zbl 0642.57014
- [Wall1962] C. T. C. Wall, Killing the middle homotopy groups of odd dimensional manifolds, Trans. Amer. Math. Soc. 103 (1962), 421–433. MR0139185 (25 #2621) Zbl 0199.26803
- [Wall1963] C. T. C. Wall, Quadratic forms on finite groups, and related topics, Topology 2 (1963), 281–298. MR0156890 (28 #133) Zbl 0215.39903MediaWiki:Stub
 and let
and let 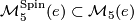 be the subset of diffeomorphism classes of spinable manifolds. In this article we report the calculation of
be the subset of diffeomorphism classes of spinable manifolds. In this article we report the calculation of 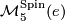 first obtained in [Smale1962] and of
first obtained in [Smale1962] and of 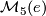 first obtained in general in [Barden1965].
first obtained in general in [Barden1965].
Contents |
1 Constructions and examples
We first list some familiar 5-manifolds using Barden's notation:
-
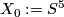
-
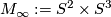
-
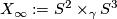 , the total space of the non-trivial
, the total space of the non-trivial  -bundle over
-bundle over 
-
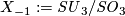 , the Wu-manifold, is the homogeneous space obtained from the standadard inclusion of
, the Wu-manifold, is the homogeneous space obtained from the standadard inclusion of 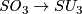 .
.
Next we present a construction of Spin 5-manifolds. Note that all homology groups are with integer coefficients. Given a finitely generated abelian group  , let
, let 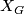 denote the degree 2 Moore space with
denote the degree 2 Moore space with 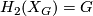 . The space
. The space 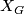 may be realised as a finite CW-complex and so there is an embedding
may be realised as a finite CW-complex and so there is an embedding 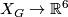 . Let
. Let 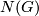 be a regular neighbourhood of
be a regular neighbourhood of 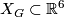 and let
and let 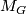 be the boundary of
be the boundary of 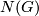 . Then
. Then 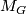 is a closed, smooth, simply-connected, spinable 5-manifold with
is a closed, smooth, simply-connected, spinable 5-manifold with  where
where 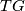 is the torsion subgroup of
is the torsion subgroup of  . For example,
. For example, 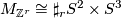 where
where 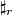 denotes the
denotes the  -fold connected sum.
-fold connected sum.
For the non-Spin case let 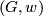 be a pair with
be a pair with 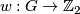 a surjective homomorphism and
a surjective homomorphism and  as above. We shall construct a non-Spin 5-manifold
as above. We shall construct a non-Spin 5-manifold 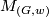 with
with 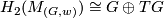 and second Stiefel-Whitney class
and second Stiefel-Whitney class 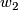 given by
given by  composed with the projection
composed with the projection 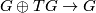 . If
. If 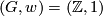 let
let 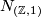 be the non-trivial
be the non-trivial 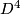 -bundle over
-bundle over  with boundary
with boundary 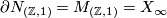 . If
. If 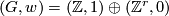 let
let 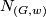 be the boundary connected sum
be the boundary connected sum 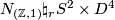 with boundary
with boundary 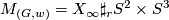 . In the general case, present
. In the general case, present 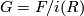 where
where 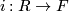 is an injective homomorphism between free abelian groups. Lift
is an injective homomorphism between free abelian groups. Lift 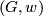 to
to 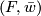 and observe that there is a canonical identification
and observe that there is a canonical identification 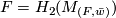 . If
. If 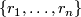 is a basis for
is a basis for  note that each
note that each 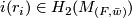 is represented by a an embedded 2-sphere with trivial normal bundle. Let
is represented by a an embedded 2-sphere with trivial normal bundle. Let 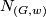 be the manifold obtained by attaching 3-handles to
be the manifold obtained by attaching 3-handles to 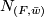 along spheres representing
along spheres representing 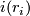 and let
and let 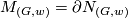 . One may check that
. One may check that 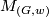 is a non-Spin manifold as described above.
is a non-Spin manifold as described above.
- !!! To do: determine which 1-connected 5-manifolds appear as Brieskorn varieties.
2 Invariants
Consider the following invariants of a closed simply-connected 5-manifold  .
.
-
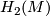 be the second integral homology group of
be the second integral homology group of  , with torsion subgroup
, with torsion subgroup 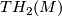 .
.
-
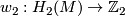 , the homomorphism defined by evaluation with the second Stiefel-Whitney class of
, the homomorphism defined by evaluation with the second Stiefel-Whitney class of  ,
, 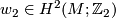 .
.
-
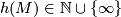 , the smallest extended natural number
, the smallest extended natural number  such that
such that 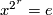 and
and 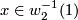 . If
. If  is Spin we set
is Spin we set 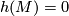 .
.
-
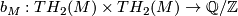 , the linking form of
, the linking form of  which is a non-singular anti-symmetric bi-linear pairing on
which is a non-singular anti-symmetric bi-linear pairing on 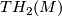 .
.
By [Wall1962, Proposition 1 & 2] the linking form satisfies the identity 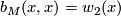 where we regard
where we regard 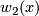 as an element of
as an element of  .
.
For example, the Wu-manifold 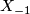 has
has 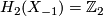 , non-trivial
, non-trivial 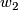 and
and 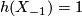 .
.
An abstract non-singular, anti-symmetric linking form 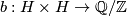 on a finite group
on a finite group  is a bi-linear function such that
is a bi-linear function such that 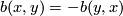 and
and 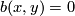 for all
for all 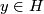 if and only if
if and only if 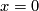 . By [Wall1963] such linking forms are classified up to isomorphism by the homomorphism
. By [Wall1963] such linking forms are classified up to isomorphism by the homomorphism 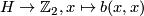 . Moreover
. Moreover  must be isomorphic to
must be isomorphic to 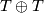 or
or 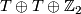 for some finite group
for some finite group  with
with 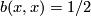 if
if  generates the
generates the  summand. In particular the second Stiefel-Whitney class of a 5-manifold
summand. In particular the second Stiefel-Whitney class of a 5-manifold  determines the isomorphism class of the linking form
determines the isomorphism class of the linking form 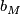 and we see that the torsion subgroup of
and we see that the torsion subgroup of 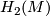 is of the form
is of the form 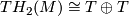 if
if 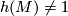 or
or 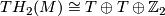 if
if 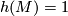 in which case the
in which case the  summand is an orthogonal summand of
summand is an orthogonal summand of 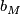 .
.
3 Classification
We first present the most economical classifications of  and
and 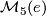 . Let
. Let 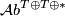 be the set of isomorphism classes finitely generated abelian groups
be the set of isomorphism classes finitely generated abelian groups  with torsion subgroup
with torsion subgroup 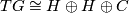 where
where  is trivial or
is trivial or 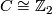 and write
and write 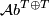 and
and 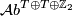 for the obvious subsets.
for the obvious subsets.
![\displaystyle \mathcal{M}_5^{\Spin}(e) \rightarrow {\mathcal Ab}^{T\oplus T}, \quad [M] \mapsto [H_2(M)].](/images/math/9/7/9/97990582a2b53b495de72945c621e72f.png)
Theorem 3.2 [Barden1965]. The mapping
![\displaystyle \mathcal{M}_{5}(e) \rightarrow {\mathcal Ab}^{T \oplus T \oplus *} \times (\Nn \cup \{ \infty \}) , \quad [M] \mapsto ([H_2(M)], h(M))](/images/math/4/8/5/4855c33282a2801dab46d98157d124ae.png)
is an injection onto the subset of pairs ![([G], n)](/images/math/0/6/6/066c10d7231c9606db2b9be060eb18f6.png) where
where ![[G] \in {\mathcal Ab}^{T \oplus T \oplus \Zz_2}](/images/math/d/5/a/d5adb9bd1c6cad846bec22c61be697f0.png) if and only if
if and only if 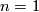 .
.
The above theorems follow from the following theorem of Barden and the classification of anti-symmetric linking forms.
Theorem 3.3 [Barden1965, Theorem 2.2]. Let  and
and  be simply-connected, closed, smooth 5-manifolds and let
be simply-connected, closed, smooth 5-manifolds and let 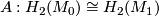 be an isomorphism preserving the linking form and the second Stiefel-Whitney class. Then
be an isomorphism preserving the linking form and the second Stiefel-Whitney class. Then  is realised by a diffeomorphism.
is realised by a diffeomorphism.
This theorem can re-phrased in categorical language as follows: let 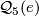 be a small category, in fact groupoid, with objects
be a small category, in fact groupoid, with objects 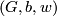 where
where  is a finitely generated abelian group,
is a finitely generated abelian group, 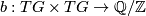 is a anti-symmetric non-singular linking form and
is a anti-symmetric non-singular linking form and 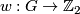 is a homomorphism such that
is a homomorphism such that 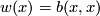 for all
for all 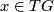 . The morphisms of
. The morphisms of 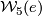 are isomorphisms of abelian groups commuting with both
are isomorphisms of abelian groups commuting with both  and
and  .
.
Now let 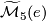 be a small category, actually groupoid, with objects simply-connected, closed, smooth 5-manifolds and morphisms isotopy diffeomorphisms. Let
be a small category, actually groupoid, with objects simply-connected, closed, smooth 5-manifolds and morphisms isotopy diffeomorphisms. Let 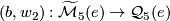 be the funtor which maps
be the funtor which maps  to
to 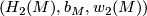 and
and 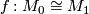 to the induced map on
to the induced map on 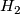 .
.
Theorem [Barden1965] 3.4. The functor
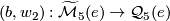
is a detecting functor. That is, it is surjective on objects and 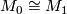 if and only if
if and only if 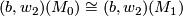 .
.
3.1 Enumeration
We give Barden's enumeration of the set 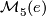 , [Barden1965, Theorem 2.3].
, [Barden1965, Theorem 2.3].
-
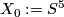 ,
, 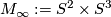 ,
, 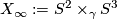 ,
, 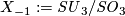 .
.
- For
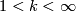 ,
, 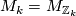 is the Spin manifold with
is the Spin manifold with 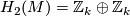 constructed above.
constructed above.
- For
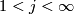 let
let 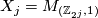 constructed above be the non-Spin manifold with
constructed above be the non-Spin manifold with 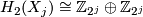 .
.
With this notation [Barden1965, Theorem 2.3] states that a complete list of diffeomorphism classes of simply-connected 5-manifolds is given by
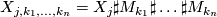
where 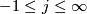 ,
, 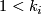 ,
, 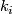 divides
divides 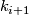 or
or 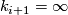 and
and  denotes the connected sum of oriented manifolds. The manifold
denotes the connected sum of oriented manifolds. The manifold 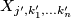 is diffeomorphic to
is diffeomorphic to 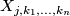 if and only if
if and only if 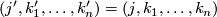 .
.
An alternative complete enumeration is obtained by writing 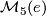 as a disjoint union
as a disjoint union
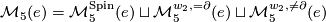
![\displaystyle \mathcal{M}_5^{\Spin}(e) = \{ [M_G] \}, ~~\mathcal{M}_5^{w_2, = \partial}(e) = \{ [M_{(G, \omega)}] \} ~~\text{and}~~ \mathcal{M}_5^{w_2, \neq \partial}(e) = \{ [ X_{-1} \sharp M_G] \}.](/images/math/7/d/b/7db70491f84c955347708c8b9f01004f.png)
4 Further discussion
- As the invariants which classify closed, oriented 5-manifolds are homotopy invariants, we see that the same classification holds up to homotopy, homeomorphism and piecewise linear homeomorphism.
- The classification of simply-connected Spin 5-manifolds was one of the first applications of the h-cobordism theorem.
- By the construction above every simply-connected, closed, smooth, Spin 5-manifold embedds into
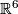 .
.
- As the invariants for
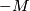 are isomorphic to the invariants of
are isomorphic to the invariants of  we see that every smooth 5-manifold admits an orientation reversing diffeomorphism: i.e. all 5-manifolds are smoothly amphicheiral.
we see that every smooth 5-manifold admits an orientation reversing diffeomorphism: i.e. all 5-manifolds are smoothly amphicheiral.
4.1 Bordism groups
As ![\mathcal{M}_5^{\Spin}(e) = \{[M_G]\}](/images/math/f/b/7/fb7063131a17d2e0dd1e2500231179b6.png) and
and 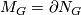 we see that every closed, Spin 5-manifold bounds a Spin 6-manifold. Hence the bordism group
we see that every closed, Spin 5-manifold bounds a Spin 6-manifold. Hence the bordism group 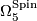 vanishes.
vanishes.
The bordism group 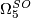 is isomorphic to
is isomorphic to  and is detected by the Stiefel-Whitney number
and is detected by the Stiefel-Whitney number ![\langle w_2(M)w_3(M), [M] \rangle \in \Zz_2](/images/math/9/b/9/9b9476a5ddc2349bc6380f1e03304d99.png) . The Wu-manifold has cohomology groups
. The Wu-manifold has cohomology groups
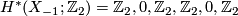
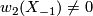 . It follows that
. It follows that 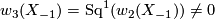 and that
and that ![\langle w_2(X_{-1})w_3(X_{-1}), [X_{-1}] \rangle \neq 0](/images/math/8/2/1/821189f95965b9293938b9750b268abc.png) . We see that
. We see that ![[X_{-1}]](/images/math/3/f/3/3f3bed6681734999df212ea7e3e6b26d.png) is the generator of
is the generator of 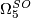 and that a closed, smooth 5-manifold
and that a closed, smooth 5-manifold  is not a boundary if and only if it is diffeomorphic to
is not a boundary if and only if it is diffeomorphic to 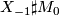 where
where  is a Spin manifold.
is a Spin manifold.
- !!! Add references here.
4.2 Curvature and contact structures
- Every manifold
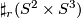 admits a metric of positive Ricci curvature [Boyer&Galicki2006].
admits a metric of positive Ricci curvature [Boyer&Galicki2006].
- Every Spin 5-manifold with the order of
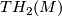 prime to 3 admits a contact structure [Thomas1986].
prime to 3 admits a contact structure [Thomas1986].
4.3 Mapping class groups
Let 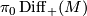 denote the group of isotopy classes of orientation preserving diffeomorphisms
denote the group of isotopy classes of orientation preserving diffeomorphisms 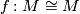 and let
and let 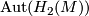 be the group of isomorphisms of
be the group of isomorphisms of 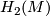 preserving the linking form and the second Stiefel-Whitney class. Applying the second statement of Barden's classification above
we obtain an exact sequence
preserving the linking form and the second Stiefel-Whitney class. Applying the second statement of Barden's classification above
we obtain an exact sequence
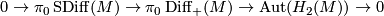
where 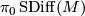 is the group of isotopy classes of diffeomorphisms inducing the identity on
is the group of isotopy classes of diffeomorphisms inducing the identity on 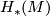 .
.
- Open problem: as of writing there is no computation of
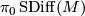 for a general simply-connected 5-manifold.
for a general simply-connected 5-manifold.
- The isotopy group
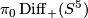 is known to be the trivial group [[[#|]]].
is known to be the trivial group [[[#|]]].
- In the homotopy category,
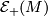 , the group of homotopy classes of orientation preserving homotopy equivalences of
, the group of homotopy classes of orientation preserving homotopy equivalences of  , has been extensively investigated by [Baues&Buth1996] and is already seen to be relatively complex.
, has been extensively investigated by [Baues&Buth1996] and is already seen to be relatively complex.
5 References
- [Baues&Buth1996] H. J. Baues and J. Buth, On the group of homotopy equivalences of simply connected five manifolds, Math. Z. 222 (1996), no.4, 573–614. MR1406269 (97g:55009) Zbl 0881.55008
- [Barden1965] D. Barden, Simply connected five-manifolds, Ann. of Math. (2) 82 (1965), 365–385. MR0184241 (32 #1714) Zbl 0136.20602
- [Boyer&Galicki2006] C. P. Boyer and K. Galicki, Highly connected manifolds with positive Ricci curvature, Geom. Topol. 10 (2006), 2219–2235 (electronic). MR2284055 (2007k:53057) Zbl 1129.53026
- [Smale1962] S. Smale, On the structure of
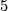 -manifolds, Ann. of Math. (2) 75 (1962), 38–46. MR0141133 (25 #4544) Zbl 0101.16103
-manifolds, Ann. of Math. (2) 75 (1962), 38–46. MR0141133 (25 #4544) Zbl 0101.16103
- [Thomas1986] C. B. Thomas, Contact structures on
 -connected
-connected 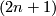 -manifolds, 18 (1986), 255–270. MR925869 (89b:53074) Zbl 0642.57014
-manifolds, 18 (1986), 255–270. MR925869 (89b:53074) Zbl 0642.57014
- [Wall1962] C. T. C. Wall, Killing the middle homotopy groups of odd dimensional manifolds, Trans. Amer. Math. Soc. 103 (1962), 421–433. MR0139185 (25 #2621) Zbl 0199.26803
- [Wall1963] C. T. C. Wall, Quadratic forms on finite groups, and related topics, Topology 2 (1963), 281–298. MR0156890 (28 #133) Zbl 0215.39903MediaWiki:Stub
 and let
and let 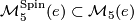 be the subset of diffeomorphism classes of spinable manifolds. In this article we report the calculation of
be the subset of diffeomorphism classes of spinable manifolds. In this article we report the calculation of 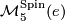 first obtained in [Smale1962] and of
first obtained in [Smale1962] and of 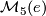 first obtained in general in [Barden1965].
first obtained in general in [Barden1965].
Contents |
1 Constructions and examples
We first list some familiar 5-manifolds using Barden's notation:
-
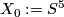
-
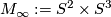
-
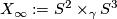 , the total space of the non-trivial
, the total space of the non-trivial  -bundle over
-bundle over 
-
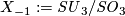 , the Wu-manifold, is the homogeneous space obtained from the standadard inclusion of
, the Wu-manifold, is the homogeneous space obtained from the standadard inclusion of 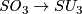 .
.
Next we present a construction of Spin 5-manifolds. Note that all homology groups are with integer coefficients. Given a finitely generated abelian group  , let
, let 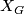 denote the degree 2 Moore space with
denote the degree 2 Moore space with 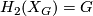 . The space
. The space 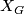 may be realised as a finite CW-complex and so there is an embedding
may be realised as a finite CW-complex and so there is an embedding 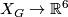 . Let
. Let 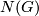 be a regular neighbourhood of
be a regular neighbourhood of 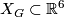 and let
and let 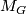 be the boundary of
be the boundary of 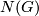 . Then
. Then 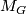 is a closed, smooth, simply-connected, spinable 5-manifold with
is a closed, smooth, simply-connected, spinable 5-manifold with  where
where 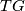 is the torsion subgroup of
is the torsion subgroup of  . For example,
. For example, 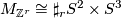 where
where 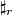 denotes the
denotes the  -fold connected sum.
-fold connected sum.
For the non-Spin case let 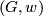 be a pair with
be a pair with 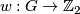 a surjective homomorphism and
a surjective homomorphism and  as above. We shall construct a non-Spin 5-manifold
as above. We shall construct a non-Spin 5-manifold 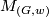 with
with 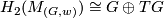 and second Stiefel-Whitney class
and second Stiefel-Whitney class 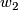 given by
given by  composed with the projection
composed with the projection 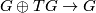 . If
. If 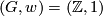 let
let 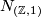 be the non-trivial
be the non-trivial 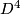 -bundle over
-bundle over  with boundary
with boundary 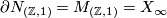 . If
. If 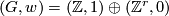 let
let 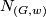 be the boundary connected sum
be the boundary connected sum 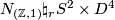 with boundary
with boundary 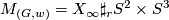 . In the general case, present
. In the general case, present 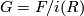 where
where 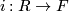 is an injective homomorphism between free abelian groups. Lift
is an injective homomorphism between free abelian groups. Lift 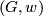 to
to 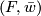 and observe that there is a canonical identification
and observe that there is a canonical identification 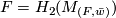 . If
. If 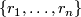 is a basis for
is a basis for  note that each
note that each 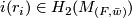 is represented by a an embedded 2-sphere with trivial normal bundle. Let
is represented by a an embedded 2-sphere with trivial normal bundle. Let 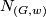 be the manifold obtained by attaching 3-handles to
be the manifold obtained by attaching 3-handles to 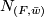 along spheres representing
along spheres representing 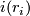 and let
and let 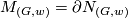 . One may check that
. One may check that 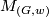 is a non-Spin manifold as described above.
is a non-Spin manifold as described above.
- !!! To do: determine which 1-connected 5-manifolds appear as Brieskorn varieties.
2 Invariants
Consider the following invariants of a closed simply-connected 5-manifold  .
.
-
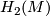 be the second integral homology group of
be the second integral homology group of  , with torsion subgroup
, with torsion subgroup 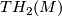 .
.
-
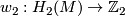 , the homomorphism defined by evaluation with the second Stiefel-Whitney class of
, the homomorphism defined by evaluation with the second Stiefel-Whitney class of  ,
, 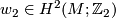 .
.
-
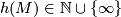 , the smallest extended natural number
, the smallest extended natural number  such that
such that 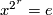 and
and 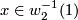 . If
. If  is Spin we set
is Spin we set 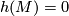 .
.
-
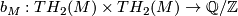 , the linking form of
, the linking form of  which is a non-singular anti-symmetric bi-linear pairing on
which is a non-singular anti-symmetric bi-linear pairing on 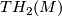 .
.
By [Wall1962, Proposition 1 & 2] the linking form satisfies the identity 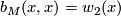 where we regard
where we regard 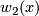 as an element of
as an element of 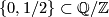 .
.
For example, the Wu-manifold 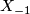 has
has 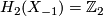 , non-trivial
, non-trivial 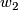 and
and 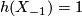 .
.
An abstract non-singular, anti-symmetric linking form 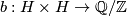 on a finite group
on a finite group  is a bi-linear function such that
is a bi-linear function such that 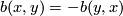 and
and 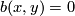 for all
for all 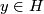 if and only if
if and only if 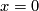 . By [Wall1963] such linking forms are classified up to isomorphism by the homomorphism
. By [Wall1963] such linking forms are classified up to isomorphism by the homomorphism 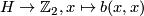 . Moreover
. Moreover  must be isomorphic to
must be isomorphic to 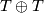 or
or 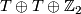 for some finite group
for some finite group  with
with 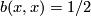 if
if  generates the
generates the  summand. In particular the second Stiefel-Whitney class of a 5-manifold
summand. In particular the second Stiefel-Whitney class of a 5-manifold  determines the isomorphism class of the linking form
determines the isomorphism class of the linking form 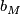 and we see that the torsion subgroup of
and we see that the torsion subgroup of 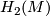 is of the form
is of the form 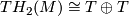 if
if 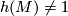 or
or 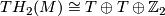 if
if 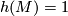 in which case the
in which case the  summand is an orthogonal summand of
summand is an orthogonal summand of 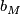 .
.
3 Classification
We first present the most economical classifications of  and
and 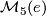 . Let
. Let 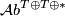 be the set of isomorphism classes finitely generated abelian groups
be the set of isomorphism classes finitely generated abelian groups  with torsion subgroup
with torsion subgroup 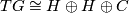 where
where  is trivial or
is trivial or 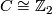 and write
and write 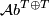 and
and 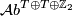 for the obvious subsets.
for the obvious subsets.
![\displaystyle \mathcal{M}_5^{\Spin}(e) \rightarrow {\mathcal Ab}^{T\oplus T}, \quad [M] \mapsto [H_2(M)].](/images/math/9/7/9/97990582a2b53b495de72945c621e72f.png)
Theorem 3.2 [Barden1965]. The mapping
![\displaystyle \mathcal{M}_{5}(e) \rightarrow {\mathcal Ab}^{T \oplus T \oplus *} \times (\Nn \cup \{ \infty \}) , \quad [M] \mapsto ([H_2(M)], h(M))](/images/math/4/8/5/4855c33282a2801dab46d98157d124ae.png)
is an injection onto the subset of pairs ![([G], n)](/images/math/0/6/6/066c10d7231c9606db2b9be060eb18f6.png) where
where ![[G] \in {\mathcal Ab}^{T \oplus T \oplus \Zz_2}](/images/math/d/5/a/d5adb9bd1c6cad846bec22c61be697f0.png) if and only if
if and only if 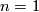 .
.
The above theorems follow from the following theorem of Barden and the classification of anti-symmetric linking forms.
Theorem 3.3 [Barden1965, Theorem 2.2]. Let  and
and  be simply-connected, closed, smooth 5-manifolds and let
be simply-connected, closed, smooth 5-manifolds and let 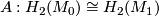 be an isomorphism preserving the linking form and the second Stiefel-Whitney class. Then
be an isomorphism preserving the linking form and the second Stiefel-Whitney class. Then  is realised by a diffeomorphism.
is realised by a diffeomorphism.
This theorem can re-phrased in categorical language as follows: let 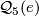 be a small category, in fact groupoid, with objects
be a small category, in fact groupoid, with objects 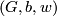 where
where  is a finitely generated abelian group,
is a finitely generated abelian group, 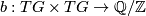 is a anti-symmetric non-singular linking form and
is a anti-symmetric non-singular linking form and 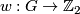 is a homomorphism such that
is a homomorphism such that 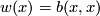 for all
for all 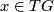 . The morphisms of
. The morphisms of 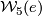 are isomorphisms of abelian groups commuting with both
are isomorphisms of abelian groups commuting with both  and
and  .
.
Now let 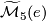 be a small category, actually groupoid, with objects simply-connected, closed, smooth 5-manifolds and morphisms isotopy diffeomorphisms. Let
be a small category, actually groupoid, with objects simply-connected, closed, smooth 5-manifolds and morphisms isotopy diffeomorphisms. Let 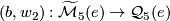 be the funtor which maps
be the funtor which maps  to
to 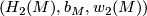 and
and 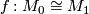 to the induced map on
to the induced map on 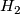 .
.
Theorem [Barden1965] 3.4. The functor
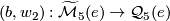
is a detecting functor. That is, it is surjective on objects and 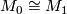 if and only if
if and only if 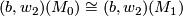 .
.
3.1 Enumeration
We give Barden's enumeration of the set 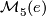 , [Barden1965, Theorem 2.3].
, [Barden1965, Theorem 2.3].
-
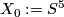 ,
, 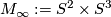 ,
, 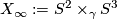 ,
, 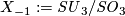 .
.
- For
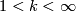 ,
, 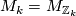 is the Spin manifold with
is the Spin manifold with 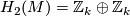 constructed above.
constructed above.
- For
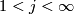 let
let 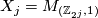 constructed above be the non-Spin manifold with
constructed above be the non-Spin manifold with 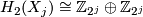 .
.
With this notation [Barden1965, Theorem 2.3] states that a complete list of diffeomorphism classes of simply-connected 5-manifolds is given by
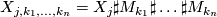
where 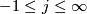 ,
, 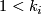 ,
, 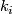 divides
divides 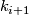 or
or 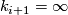 and
and  denotes the connected sum of oriented manifolds. The manifold
denotes the connected sum of oriented manifolds. The manifold 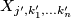 is diffeomorphic to
is diffeomorphic to 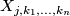 if and only if
if and only if 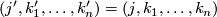 .
.
An alternative complete enumeration is obtained by writing 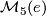 as a disjoint union
as a disjoint union
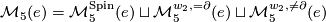
![\displaystyle \mathcal{M}_5^{\Spin}(e) = \{ [M_G] \}, ~~\mathcal{M}_5^{w_2, = \partial}(e) = \{ [M_{(G, \omega)}] \} ~~\text{and}~~ \mathcal{M}_5^{w_2, \neq \partial}(e) = \{ [ X_{-1} \sharp M_G] \}.](/images/math/7/d/b/7db70491f84c955347708c8b9f01004f.png)
4 Further discussion
- As the invariants which classify closed, oriented 5-manifolds are homotopy invariants, we see that the same classification holds up to homotopy, homeomorphism and piecewise linear homeomorphism.
- The classification of simply-connected Spin 5-manifolds was one of the first applications of the h-cobordism theorem.
- By the construction above every simply-connected, closed, smooth, Spin 5-manifold embedds into
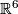 .
.
- As the invariants for
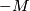 are isomorphic to the invariants of
are isomorphic to the invariants of  we see that every smooth 5-manifold admits an orientation reversing diffeomorphism: i.e. all 5-manifolds are smoothly amphicheiral.
we see that every smooth 5-manifold admits an orientation reversing diffeomorphism: i.e. all 5-manifolds are smoothly amphicheiral.
4.1 Bordism groups
As ![\mathcal{M}_5^{\Spin}(e) = \{[M_G]\}](/images/math/f/b/7/fb7063131a17d2e0dd1e2500231179b6.png) and
and 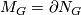 we see that every closed, Spin 5-manifold bounds a Spin 6-manifold. Hence the bordism group
we see that every closed, Spin 5-manifold bounds a Spin 6-manifold. Hence the bordism group 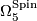 vanishes.
vanishes.
The bordism group 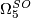 is isomorphic to
is isomorphic to  and is detected by the Stiefel-Whitney number
and is detected by the Stiefel-Whitney number ![\langle w_2(M)w_3(M), [M] \rangle \in \Zz_2](/images/math/9/b/9/9b9476a5ddc2349bc6380f1e03304d99.png) . The Wu-manifold has cohomology groups
. The Wu-manifold has cohomology groups
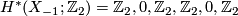
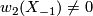 . It follows that
. It follows that 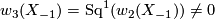 and that
and that ![\langle w_2(X_{-1})w_3(X_{-1}), [X_{-1}] \rangle \neq 0](/images/math/8/2/1/821189f95965b9293938b9750b268abc.png) . We see that
. We see that ![[X_{-1}]](/images/math/3/f/3/3f3bed6681734999df212ea7e3e6b26d.png) is the generator of
is the generator of 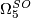 and that a closed, smooth 5-manifold
and that a closed, smooth 5-manifold  is not a boundary if and only if it is diffeomorphic to
is not a boundary if and only if it is diffeomorphic to 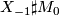 where
where  is a Spin manifold.
is a Spin manifold.
- !!! Add references here.
4.2 Curvature and contact structures
- Every manifold
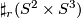 admits a metric of positive Ricci curvature [Boyer&Galicki2006].
admits a metric of positive Ricci curvature [Boyer&Galicki2006].
- Every Spin 5-manifold with the order of
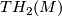 prime to 3 admits a contact structure [Thomas1986].
prime to 3 admits a contact structure [Thomas1986].
4.3 Mapping class groups
Let 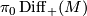 denote the group of isotopy classes of orientation preserving diffeomorphisms
denote the group of isotopy classes of orientation preserving diffeomorphisms 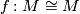 and let
and let 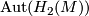 be the group of isomorphisms of
be the group of isomorphisms of 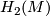 preserving the linking form and the second Stiefel-Whitney class. Applying the second statement of Barden's classification above
we obtain an exact sequence
preserving the linking form and the second Stiefel-Whitney class. Applying the second statement of Barden's classification above
we obtain an exact sequence
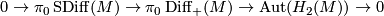
where 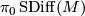 is the group of isotopy classes of diffeomorphisms inducing the identity on
is the group of isotopy classes of diffeomorphisms inducing the identity on 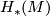 .
.
- Open problem: as of writing there is no computation of
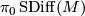 for a general simply-connected 5-manifold.
for a general simply-connected 5-manifold.
- The isotopy group
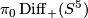 is known to be the trivial group [[[#|]]].
is known to be the trivial group [[[#|]]].
- In the homotopy category,
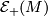 , the group of homotopy classes of orientation preserving homotopy equivalences of
, the group of homotopy classes of orientation preserving homotopy equivalences of  , has been extensively investigated by [Baues&Buth1996] and is already seen to be relatively complex.
, has been extensively investigated by [Baues&Buth1996] and is already seen to be relatively complex.
5 References
- [Baues&Buth1996] H. J. Baues and J. Buth, On the group of homotopy equivalences of simply connected five manifolds, Math. Z. 222 (1996), no.4, 573–614. MR1406269 (97g:55009) Zbl 0881.55008
- [Barden1965] D. Barden, Simply connected five-manifolds, Ann. of Math. (2) 82 (1965), 365–385. MR0184241 (32 #1714) Zbl 0136.20602
- [Boyer&Galicki2006] C. P. Boyer and K. Galicki, Highly connected manifolds with positive Ricci curvature, Geom. Topol. 10 (2006), 2219–2235 (electronic). MR2284055 (2007k:53057) Zbl 1129.53026
- [Smale1962] S. Smale, On the structure of
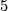 -manifolds, Ann. of Math. (2) 75 (1962), 38–46. MR0141133 (25 #4544) Zbl 0101.16103
-manifolds, Ann. of Math. (2) 75 (1962), 38–46. MR0141133 (25 #4544) Zbl 0101.16103
- [Thomas1986] C. B. Thomas, Contact structures on
 -connected
-connected 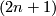 -manifolds, 18 (1986), 255–270. MR925869 (89b:53074) Zbl 0642.57014
-manifolds, 18 (1986), 255–270. MR925869 (89b:53074) Zbl 0642.57014
- [Wall1962] C. T. C. Wall, Killing the middle homotopy groups of odd dimensional manifolds, Trans. Amer. Math. Soc. 103 (1962), 421–433. MR0139185 (25 #2621) Zbl 0199.26803
- [Wall1963] C. T. C. Wall, Quadratic forms on finite groups, and related topics, Topology 2 (1963), 281–298. MR0156890 (28 #133) Zbl 0215.39903MediaWiki:Stub
 and let
and let 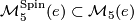 be the subset of diffeomorphism classes of spinable manifolds. In this article we report the calculation of
be the subset of diffeomorphism classes of spinable manifolds. In this article we report the calculation of 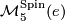 first obtained in [Smale1962] and of
first obtained in [Smale1962] and of 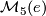 first obtained in general in [Barden1965].
first obtained in general in [Barden1965].
Contents |
1 Constructions and examples
We first list some familiar 5-manifolds using Barden's notation:
-
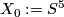
-
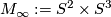
-
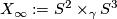 , the total space of the non-trivial
, the total space of the non-trivial  -bundle over
-bundle over 
-
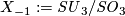 , the Wu-manifold, is the homogeneous space obtained from the standadard inclusion of
, the Wu-manifold, is the homogeneous space obtained from the standadard inclusion of 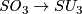 .
.
Next we present a construction of Spin 5-manifolds. Note that all homology groups are with integer coefficients. Given a finitely generated abelian group  , let
, let 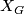 denote the degree 2 Moore space with
denote the degree 2 Moore space with 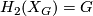 . The space
. The space 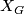 may be realised as a finite CW-complex and so there is an embedding
may be realised as a finite CW-complex and so there is an embedding 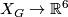 . Let
. Let 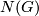 be a regular neighbourhood of
be a regular neighbourhood of 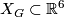 and let
and let 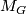 be the boundary of
be the boundary of 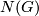 . Then
. Then 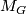 is a closed, smooth, simply-connected, spinable 5-manifold with
is a closed, smooth, simply-connected, spinable 5-manifold with  where
where 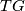 is the torsion subgroup of
is the torsion subgroup of  . For example,
. For example, 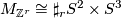 where
where 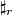 denotes the
denotes the  -fold connected sum.
-fold connected sum.
For the non-Spin case let 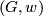 be a pair with
be a pair with 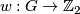 a surjective homomorphism and
a surjective homomorphism and  as above. We shall construct a non-Spin 5-manifold
as above. We shall construct a non-Spin 5-manifold 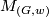 with
with 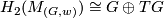 and second Stiefel-Whitney class
and second Stiefel-Whitney class 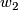 given by
given by  composed with the projection
composed with the projection 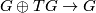 . If
. If 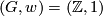 let
let 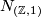 be the non-trivial
be the non-trivial 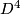 -bundle over
-bundle over  with boundary
with boundary 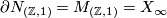 . If
. If 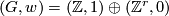 let
let 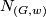 be the boundary connected sum
be the boundary connected sum 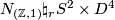 with boundary
with boundary 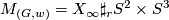 . In the general case, present
. In the general case, present 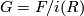 where
where 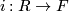 is an injective homomorphism between free abelian groups. Lift
is an injective homomorphism between free abelian groups. Lift 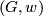 to
to 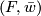 and observe that there is a canonical identification
and observe that there is a canonical identification 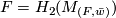 . If
. If 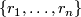 is a basis for
is a basis for  note that each
note that each 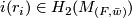 is represented by a an embedded 2-sphere with trivial normal bundle. Let
is represented by a an embedded 2-sphere with trivial normal bundle. Let 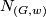 be the manifold obtained by attaching 3-handles to
be the manifold obtained by attaching 3-handles to 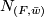 along spheres representing
along spheres representing 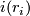 and let
and let 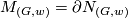 . One may check that
. One may check that 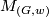 is a non-Spin manifold as described above.
is a non-Spin manifold as described above.
- !!! To do: determine which 1-connected 5-manifolds appear as Brieskorn varieties.
2 Invariants
Consider the following invariants of a closed simply-connected 5-manifold  .
.
-
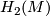 be the second integral homology group of
be the second integral homology group of  , with torsion subgroup
, with torsion subgroup 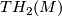 .
.
-
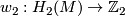 , the homomorphism defined by evaluation with the second Stiefel-Whitney class of
, the homomorphism defined by evaluation with the second Stiefel-Whitney class of  ,
, 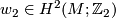 .
.
-
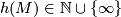 , the smallest extended natural number
, the smallest extended natural number  such that
such that 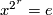 and
and 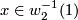 . If
. If  is Spin we set
is Spin we set 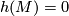 .
.
-
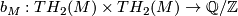 , the linking form of
, the linking form of  which is a non-singular anti-symmetric bi-linear pairing on
which is a non-singular anti-symmetric bi-linear pairing on 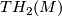 .
.
By [Wall1962, Proposition 1 & 2] the linking form satisfies the identity 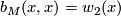 where we regard
where we regard 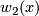 as an element of
as an element of  .
.
For example, the Wu-manifold 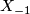 has
has 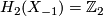 , non-trivial
, non-trivial 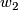 and
and 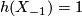 .
.
An abstract non-singular, anti-symmetric linking form 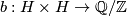 on a finite group
on a finite group  is a bi-linear function such that
is a bi-linear function such that 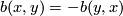 and
and 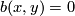 for all
for all 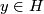 if and only if
if and only if 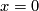 . By [Wall1963] such linking forms are classified up to isomorphism by the homomorphism
. By [Wall1963] such linking forms are classified up to isomorphism by the homomorphism 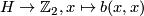 . Moreover
. Moreover  must be isomorphic to
must be isomorphic to 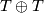 or
or 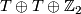 for some finite group
for some finite group  with
with 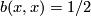 if
if  generates the
generates the  summand. In particular the second Stiefel-Whitney class of a 5-manifold
summand. In particular the second Stiefel-Whitney class of a 5-manifold  determines the isomorphism class of the linking form
determines the isomorphism class of the linking form 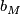 and we see that the torsion subgroup of
and we see that the torsion subgroup of 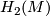 is of the form
is of the form 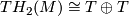 if
if 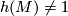 or
or 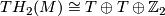 if
if 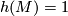 in which case the
in which case the  summand is an orthogonal summand of
summand is an orthogonal summand of 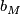 .
.
3 Classification
We first present the most economical classifications of  and
and 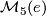 . Let
. Let 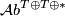 be the set of isomorphism classes finitely generated abelian groups
be the set of isomorphism classes finitely generated abelian groups  with torsion subgroup
with torsion subgroup 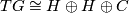 where
where  is trivial or
is trivial or 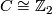 and write
and write 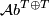 and
and 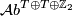 for the obvious subsets.
for the obvious subsets.
![\displaystyle \mathcal{M}_5^{\Spin}(e) \rightarrow {\mathcal Ab}^{T\oplus T}, \quad [M] \mapsto [H_2(M)].](/images/math/9/7/9/97990582a2b53b495de72945c621e72f.png)
Theorem 3.2 [Barden1965]. The mapping
![\displaystyle \mathcal{M}_{5}(e) \rightarrow {\mathcal Ab}^{T \oplus T \oplus *} \times (\Nn \cup \{ \infty \}) , \quad [M] \mapsto ([H_2(M)], h(M))](/images/math/4/8/5/4855c33282a2801dab46d98157d124ae.png)
is an injection onto the subset of pairs ![([G], n)](/images/math/0/6/6/066c10d7231c9606db2b9be060eb18f6.png) where
where ![[G] \in {\mathcal Ab}^{T \oplus T \oplus \Zz_2}](/images/math/d/5/a/d5adb9bd1c6cad846bec22c61be697f0.png) if and only if
if and only if 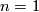 .
.
The above theorems follow from the following theorem of Barden and the classification of anti-symmetric linking forms.
Theorem 3.3 [Barden1965, Theorem 2.2]. Let  and
and  be simply-connected, closed, smooth 5-manifolds and let
be simply-connected, closed, smooth 5-manifolds and let 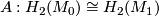 be an isomorphism preserving the linking form and the second Stiefel-Whitney class. Then
be an isomorphism preserving the linking form and the second Stiefel-Whitney class. Then  is realised by a diffeomorphism.
is realised by a diffeomorphism.
This theorem can re-phrased in categorical language as follows: let 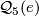 be a small category, in fact groupoid, with objects
be a small category, in fact groupoid, with objects 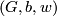 where
where  is a finitely generated abelian group,
is a finitely generated abelian group, 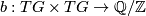 is a anti-symmetric non-singular linking form and
is a anti-symmetric non-singular linking form and 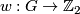 is a homomorphism such that
is a homomorphism such that 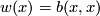 for all
for all 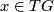 . The morphisms of
. The morphisms of 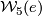 are isomorphisms of abelian groups commuting with both
are isomorphisms of abelian groups commuting with both  and
and  .
.
Now let 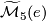 be a small category, actually groupoid, with objects simply-connected, closed, smooth 5-manifolds and morphisms isotopy diffeomorphisms. Let
be a small category, actually groupoid, with objects simply-connected, closed, smooth 5-manifolds and morphisms isotopy diffeomorphisms. Let 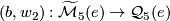 be the funtor which maps
be the funtor which maps  to
to 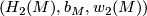 and
and 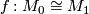 to the induced map on
to the induced map on 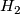 .
.
Theorem [Barden1965] 3.4. The functor
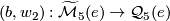
is a detecting functor. That is, it is surjective on objects and 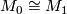 if and only if
if and only if 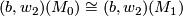 .
.
3.1 Enumeration
We give Barden's enumeration of the set 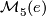 , [Barden1965, Theorem 2.3].
, [Barden1965, Theorem 2.3].
-
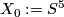 ,
, 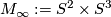 ,
, 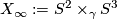 ,
, 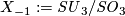 .
.
- For
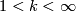 ,
, 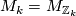 is the Spin manifold with
is the Spin manifold with 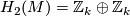 constructed above.
constructed above.
- For
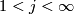 let
let 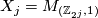 constructed above be the non-Spin manifold with
constructed above be the non-Spin manifold with 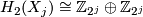 .
.
With this notation [Barden1965, Theorem 2.3] states that a complete list of diffeomorphism classes of simply-connected 5-manifolds is given by
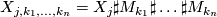
where 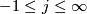 ,
, 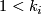 ,
, 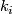 divides
divides 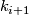 or
or 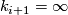 and
and  denotes the connected sum of oriented manifolds. The manifold
denotes the connected sum of oriented manifolds. The manifold 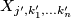 is diffeomorphic to
is diffeomorphic to 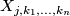 if and only if
if and only if 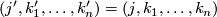 .
.
An alternative complete enumeration is obtained by writing 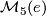 as a disjoint union
as a disjoint union
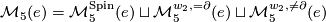
![\displaystyle \mathcal{M}_5^{\Spin}(e) = \{ [M_G] \}, ~~\mathcal{M}_5^{w_2, = \partial}(e) = \{ [M_{(G, \omega)}] \} ~~\text{and}~~ \mathcal{M}_5^{w_2, \neq \partial}(e) = \{ [ X_{-1} \sharp M_G] \}.](/images/math/7/d/b/7db70491f84c955347708c8b9f01004f.png)
4 Further discussion
- As the invariants which classify closed, oriented 5-manifolds are homotopy invariants, we see that the same classification holds up to homotopy, homeomorphism and piecewise linear homeomorphism.
- The classification of simply-connected Spin 5-manifolds was one of the first applications of the h-cobordism theorem.
- By the construction above every simply-connected, closed, smooth, Spin 5-manifold embedds into
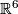 .
.
- As the invariants for
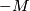 are isomorphic to the invariants of
are isomorphic to the invariants of  we see that every smooth 5-manifold admits an orientation reversing diffeomorphism: i.e. all 5-manifolds are smoothly amphicheiral.
we see that every smooth 5-manifold admits an orientation reversing diffeomorphism: i.e. all 5-manifolds are smoothly amphicheiral.
4.1 Bordism groups
As ![\mathcal{M}_5^{\Spin}(e) = \{[M_G]\}](/images/math/f/b/7/fb7063131a17d2e0dd1e2500231179b6.png) and
and 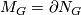 we see that every closed, Spin 5-manifold bounds a Spin 6-manifold. Hence the bordism group
we see that every closed, Spin 5-manifold bounds a Spin 6-manifold. Hence the bordism group 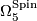 vanishes.
vanishes.
The bordism group 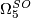 is isomorphic to
is isomorphic to  and is detected by the Stiefel-Whitney number
and is detected by the Stiefel-Whitney number ![\langle w_2(M)w_3(M), [M] \rangle \in \Zz_2](/images/math/9/b/9/9b9476a5ddc2349bc6380f1e03304d99.png) . The Wu-manifold has cohomology groups
. The Wu-manifold has cohomology groups
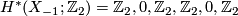
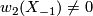 . It follows that
. It follows that 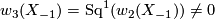 and that
and that ![\langle w_2(X_{-1})w_3(X_{-1}), [X_{-1}] \rangle \neq 0](/images/math/8/2/1/821189f95965b9293938b9750b268abc.png) . We see that
. We see that ![[X_{-1}]](/images/math/3/f/3/3f3bed6681734999df212ea7e3e6b26d.png) is the generator of
is the generator of 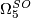 and that a closed, smooth 5-manifold
and that a closed, smooth 5-manifold  is not a boundary if and only if it is diffeomorphic to
is not a boundary if and only if it is diffeomorphic to 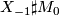 where
where  is a Spin manifold.
is a Spin manifold.
- !!! Add references here.
4.2 Curvature and contact structures
- Every manifold
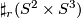 admits a metric of positive Ricci curvature [Boyer&Galicki2006].
admits a metric of positive Ricci curvature [Boyer&Galicki2006].
- Every Spin 5-manifold with the order of
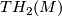 prime to 3 admits a contact structure [Thomas1986].
prime to 3 admits a contact structure [Thomas1986].
4.3 Mapping class groups
Let 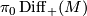 denote the group of isotopy classes of orientation preserving diffeomorphisms
denote the group of isotopy classes of orientation preserving diffeomorphisms 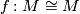 and let
and let 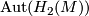 be the group of isomorphisms of
be the group of isomorphisms of 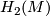 preserving the linking form and the second Stiefel-Whitney class. Applying the second statement of Barden's classification above
we obtain an exact sequence
preserving the linking form and the second Stiefel-Whitney class. Applying the second statement of Barden's classification above
we obtain an exact sequence
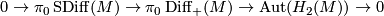
where 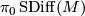 is the group of isotopy classes of diffeomorphisms inducing the identity on
is the group of isotopy classes of diffeomorphisms inducing the identity on 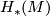 .
.
- Open problem: as of writing there is no computation of
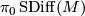 for a general simply-connected 5-manifold.
for a general simply-connected 5-manifold.
- The isotopy group
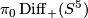 is known to be the trivial group [[[#|]]].
is known to be the trivial group [[[#|]]].
- In the homotopy category,
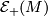 , the group of homotopy classes of orientation preserving homotopy equivalences of
, the group of homotopy classes of orientation preserving homotopy equivalences of  , has been extensively investigated by [Baues&Buth1996] and is already seen to be relatively complex.
, has been extensively investigated by [Baues&Buth1996] and is already seen to be relatively complex.
5 References
- [Baues&Buth1996] H. J. Baues and J. Buth, On the group of homotopy equivalences of simply connected five manifolds, Math. Z. 222 (1996), no.4, 573–614. MR1406269 (97g:55009) Zbl 0881.55008
- [Barden1965] D. Barden, Simply connected five-manifolds, Ann. of Math. (2) 82 (1965), 365–385. MR0184241 (32 #1714) Zbl 0136.20602
- [Boyer&Galicki2006] C. P. Boyer and K. Galicki, Highly connected manifolds with positive Ricci curvature, Geom. Topol. 10 (2006), 2219–2235 (electronic). MR2284055 (2007k:53057) Zbl 1129.53026
- [Smale1962] S. Smale, On the structure of
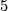 -manifolds, Ann. of Math. (2) 75 (1962), 38–46. MR0141133 (25 #4544) Zbl 0101.16103
-manifolds, Ann. of Math. (2) 75 (1962), 38–46. MR0141133 (25 #4544) Zbl 0101.16103
- [Thomas1986] C. B. Thomas, Contact structures on
 -connected
-connected 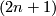 -manifolds, 18 (1986), 255–270. MR925869 (89b:53074) Zbl 0642.57014
-manifolds, 18 (1986), 255–270. MR925869 (89b:53074) Zbl 0642.57014
- [Wall1962] C. T. C. Wall, Killing the middle homotopy groups of odd dimensional manifolds, Trans. Amer. Math. Soc. 103 (1962), 421–433. MR0139185 (25 #2621) Zbl 0199.26803
- [Wall1963] C. T. C. Wall, Quadratic forms on finite groups, and related topics, Topology 2 (1963), 281–298. MR0156890 (28 #133) Zbl 0215.39903MediaWiki:Stub