Π-trivial map
(Difference between revisions)
m (Change to emphasise that a choice of lift is required for a Pi-trivial map to represent homology in the cover and that this lift should be part of the data in being a Pi-trivial map) |
|||
| Line 2: | Line 2: | ||
== Introduction == | == Introduction == | ||
<wikitex>; | <wikitex>; | ||
| − | This page is based on \cite{Ranicki2002}. A map $f:N^n\to M^m$ between manifolds represents a homology class $f_*[N] \in H_n(M)$. Let $(\widetilde{M},\pi,w)$ be an [[Oriented Cover|oriented cover]] with covering map $p:\widetilde{M} \to M$. If $f$ factors through $\widetilde{M}$ as $f= p\circ \widetilde{f}: N \to \widetilde{M}\to M$ then $f$ represents a homology class $\widetilde{f}_*[N]\in H_n(\widetilde{M})$. | + | This page is based on \cite{Ranicki2002}. A map $f:N^n\to M^m$ between manifolds represents a homology class $f_*[N] \in H_n(M)$. Let $(\widetilde{M},\pi,w)$ be an [[Oriented Cover|oriented cover]] with covering map $p:\widetilde{M} \to M$. If $f$ factors through $\widetilde{M}$ as $f= p\circ \widetilde{f}: N \to \widetilde{M}\to M$ then $f$ represents a homology class $\widetilde{f}_*[N]\in H_n(\widetilde{M})$. Note that a '''choice''' of lift $\widetilde{f}$ is required in order to represent a homology class. |
By covering space theory (c.f. \cite{Hatcher2002|Proposition 1.33}) a map $f:N\to M$ can be lifted to $\widetilde{M}$ if and only if $f_*(\pi_1(N)) \subset p_*(\pi_1(\widetilde{M}))$, i.e. if and only if the composition $q\circ f_*:\pi_1(N)\to \pi_1(M) \to \pi$ is trivial for $q:\pi_1(M)\to \pi_1(M)/\pi_1(\widetilde{M}) = \pi$ the quotient map. | By covering space theory (c.f. \cite{Hatcher2002|Proposition 1.33}) a map $f:N\to M$ can be lifted to $\widetilde{M}$ if and only if $f_*(\pi_1(N)) \subset p_*(\pi_1(\widetilde{M}))$, i.e. if and only if the composition $q\circ f_*:\pi_1(N)\to \pi_1(M) \to \pi$ is trivial for $q:\pi_1(M)\to \pi_1(M)/\pi_1(\widetilde{M}) = \pi$ the quotient map. | ||
| Line 9: | Line 9: | ||
== Definition == | == Definition == | ||
<wikitex>; | <wikitex>; | ||
| − | Let $M$ be an $m$-dimensional manifold and let $(\widetilde{M},\pi,w)$ be an [[Oriented Cover|oriented cover]]. A '''$\pi$-trivial map''' $f:N^n\to M^m$ is a map from an oriented manifold $N$ such that the composite | + | Let $M$ be an $m$-dimensional manifold and let $(\widetilde{M},\pi,w)$ be an [[Oriented Cover|oriented cover]]. A '''$\pi$-trivial map''' $f:N^n\to M^m$ is a map from an oriented manifold $N$, together with a choice of lift $\widetilde{f}:N \to \widetilde{M}$, such that the composite |
$$\xymatrix{ | $$\xymatrix{ | ||
\pi_1(N) \ar[r]^-{f_*} & \pi_1(M) \ar[r] & \pi | \pi_1(N) \ar[r]^-{f_*} & \pi_1(M) \ar[r] & \pi | ||
Revision as of 12:51, 19 April 2013
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
This page is based on [Ranicki2002]. A map 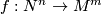 between manifolds represents a homology class
between manifolds represents a homology class ![f_*[N] \in H_n(M)](/images/math/3/d/2/3d21d4bf00b5770f8382bf0d70aa035e.png) . Let
. Let 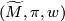 be an oriented cover with covering map
be an oriented cover with covering map 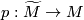 . If
. If  factors through
factors through  as
as 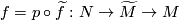 then
then  represents a homology class
represents a homology class ![\widetilde{f}_*[N]\in H_n(\widetilde{M})](/images/math/c/a/a/caa1901615f9a1811d1f344376d0e5a2.png) . Note that a choice of lift
. Note that a choice of lift 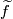 is required in order to represent a homology class.
is required in order to represent a homology class.
By covering space theory (c.f. [Hatcher2002, Proposition 1.33]) a map 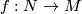 can be lifted to
can be lifted to  if and only if
if and only if 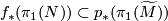 , i.e. if and only if the composition
, i.e. if and only if the composition 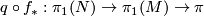 is trivial for
is trivial for 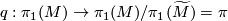 the quotient map.
the quotient map.
2 Definition
Let  be an
be an  -dimensional manifold and let
-dimensional manifold and let 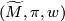 be an oriented cover. A
be an oriented cover. A  -trivial map
-trivial map 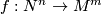 is a map from an oriented manifold
is a map from an oriented manifold  , together with a choice of lift
, together with a choice of lift 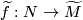 , such that the composite
, such that the composite
![\displaystyle \xymatrix{ \pi_1(N) \ar[r]^-{f_*} & \pi_1(M) \ar[r] & \pi }](/images/math/a/f/6/af62534d631fe62ab4fd71ba1af6a259.png)
is trivial.
3 Properties
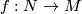 that factors through
that factors through  must map all of
must map all of  to the same sheet of
to the same sheet of  , hence the pullback satisfies
, hence the pullback satisfies 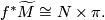
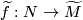 , which thought of as a map from
, which thought of as a map from 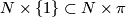 extends equivariantly to a lift
extends equivariantly to a lift 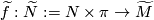 .
.
4 Examples
...
5 References
- [Hatcher2002] A. Hatcher, Algebraic topology, Cambridge University Press, 2002. MR1867354 (2002k:55001) Zbl 1044.55001
- [Ranicki2002] A. Ranicki, Algebraic and geometric surgery, The Clarendon Press Oxford University Press, Oxford, 2002. MR2061749 (2005e:57075) Zbl 1003.57001