Talk:Normal bordism - definitions (Ex)
From Manifold Atlas
Revision as of 10:06, 2 April 2012 by Andreas Hermann (Talk | contribs)
Part 1
Let  be a connected finite Poincare complex of dimension
be a connected finite Poincare complex of dimension  and let
and let 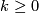 .
We define
.
We define
![\displaystyle \mathcal{N}_n(X,k):= \left\{ [\xi,M,i,f,\overline{f}] | \begin{array}{l} \xi\textrm{ vector bundle of rank }k\textrm{ over }X,\, M\textrm{ closed manifold of dimension }n,\, i:\,M\to\mathbb{R}^{n+k}\textrm{ embedding},\, (f,\overline{f}):\,\nu(M,i)\to\xi\textrm{ bundle map},\, f\textrm{ of degree }1 \end{array} \right\}](/images/math/3/8/9/38962ae773ef41b834b8be2c52e0655e.png)
where we identify 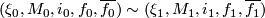 iff
iff
1) there exists  compact manifold of dimension
compact manifold of dimension 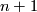 such that
such that 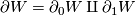
2) there exists an embedding  :
: ![W\to\mathbb{R}^{n+k}\times[0,1]](/images/math/a/b/1/ab18bc810bf5b65819b8394370060ae0.png) such that for
such that for 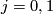 we have
we have
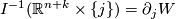 and
and  meets
meets 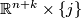 transversally
transversally
3) there exists a vector bundle 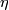 :
: ![E'\to X\times[0,1]](/images/math/8/6/f/86f9e8c19953967e1608f5175d2d4f00.png) of rank
of rank  and for
and for 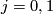 there exist vector bundle isomorphisms
there exist vector bundle isomorphisms 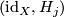 :
: 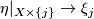
4) there exists a bundle map 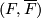 :
: 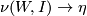 such that for
such that for 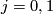 we have
we have 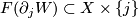 and such that
and such that  :
: ![(W,\partial W)\to(X\times[0,1],X\times\partial[0,1])](/images/math/1/9/5/19515ecbc55dfa41d99b7f8f412e4624.png) has degree one as a map between Poincare pairs.
has degree one as a map between Poincare pairs.
5) for 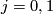 there exist diffeomorphisms
there exist diffeomorphisms 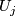 :
: 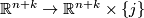 such that
such that
a) 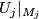 :
: 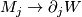 is a diffeomorphism
is a diffeomorphism
b) 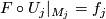
c) the induced bundle map 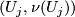 :
: 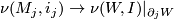 satisfies
satisfies 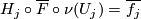 .
.