Petrie conjecture
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Problem
If a compact Lie group  acts smoothly and non-trivially on a closed smooth manifold
acts smoothly and non-trivially on a closed smooth manifold  , what constraints does this place on the topology of
, what constraints does this place on the topology of  in general and on the Pontrjagin classes of
in general and on the Pontrjagin classes of  in particular?
in particular?
In the case where  is homotopy equivalent to
is homotopy equivalent to 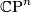 ,
, 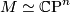 , Petrie [Petrie1972] restricted his attention to smooth actions of the Lie group
, Petrie [Petrie1972] restricted his attention to smooth actions of the Lie group
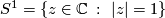 , and posed the following conjecture.
, and posed the following conjecture.
Conjecture 1.1 [Petrie1972].
Suppose that  acts smoothly and non-trivially on a closed smooth
acts smoothly and non-trivially on a closed smooth  -manifold
-manifold 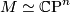 . Then the total Pontrjagin class
. Then the total Pontrjagin class 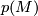 of
of  agrees with that of
agrees with that of 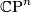 , i.e.,
, i.e.,
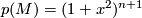 for a generator
for a generator  of
of 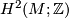 .
.
2 Progress to date
As of November 30, 2010, the Petrie conjecture has not been confirmed in general. However, it has been proven in the following special cases.
- Petrie [Petrie1973] has verified his conjecture under the assumption that the action of
 on
on 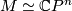 extends to a smooth action of the torus
extends to a smooth action of the torus 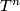 .
.
- By the work of [Dejter1976], the Petrie conjecture is true if
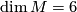 , i.e.,
, i.e., 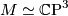 , and more generaly, if
, and more generaly, if 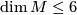 .
.
- According to [Hattori1978], the Petrie conjecture holds if
 admits an invariant almost complex structure with the first Chern class
admits an invariant almost complex structure with the first Chern class 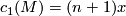 .
.
- Other special cases where the Petrie conjecture holds are described by [Wang1975], [Yoshida1975/76], [Iberkleid1978], and [Muslin1978].
- By [Tsukada&Washiyama1979], [Masuda1981], and [Masuda1983], the Petrie conjecture is true if the fixed point set consists of three or four connected components.
- It follows from [James1985] that the Petrie conjecture is also true if
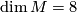 , i.e.,
, i.e., 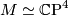 .
.
- The work of [Dessai2002] confirms the Petrie conjecture if the action of
 on
on  extends to an appropriate nice action of
extends to an appropriate nice action of 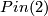 and
and 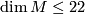 .
.
- According to [Dessai&Wilking2004], the Petrie conjecture holds if the action of
 on
on  extends to a smooth action of the torus
extends to a smooth action of the torus 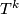 and
and 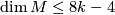 .
.
3 Further discussion
A symplectic version of the Petrie conjecture is discussed in the article of [Tolman2010].
4 References
- [Dejter1976] I. J. Dejter, Smooth
 -manifolds in the homotopy type of
-manifolds in the homotopy type of 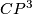 , Michigan Math. J. 23 (1976), no.1, 83–95. MR0402789 (53 #6603) Zbl 0326.57009
, Michigan Math. J. 23 (1976), no.1, 83–95. MR0402789 (53 #6603) Zbl 0326.57009
- [Dessai&Wilking2004] A. Dessai and B. Wilking, Torus actions on homotopy complex projective spaces, Math. Z. 247 (2004), no.3, 505–511. MR2114425 (2006c:57033) Zbl 1068.57034
- [Dessai2002] A. Dessai, Homotopy complex projective spaces with
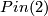 -action, Topology Appl. 122 (2002), no.3, 487–499. MR1911696 (2003f:58048) Zbl 0998.57048
-action, Topology Appl. 122 (2002), no.3, 487–499. MR1911696 (2003f:58048) Zbl 0998.57048
- [Hattori1978] A. Hattori,
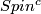 -structures and
-structures and  -actions, Invent. Math. 48 (1978), no.1, 7–31. MR508087 (80e:57051) Zbl 0395.57020
-actions, Invent. Math. 48 (1978), no.1, 7–31. MR508087 (80e:57051) Zbl 0395.57020
- [Iberkleid1978] W. Iberkleid, Pseudolinear spheres, Michigan Math. J. 25 (1978), no.3, 359–370. MR512906 (80d:57023) Zbl 0377.57008
- [James1985] D. M. James, Smooth
 actions on homotopy
actions on homotopy 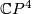 's, Michigan Math. J. 32 (1985), no.3, 259–266. MR803831 (87c:57031) Zbl 0602.57026
's, Michigan Math. J. 32 (1985), no.3, 259–266. MR803831 (87c:57031) Zbl 0602.57026
- [Masuda1981] M. Masuda, On smooth
 -actions on cohomology complex projective spaces. The case where the fixed point set consists of four connected components, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 28 (1981), no.1, 127–167. MR617869 (82i:57031) Zbl 0462.57019
-actions on cohomology complex projective spaces. The case where the fixed point set consists of four connected components, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 28 (1981), no.1, 127–167. MR617869 (82i:57031) Zbl 0462.57019
- [Masuda1983] M. Masuda, Integral weight system of torus actions on cohomology complex projective spaces, Japan. J. Math. (N.S.) 9 (1983), no.1, 55–86. MR722536 (84m:57027) Zbl 0531.57037
- [Muslin1978] Template:Muslin1978
- [Petrie1972] T. Petrie, Smooth
 -actions on homotopy complex projective spaces and related topics, Bull. Amer. Math. Soc. 78 (1972), 105–153. MR0296970 Zbl 0247.57010
-actions on homotopy complex projective spaces and related topics, Bull. Amer. Math. Soc. 78 (1972), 105–153. MR0296970 Zbl 0247.57010
- [Petrie1973] T. Petrie, Torus actions on homotopy complex projective spaces, Invent. Math. 20 (1973), 139–146. MR0322893 (48 #1254) Zbl 0262.57021
- [Tolman2010] S. Tolman, On a symplectic generalization of Petrie's conjecture, Trans. Amer. Math. Soc. 362 (2010), no.8, 3963–3996. MR2638879 Zbl 1216.53074
- [Tsukada&Washiyama1979] E. Tsukada and R. Washiyama,
 -actions on cohomology complex projective spaces with three components of the fixed point sets, Hiroshima Math. J. 9 (1979), no.1, 41–46. MR529325 (80j:57043) Zbl 0411.57037
-actions on cohomology complex projective spaces with three components of the fixed point sets, Hiroshima Math. J. 9 (1979), no.1, 41–46. MR529325 (80j:57043) Zbl 0411.57037
- [Wang1975] K. Wang, Differentiable circle group actions on homotopy complex projective spaces, Math. Ann. 214 (1975), 73–80. MR0372895 (51 #9099) Zbl 0285.57025
- [Yoshida1975/76] T. Yoshida, On smooth semifree
 actions on cohomology complex projective spaces, Publ. Res. Inst. Math. Sci. 11 (1975/76), no.2, 483–496. MR0445528 (56 #3868) Zbl 0326.57008
actions on cohomology complex projective spaces, Publ. Res. Inst. Math. Sci. 11 (1975/76), no.2, 483–496. MR0445528 (56 #3868) Zbl 0326.57008