Grassmann manifolds
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Grassmann manifolds are named after Hermann Grassmann, a German school teacher in Stettin who developed basic notions of linear algebra. They play a key role in topology and geometry as the universal spaces of vector bundles. See also Grassmannian
2 Construction and examples
Let 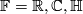 be the real, complex or quaternion field and
be the real, complex or quaternion field and  a vector space over
a vector space over 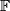 of dimension
of dimension  and let
and let  . A Grassmann manifolds of
. A Grassmann manifolds of  -dimensional subspaces is a set
-dimensional subspaces is a set 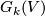 of
of  -dimensional subspaces. The set
-dimensional subspaces. The set 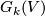 is a quotient of a subset of
is a quotient of a subset of  consisting of linearly independent
consisting of linearly independent  -tuples of vectors with the subspace topology. We define topology on
-tuples of vectors with the subspace topology. We define topology on 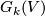 as the quotient topology.
as the quotient topology.
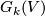 is a Hausdorff, compact space.
is a Hausdorff, compact space. 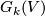 is a connected, compact smooth manifold of dimension
is a connected, compact smooth manifold of dimension 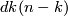 . For
. For 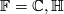 it is also a complex manifold.
it is also a complex manifold.Note that the Grassmann manifold 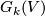 around
around  is locally modelled on the vector space
is locally modelled on the vector space 
Grassmann manifold is a homogeneous space of the general linear group. General linear group 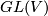 acts transitively on
acts transitively on 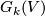 with an isotropy group consisting of automorphisms preserving a given subspace. If the space
with an isotropy group consisting of automorphisms preserving a given subspace. If the space  is equipped with a scalar product (hermitian metric resp.) then the group of isometries
is equipped with a scalar product (hermitian metric resp.) then the group of isometries 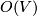 acts transitively and the isotropy group of
acts transitively and the isotropy group of  is
is 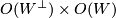 .
.
The Grassmann manifold is equipped with the canonical, tautological vector bundle 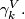 which is a subbundle of the trivial bundle
which is a subbundle of the trivial bundle 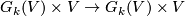 . The total space is
. The total space is 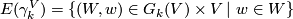 The total space of the associated principal bundle is a Stiefel manifold.
The total space of the associated principal bundle is a Stiefel manifold.
The tangent bundle to Grassmaniann can be expressed in terms of the canonical bundle: 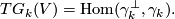
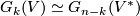 .
. The Grassmannians 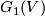 are projective spaces, denoted
are projective spaces, denoted 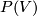 . Note that
. Note that 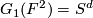 , where
, where 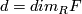 . If we identify
. If we identify 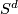 with the one-point compactification of
with the one-point compactification of 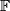 the projection of the canonical principal bundle corresponds to the map
the projection of the canonical principal bundle corresponds to the map 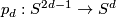 given by
given by  where
where 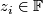 . Note, that the same formula works for octonions
. Note, that the same formula works for octonions 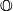 , however the higher dimensional projective spaces over octonions do not exist. The maps
, however the higher dimensional projective spaces over octonions do not exist. The maps 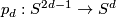 for
for 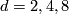 are called the Hopf maps and they play a very important role in homotopy theory; a fibre of
are called the Hopf maps and they play a very important role in homotopy theory; a fibre of 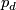 is a sphere
is a sphere 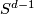 .
.
There is an embedding of the Grassmannian 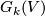 in the Cartesian space
in the Cartesian space 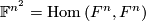 which assigns to every subspace the orthogonal projection on it. If
which assigns to every subspace the orthogonal projection on it. If  is equipped with a norm, the embedding defines a natural (operator) metric on
is equipped with a norm, the embedding defines a natural (operator) metric on 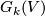 .
.
Infinite dimensional Grassmannians. Natural inclusions of vector space 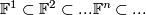 defines inclusions of Grassmannians. The colimit of the resulting sequence is denoted
defines inclusions of Grassmannians. The colimit of the resulting sequence is denoted 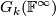 and also
and also 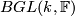 . One can also take the colimit with respect to both dimension of the space and of the subspaces. We have a sequence of inclusions
. One can also take the colimit with respect to both dimension of the space and of the subspaces. We have a sequence of inclusions 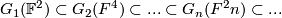 and its colimit is denoted
and its colimit is denoted 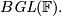
Invariants
Homotopy groups of Grassmannians are closely related to homotopy groups of spheres via the appropriate fibration sequences. They also imply that the groups 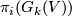 do not depend on
do not depend on  , if
, if 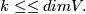 Homotopy groups in the stable range are described by the Bott periodicity theorem.
Homotopy groups in the stable range are described by the Bott periodicity theorem.
Proposition 4.1 {(R.Bott).} For each 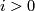 there are isomorphisms:
there are isomorphisms: 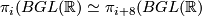 and
and 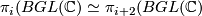
Cohomology groups.
...
3 Classification/Characterization
...
4 Further discussion
Grassmann manifolds are examples of coadjoint orbits [Kirillov2004].
5 References
- [Kirillov2004] A. A. Kirillov, Lectures on the orbit method, Graduate Studies in Mathematics 64, American Mathematical Society, Providence, RI, 2004. MR2069175 (2005c:22001) Zbl 02121486
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
6 External links
- The Wikipedia page on Grassmannian