6-manifolds: 1-connected
|
The user responsible for this page is Alexey Zhubr. No other user may edit this page at present. |
1 Introduction
Let 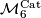 be the set of
be the set of  isomorphism classes of closed oriented simply connected 6-dimensional
isomorphism classes of closed oriented simply connected 6-dimensional  -manifolds, where
-manifolds, where  stands for
stands for 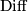 (smooth manifolds),
(smooth manifolds), 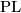 (piecewise linear manifolds) or
(piecewise linear manifolds) or 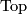 (topological manifolds). On this page we describe the results of calculation of the sets
(topological manifolds). On this page we describe the results of calculation of the sets 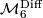 and
and 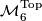 begun by [Smale1962], extended in [Wall1966], [Jupp1973] and [Zhubr1975], and finally completed in [Zhubr2000]. An excellent summary for the torsion-free case (for those
begun by [Smale1962], extended in [Wall1966], [Jupp1973] and [Zhubr1975], and finally completed in [Zhubr2000]. An excellent summary for the torsion-free case (for those 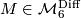 with
with 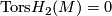 ) may be found in [Okonek&Van de Ven1995, Section 1]. For the case
) may be found in [Okonek&Van de Ven1995, Section 1]. For the case 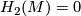 see 6-manifolds:2-connected.
see 6-manifolds:2-connected.
Remark 1.1.
- The sets
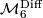 and
and 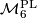 are actually the same (as Wall points out in [Wall1966]): by Whitehead triangulation theorem we have the canonical forgetting map
are actually the same (as Wall points out in [Wall1966]): by Whitehead triangulation theorem we have the canonical forgetting map 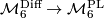 ; by smoothing theory and the fact that
; by smoothing theory and the fact that 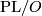 is
is  -connected, this is a bijection.
-connected, this is a bijection. - The forgetting map
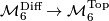 is injective: this follows from classification results below. Thus
is injective: this follows from classification results below. Thus 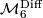 can be viewed as a subset of
can be viewed as a subset of 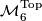 (determined by the equation
(determined by the equation 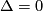 , where
, where  is the Kirby-Siebenmann triangulation class). In what follows, we abbreviate
is the Kirby-Siebenmann triangulation class). In what follows, we abbreviate  to just
to just  .
.
2 Classification
2.1 Notation
The standard projections 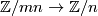 are denoted by
are denoted by 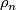 , the standard injections
, the standard injections 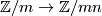 by
by 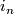 (here
(here  may equal
may equal  , in which case
, in which case 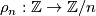 is the reduction modulo
is the reduction modulo  , while
, while 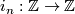 is the multiplication by
is the multiplication by  ). By
). By  we denote the (non-stable) cohomology operation ``Pontrjagin square´´
we denote the (non-stable) cohomology operation ``Pontrjagin square´´
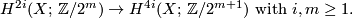
It is known that (with the same  ) the following equalities hold:
) the following equalities hold: 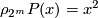 and
and 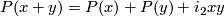 . There exists also the ``Pontrjagin cube´´
. There exists also the ``Pontrjagin cube´´
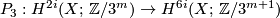
and generally the ``Pontrjagin  -th power´´ for every prime
-th power´´ for every prime  [Thomas1956] (here we only need
[Thomas1956] (here we only need 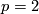 and
and 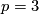 ).
).
2.2 Classical invariants
Let  be a closed oriented simply connected 6-manifold (
be a closed oriented simply connected 6-manifold (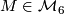 for short). Our first two invariants determine the (additive) homology structure of
for short). Our first two invariants determine the (additive) homology structure of  :
:
-
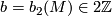 - the 3-dimensional Betty number,
- the 3-dimensional Betty number,
-
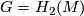 - the 2-dimensional homology group.
- the 2-dimensional homology group.
Next, we consider the characteristic classes:
-
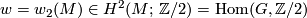 - the second Stiefel-Whitney class;
- the second Stiefel-Whitney class;
-
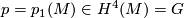 - the first Pontrjagin class (in view of Poincaré duality, we will freely use such identifications as
- the first Pontrjagin class (in view of Poincaré duality, we will freely use such identifications as 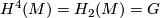 etc.);
etc.);
-
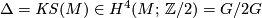 -the Kirby-Siebenmann class (obstruction to smoothing the
-the Kirby-Siebenmann class (obstruction to smoothing the 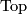 -manifold
-manifold  ).
).
Note that all the other Stiefel-Whitney classes are uniquely determined as 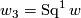 ,
, 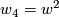 by the well-known Wu formulas and
by the well-known Wu formulas and  by trivial reasons. Also, the class
by trivial reasons. Also, the class 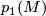 may need some comment. In general, Pontrjagin classes for
may need some comment. In general, Pontrjagin classes for 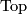 manifolds (or
manifolds (or 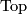 microbundles) are defined as rational cohomology classes. The class
microbundles) are defined as rational cohomology classes. The class 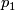 is an exception, due to the equality
is an exception, due to the equality 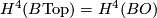 , see [Jupp1973] or [Kirby&Siebenmann1977]. We denote by
, see [Jupp1973] or [Kirby&Siebenmann1977]. We denote by 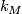 the canonical mapping (or rather homotopy class of mappings)
the canonical mapping (or rather homotopy class of mappings) 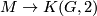 , inducing the identity
, inducing the identity 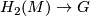 . Now, the last invariant
. Now, the last invariant
-
![\mu=(k_M)_*[M]\in H_6(G,2)](/images/math/3/9/9/399921d931a6092f48c317af0e75aa0a.png) ,
,
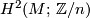 for every
for every  . First, the class
. First, the class  determines the family of trilinear functions
determines the family of trilinear functions 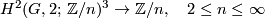
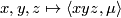 ; note that
; note that 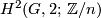 is the same as
is the same as 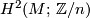 . In what follows, instead of
. In what follows, instead of 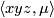 we may write
we may write ![\langle xyz,[M]\rangle](/images/math/e/e/6/ee69a0045dea68d122a89ed53b64b685.png) or sometimes simply
or sometimes simply 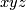 . Second, there are two more families:
. Second, there are two more families: 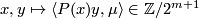
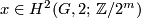 ,
, 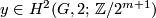 , and
, and 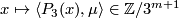
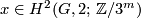 . From the structure of the groups
. From the structure of the groups 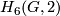 one can easily deduce that, conversely,
one can easily deduce that, conversely,  is uniquely determined by all these values.
is uniquely determined by all these values.
2.3 Relations for classical invariants
There are two evident restrictions for invariants  and
and  :
:
-
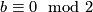 ;
;
-
 is a finitely generated abelian group
is a finitely generated abelian group
(where the first one follows from the existence of non-singular skew-symmetric form on 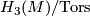 ). There are two more restrictions (Wu relations):
). There are two more restrictions (Wu relations):
- (
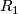 )
) 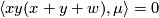 for all
for all 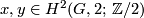 ,
,
- (
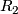 )
) 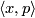 =
=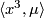 for all
for all 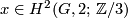 .
.
These relations are given in [Wall1966, Theorem 3]. Wall formulates them for torsion-free case and in integral form (and for smooth category), but the argument for general case is the same. We call them ``Wu relations´´ because (as Wall points out) they are easily deduced from the well-known Wu formula ![\langle (\mathrm{Sq}+v)x,[M] \rangle =0](/images/math/2/e/d/2ed1aadb9f05727e5530b7df325c359f.png) for
for 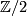 -coefficients, and its certain analogue for
-coefficients, and its certain analogue for 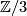 . Note that (
. Note that (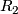 ) could be also written as
) could be also written as 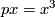 , having in mind multiplication ``on
, having in mind multiplication ``on  ´´.
´´.
2.4 Further notation
 ,
,  , we denote by
, we denote by 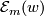 the set of all
the set of all 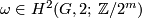 satisfying
satisfying 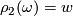 . Note that
. Note that 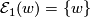 , and that
, and that 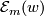 may become empty for
may become empty for  sufficiently large. We write
sufficiently large. We write 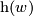 for
for 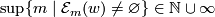 . Let
. Let  be any integer in
be any integer in 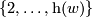 . For any
. For any 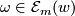 and any
and any 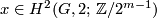 , and assuming relation (
, and assuming relation (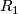 ) satisfied, we have
) satisfied, we have 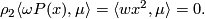
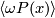 is in the image of the inclusion
is in the image of the inclusion 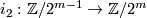 , and we set
, and we set 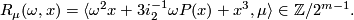
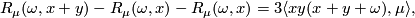
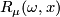 is linear in
is linear in  for
for 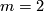 (by (
(by (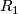 ) again).
) again).
2.5 Special invariants
There is a detailed treatment in [Zhubr2000]. Here we only give a formal description. For each 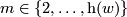 there are functions
there are functions
-
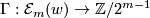 ,
,
-
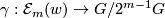 .
.
In what follows, the values of 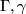 at
at 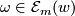 will be written either
will be written either 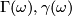 or
or 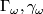 , depending on convenience. These functions satisfy the following set of identities (which are considered to be part of the definition, whereas the relations define the range):
, depending on convenience. These functions satisfy the following set of identities (which are considered to be part of the definition, whereas the relations define the range):
- [
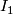 ]
] 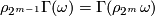 (first coefficient formula),
(first coefficient formula),
- [
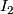 ]
] 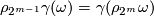 (second coefficient formula)
(second coefficient formula)
for 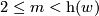 , and
, and
- [
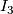 ]
] 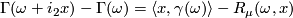 (first difference formula),
(first difference formula),
- [
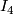 ]
] 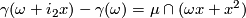 (second difference formula)
(second difference formula)
for 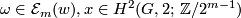 .
.
Remark 2.1.
- In view of these identities, one easily sees that the functions
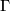 and
and 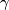 are completely determined by their values at some fixed
are completely determined by their values at some fixed 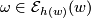 . Thus, if we could make a canonical choice, then our couple of invariants would trivialize to just
. Thus, if we could make a canonical choice, then our couple of invariants would trivialize to just 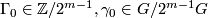 . Evidently, such canonical choice is impossible in general, however in the spin case one can take
. Evidently, such canonical choice is impossible in general, however in the spin case one can take 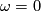 (with
(with  ).
). - From (
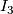 ) it easily follows that
) it easily follows that 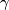 is in fact determined by
is in fact determined by 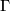 , so our list of invariants could be reduced by 1, at the cost of reduced convenience.
, so our list of invariants could be reduced by 1, at the cost of reduced convenience.
2.6 Relations for special invariants
- (
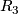 )
) 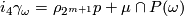 for
for 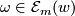 ,
,
- (
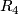 )
) 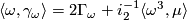 for
for 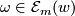 ,
,
- (
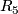 )
) 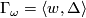 for
for 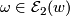 .
.
2.7 The splitting theorem
Wall in [Wall1966] proves the following
Theorem 2.2.
Let  be a closed, smooth, 1-connected 6-manifold. Then we can write
be a closed, smooth, 1-connected 6-manifold. Then we can write  as a connected sum
as a connected sum 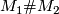 , where
, where 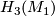 is finite and
is finite and 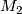 is a connected sum of copies of
is a connected sum of copies of 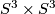 .
.
This theorem allows to restrict the classification problem to the case where 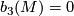 . The proof is rather easy and basically reduces to realizing the standard ``symplectic´´ basis of
. The proof is rather easy and basically reduces to realizing the standard ``symplectic´´ basis of 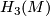 with embedded 3-spheres (and applying ``Whitney trick´´ where necessary). As is pointed out in [Jupp1973], the same argument works for
with embedded 3-spheres (and applying ``Whitney trick´´ where necessary). As is pointed out in [Jupp1973], the same argument works for 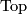 category. Note that Wall does not state the uniqueness of
category. Note that Wall does not state the uniqueness of  in this theorem, however uniqueness follows from his classification theorem [Wall1966, Theorem 5] for smooth, spin, torsion-free manifolds. Likewize, uniqueness of the above splitting follows for all torsion-free manifolds (both in
in this theorem, however uniqueness follows from his classification theorem [Wall1966, Theorem 5] for smooth, spin, torsion-free manifolds. Likewize, uniqueness of the above splitting follows for all torsion-free manifolds (both in 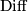 and
and 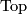 ) from the results of [Jupp1973], and in full generality from the general classification theorem of [Zhubr2000] (see below). Note that the invariants (except
) from the results of [Jupp1973], and in full generality from the general classification theorem of [Zhubr2000] (see below). Note that the invariants (except  of course) are ``insensitive´´ to connected summing with
of course) are ``insensitive´´ to connected summing with 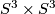 (this is evident for classical invariants, while for
(this is evident for classical invariants, while for 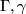 we refer to their definition in [Zhubr2000]). It should be also noted that the uniqueness statement for Theorem 2.2 was proved directly (independent of classification) in [Zhubr1973].
we refer to their definition in [Zhubr2000]). It should be also noted that the uniqueness statement for Theorem 2.2 was proved directly (independent of classification) in [Zhubr1973].
2.8 Functorial behaviour of invariants
Consider the set of invariants  ,
,  ,
,  ,
, 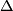 ,
,  ,
, 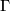 ,
, 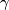 (with
(with  left out). We divide these into two subsets:
left out). We divide these into two subsets: 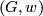 and
and 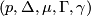 . We say that the set
. We say that the set 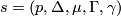 is admissible for
is admissible for 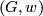 if
if 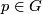 ,
, 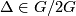 etc. satisfy all the identities and relations given above (these invariants are now regarded in ``abstract´´ way, irrelative to any manifold). Let
etc. satisfy all the identities and relations given above (these invariants are now regarded in ``abstract´´ way, irrelative to any manifold). Let 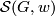 denote the collection of all admissible sets of invariants for
denote the collection of all admissible sets of invariants for 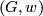 . Consider now the category
. Consider now the category 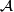 of finitely generated abelian groups, and the category
of finitely generated abelian groups, and the category 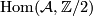 , whose objects are homomorphisms
, whose objects are homomorphisms 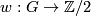 with
with 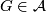 , and whose morphisms are commutative diagrams of the form
, and whose morphisms are commutative diagrams of the form
![\displaystyle \xymatrix{G\ar[rr]\ar[dr]^w && G'\ar[dl]_{w'} \\ & \Zz/2}](/images/math/f/7/3/f73f60e0a43b3886d5b85edb6c4865e7.png)
For each morphism 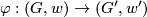 , we can define the induced map
, we can define the induced map 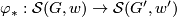 in a natural way: if
in a natural way: if 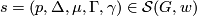 , then we set
, then we set 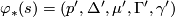 with
with 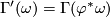 and
and 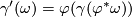 (the rest is quite evident). One easily verifies that the new invariant set is admissible again. Hence we have a functor
(the rest is quite evident). One easily verifies that the new invariant set is admissible again. Hence we have a functor 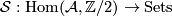 .
.
2.9 Classification theorem (the general case)
We use the notation 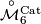 for the subset of
for the subset of 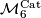 , determined by the equation
, determined by the equation 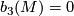 . For any
. For any 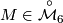 and
and 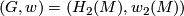 , let
, let 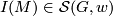 be the set
be the set 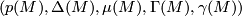 . The following theorem [Zhubr2000], Theorem 6.3] gives the topological and differential classification of all closed oriented simply connected 6-manifolds.
. The following theorem [Zhubr2000], Theorem 6.3] gives the topological and differential classification of all closed oriented simply connected 6-manifolds.
Theorem 2.3.
(1) Let 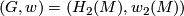 and
and 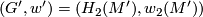 , where
, where 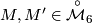 . An isomorphism
. An isomorphism 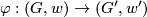 is induced by orientation-preserving homeomorphism
is induced by orientation-preserving homeomorphism 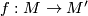 if and only if
if and only if 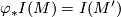 (completeness of the set of invariants). (2) For each
(completeness of the set of invariants). (2) For each 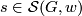 there exists
there exists 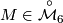 with
with 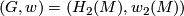 and
and 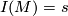 (completeness of the set of relations). (3) If manifolds
(completeness of the set of relations). (3) If manifolds  and
and 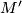 (statement (1)) are provided with smooth structures, then homeomorphism
(statement (1)) are provided with smooth structures, then homeomorphism  can be chosen smooth.
can be chosen smooth.
Remark 2.4.
- The clause "only if" of the statement (1) is tautological (it just says that our invariants are invariants indeed).
- For any
 let
let 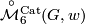 denote the set of
denote the set of  -isomorphism classes of pairs
-isomorphism classes of pairs 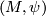 , where
, where 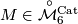 and
and 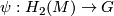 is an isomorphism with
is an isomorphism with 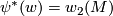 . One can say that
. One can say that 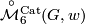 is the set of (isomorphism classes of) manifolds with prescribed 2-dimensional homology group and second Stiefel-Whitney class. We can write (taking some liberty in notations): Now we have the natural maps
is the set of (isomorphism classes of) manifolds with prescribed 2-dimensional homology group and second Stiefel-Whitney class. We can write (taking some liberty in notations): Now we have the natural maps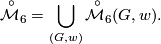
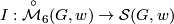 , and from the above theorem it follows that all these maps are bijections.
, and from the above theorem it follows that all these maps are bijections. - From the statement (3) it evidently follows that a closed simply connected 6-manifold has at most one (up to homeomorphism) smooth structure (Hauptvermutung).
2.10 The spin case
...
2.11 The torsion-free case
...
3 Examples and constructions
We first present some familiar 6-manifolds.
-
 , the 6-sphere.
, the 6-sphere.
-
 , the
, the  -fold connected sum of
-fold connected sum of 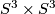 .
.
-
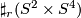 , the
, the  -fold connected sum of
-fold connected sum of 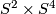 .
.
-
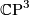 , 3-dimensional complex projective space.
, 3-dimensional complex projective space.
-
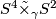 , the non-trivial linear 4-sphere bundle over
, the non-trivial linear 4-sphere bundle over  .
.
- For each
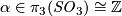 we have
we have 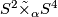 , the corresponding 2-sphere bundle over
, the corresponding 2-sphere bundle over  . If we write 1 for a generator of
. If we write 1 for a generator of 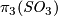 then
then 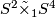 is diffeomorphic to
is diffeomorphic to 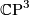 .
.
- The smooth manifold underlying any 1-connected complex manifold of dimension 3 is a 1-connected 6-manifold:
- in particular, every complete intersection of complex dimension 3 is a 1-connected 6-manifold.
- Let
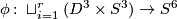 be an
be an  -component framed link and let denote by
-component framed link and let denote by 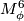 the outcome of surgery on
the outcome of surgery on  . Then
. Then 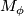 is a simply connected spinable 6-manifold with
is a simply connected spinable 6-manifold with 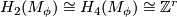 and
and 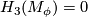 .
.
4 References
- [Jupp1973] P. E. Jupp, Classification of certain
 -manifolds, Proc. Cambridge Philos. Soc. 73 (1973), 293–300. MR0314074 (47 #2626) Zbl 0249.57005
-manifolds, Proc. Cambridge Philos. Soc. 73 (1973), 293–300. MR0314074 (47 #2626) Zbl 0249.57005
- [Kirby&Siebenmann1977] R. C. Kirby and L. C. Siebenmann, Foundational essays on topological manifolds, smoothings, and triangulations, Princeton University Press, Princeton, N.J., 1977. MR0645390 (58 #31082) Zbl 0361.57004
- [Okonek&Van de Ven1995] C. Okonek and A. Van de Ven, Cubic forms and complex
 -folds, Enseign. Math. (2) 41 (1995), no.3-4, 297–333. MR1365849 (97b:32035) Zbl 0869.14018
-folds, Enseign. Math. (2) 41 (1995), no.3-4, 297–333. MR1365849 (97b:32035) Zbl 0869.14018
- [Smale1962] S. Smale, On the structure of
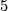 -manifolds, Ann. of Math. (2) 75 (1962), 38–46. MR0141133 (25 #4544) Zbl 0101.16103
-manifolds, Ann. of Math. (2) 75 (1962), 38–46. MR0141133 (25 #4544) Zbl 0101.16103
- [Thomas1956] E. Thomas, A generalization of the Pontrjagin square cohomology operation, Proc. Nat. Acad. Sci. U.S.A. 42 (1956), 266–269. MR0079254 (18,57b) Zbl 0071.16302
- [Wall1966] C. T. C. Wall, Classification problems in differential topology. V. On certain
 -manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601
-manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601
- [Zhubr1973] A. V. Zhubr, A decomposition theorem for simply connected 6-manifolds, LOMI seminar notes 36 (1973), 40–49. (Russian)
- [Zhubr1975] A. V. Zhubr, Classification of simply connected six-dimensional spinor manifolds, (English) Math. USSR, Izv. 9 (1975), (1976), 793–812 . Zbl 0337.57004
- [Zhubr2000] A. V. Zhubr, Closed simply connected six-dimensional manifolds: proofs of classification theorems, Algebra i Analiz 12 (2000), no.4, 126–230. MR1793619 (2001j:57041)