Normal maps and submanifolds (Ex)
From Manifold Atlas
Revision as of 13:53, 1 April 2012 by Diarmuid Crowley (Talk | contribs)
Let 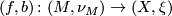 be a degree one normal map. For simplicity, assume that
be a degree one normal map. For simplicity, assume that  and
and  are closed oriented
are closed oriented 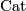 -manifolds of dimension
-manifolds of dimension  . Suppose that
. Suppose that  is a codimension
is a codimension  oriented submanifold
oriented submanifold  with normal bundle
with normal bundle 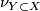 and that that
and that that  is transverse to
is transverse to  . Prove the following:
. Prove the following:
- There is a canonical degree one normal map
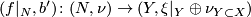 .
.
- This defines a well-defined map
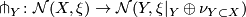 .
.
Of course we have the surgery obstruction map
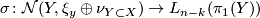
and the composite map
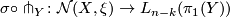
which is called the splitting obstruction map along  . In addition prove the following:
. In addition prove the following:
- If
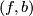 is normally bordant to a homeomorphism then the splitting obstruction along
is normally bordant to a homeomorphism then the splitting obstruction along  vanishes.
vanishes.