Quadratic forms for surgery
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Let 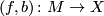 be a degree one normal map from a manifold of dimension
be a degree one normal map from a manifold of dimension 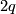 . Then the surgery kernel of
. Then the surgery kernel of 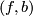 ,
, 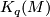 , comes equipped with a subtle and crucial quadratic refinement. This page describes both the algebraic and geometric aspects of such quadratic refinements
, comes equipped with a subtle and crucial quadratic refinement. This page describes both the algebraic and geometric aspects of such quadratic refinements
2 Topology
2.1 The 4k+2 dimensional case
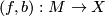
 -connected normal map,
-connected normal map, 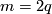 ,
,  odd and
odd and 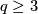 . Assume also
. Assume also  is
is  -connected. Let
-connected. Let 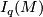
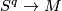 which represent elements of the surgery kernel
which represent elements of the surgery kernel 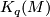 (with respect to the homomorphism
(with respect to the homomorphism 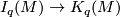 .
.
It is an abelian group using the connected summ operation (this uses the condition 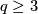 ).
).
Then we have three invariants:
-
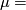 double point obstruction
double point obstruction 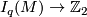 ,
,
-
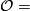 Browder's framing obstruction
Browder's framing obstruction 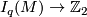 , and
, and
-
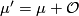 .
.
1 Definition of the framing obstruction
Each element of 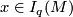 is represented by a commutative square
is represented by a commutative square
![\displaystyle \SelectTips{cm}{} \xymatrix{ S^q \ar[r]^\phi \ar[d] & M \ar[d]^{f}\\ D^{q+1} \ar[r] & X }](/images/math/6/5/4/6547c00a0ee15554d7bc5cf41ae3a917.png)
with  an immersion, and a diagram of normal bundle data
an immersion, and a diagram of normal bundle data
![\displaystyle \SelectTips{cm}{} \xymatrix{ S^q \ar[r]^{\nu_\phi} \ar[d] & B\text{O}_q \ar[d]^{f}\\ D^{q+1} \ar[r] & B\text{O} }](/images/math/1/4/d/14dcd20fe881205d067d6a82b1af71df.png)
the latter defining a stable trivialization of the normal bundle of  .
The homotopy class of the latter diagram defines an element of
.
The homotopy class of the latter diagram defines an element of 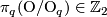 . This element
defines
. This element
defines 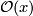 .
.
2 Definition of the self-intersection obstruction
A generic immersion 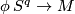 has only double points with transverse crossings. Then
has only double points with transverse crossings. Then ![\mu([\phi]) \in {\Bbb Z}_2](/images/math/9/2/b/92bca1727cdffd74905d92aa4f801649.png) is defined to be the number
of double points of
is defined to be the number
of double points of  taken modulo two. This only depends on
taken modulo two. This only depends on ![[\phi]=](/images/math/8/6/d/86dfdb8336ab311285b59d76a393c9cf.png) the regular homotopy class of
the regular homotopy class of  .
.
Note that
 is a quadratic function, i.e.,
is a quadratic function, i.e.,
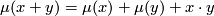
where  denotes the intersection pairing applied to
denotes the intersection pairing applied to  and
and  considered as elements of
considered as elements of 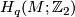 .
.
3 Homotopy Invariance
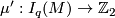
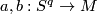 are immersions representing the same element
are immersions representing the same element 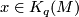 , then
, then 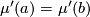 ).
).
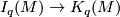 is onto and two-to-one. The distinct elements over a given
is onto and two-to-one. The distinct elements over a given 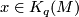 are detected by Browder's framing obstruction
are detected by Browder's framing obstruction 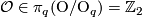
(this uses Smale-Hirsch theory).
Let  and
and  be immersions representing these elements. Then
be immersions representing these elements. Then  and
and  are not regularly homotopic. (Note: when
are not regularly homotopic. (Note: when 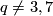 the normal bundles of
the normal bundles of  and
and  are distinct; when
are distinct; when 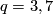 they are both trivial.) We can assume without loss in generality that
they are both trivial.) We can assume without loss in generality that 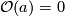 (so
(so 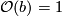 ). Then
). Then  is a framed immersion.
is a framed immersion.
- Case 1:
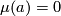 .
.
If 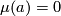 then a result of Whitney (the "Whitney trick") shows that
then a result of Whitney (the "Whitney trick") shows that  is regularly homotopic to a (framed) embedding, so assume that
is regularly homotopic to a (framed) embedding, so assume that  is a framed embedding. Whitney's method of introducing a single double point to
is a framed embedding. Whitney's method of introducing a single double point to  in a coordinate chart yields a new immersion
in a coordinate chart yields a new immersion 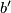 such that
such that 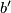 has one double point and
has one double point and 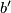 still represents
still represents  . Then
. Then 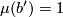 , so
, so 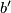 isn't regularly homotopic to
isn't regularly homotopic to  . It must therefore be regularly homotopic to
. It must therefore be regularly homotopic to  . Hence
. Hence 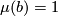 . It follows that
. It follows that 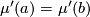 in this case.
in this case.
- Case 2:
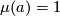 .
.
In this case  is regularly homotopic to an immersion with exactly one double point. By introducing another double point we get a
is regularly homotopic to an immersion with exactly one double point. By introducing another double point we get a 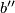 representing
representing  such that
such that 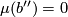 . Then
. Then 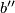 is not regularly homotopic to
is not regularly homotopic to  so it must be regularly homotopic to
so it must be regularly homotopic to  . Consequently,
. Consequently, 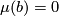 . Therefore
. Therefore 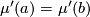 in this case.
in this case.
Let 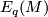 denote the isotopy classes of embeddings
denote the isotopy classes of embeddings 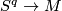 representing elements of
representing elements of 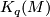 . Then we have a function
. Then we have a function 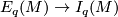 .
.
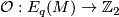 factors through
factors through 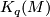 .
. 3 Algebra
4 References
$-connected. Let $$I_q(M)$$ be the set of regular homotopy classes of immersions $S^q \to M$ which represent elements of the surgery kernel $K_q(M)$ (with respect to the homomorphism $I_q(M) \to K_q(M)$. It is an abelian group using the connected summ operation (this uses the condition $q \ge 3$). Then we have three invariants: * $\mu =$ double point obstruction $I_q(M) \to \Bbb Z_2$, * ${\mathcal O} =$ Browder's framing obstruction $I_q(M) \to \Bbb Z_2$, and * $\mu' = \mu + {\mathcal O}$. ====Definition of the framing obstruction==== Each element of $x\in I_q(M)$ is represented by a commutative square $$ \SelectTips{cm}{} \xymatrix{ S^q \ar[r]^\phi \ar[d] & M \ar[d]^{f}\ D^{q+1} \ar[r] & X } $$ with $\phi$ an immersion, and a diagram of normal bundle data $$ \SelectTips{cm}{} \xymatrix{ S^q \ar[r]^{\nu_\phi} \ar[d] & B\text{O}_q \ar[d]^{f}\ D^{q+1} \ar[r] & B\text{O} } $$ the latter defining a stable trivialization of the normal bundle of $\phi$. The homotopy class of the latter diagram defines an element of $\pi_q(\text{O}/\text{O}_q) \in \Bbb Z_2$. This element defines ${\mathcal O}(x)$. ====Definition of the self-intersection obstruction==== A generic immersion $\phi\: S^q \to M$ has only double points whose crossings are transversal. $\mu([\phi]) \in {\Bbb Z}_2$ is defined to be the number of double points of $\phi$ taken modulo two. This only depends on $[\phi]=$ regular homotopy class of $\phi$. Note that $\mu$ is a ''quadratic function,'' i.e., $$ \mu(x+y) = \mu(x) + \mu(y) + x\cdot y $$ where $x\cdot y$ denotes the intersection pairing applied to $x$ and $y$ considered as elements of $H_q(M;{\Bbb Z}_2)$. ====Homotopy Invariance==== {{beginthm|Theorem}} The function $$ \mu': I_q(M) \to \Bbb Z_2 $$ is homotopy invariant. That is, if $a,b: S^q \to M$ are immersions representing the same element $x \in K_q(M)$, then $\mu'(a) = \mu'(b)$). {{endthm}} '''Proof:''' The homomorphism $I_q(M) \to K_q(M)$ is onto and two-to-one. The distinct elements over a given $x \in K_q(M)$ are detected by Browder's framing obstruction $${\mathcal O} \in \pi_{q}(\text{O}/\text{O}_q) = \Bbb Z_2$$ (this uses Smale-Hirsch theory). Let $a$ and $b$ be immersions representing these elements. Then $a$ and $b$ are not regularly homotopic. (Note: when $q\ne 3,7$ the normal bundles of $a$ and $b$ are distinct; when $q=3,7$ they are both trivial.) We can assume without loss in generality that ${\mathcal O}(a) = 0$ (so ${\mathcal O}(b) =1$). Then $a$ is a framed immersion. * ''Case 1:'' $\mu(a) = 0$. If $\mu(a) = 0 $ then a result of Whitney (the "Whitney trick") shows that $a$ is regularly homotopic to a (framed) embedding, so assume that $a$ is a framed embedding. Whitney's method of introducing a single double point to $a$ in a coordinate chart yields a new immersion $b'$ such that $b'$ has one double point and $b'$ still represents $x$. Then $\mu(b') = 1$, so $b'$ isn't regularly homotopic to $a$. It must therefore be regularly homotopic to $b$. Hence $\mu(b) = 1$. It follows that $\mu'(a) = \mu'(b)$ in this case. *''Case 2:'' $\mu(a) = 1$. In this case $a$ is regularly homotopic to an immersion with exactly one double point. By introducing another double point we get a $b''$ representing $x$ such that $\mu(b'') = 0$. Then $b''$ is not regularly homotopic to $a$ so it must be regularly homotopic to $b$. Consequently, $\mu(b) = 0$. Therefore $\mu'(a) = \mu'(b)$ in this case.$\Box$ Let $E_q(M)$ denote the isotopy classes of embeddings $S^q \to M$ representing elements of $K_q(M)$. Then we have a function $E_q(M) \to I_q(M)$. {{beginthm|Corollary}} The function ${\mathcal O}: E_q(M) \to \Bbb Z_2$ factors through $K_q(M)$. {{endthm}} == Algebra == == References == {{#RefList:}} [[Category:Theory]](f, b) \colon M \to X be a degree one normal map from a manifold of dimension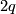 . Then the surgery kernel of
. Then the surgery kernel of 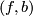 ,
, 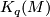 , comes equipped with a subtle and crucial quadratic refinement. This page describes both the algebraic and geometric aspects of such quadratic refinements
, comes equipped with a subtle and crucial quadratic refinement. This page describes both the algebraic and geometric aspects of such quadratic refinements
2 Topology
2.1 The 4k+2 dimensional case
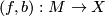
 -connected normal map,
-connected normal map, 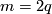 ,
,  odd and
odd and 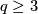 . Assume also
. Assume also  is
is  -connected. Let
-connected. Let 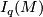
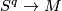 which represent elements of the surgery kernel
which represent elements of the surgery kernel 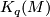 (with respect to the homomorphism
(with respect to the homomorphism 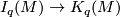 .
.
It is an abelian group using the connected summ operation (this uses the condition 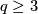 ).
).
Then we have three invariants:
-
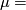 double point obstruction
double point obstruction 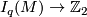 ,
,
-
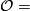 Browder's framing obstruction
Browder's framing obstruction 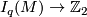 , and
, and
-
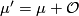 .
.
1 Definition of the framing obstruction
Each element of 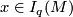 is represented by a commutative square
is represented by a commutative square
![\displaystyle \SelectTips{cm}{} \xymatrix{ S^q \ar[r]^\phi \ar[d] & M \ar[d]^{f}\\ D^{q+1} \ar[r] & X }](/images/math/6/5/4/6547c00a0ee15554d7bc5cf41ae3a917.png)
with  an immersion, and a diagram of normal bundle data
an immersion, and a diagram of normal bundle data
![\displaystyle \SelectTips{cm}{} \xymatrix{ S^q \ar[r]^{\nu_\phi} \ar[d] & B\text{O}_q \ar[d]^{f}\\ D^{q+1} \ar[r] & B\text{O} }](/images/math/1/4/d/14dcd20fe881205d067d6a82b1af71df.png)
the latter defining a stable trivialization of the normal bundle of  .
The homotopy class of the latter diagram defines an element of
.
The homotopy class of the latter diagram defines an element of 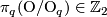 . This element
defines
. This element
defines  .
.
2 Definition of the self-intersection obstruction
A generic immersion 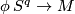 has only double points with transverse crossings. Then
has only double points with transverse crossings. Then ![\mu([\phi]) \in {\Bbb Z}_2](/images/math/9/2/b/92bca1727cdffd74905d92aa4f801649.png) is defined to be the number
of double points of
is defined to be the number
of double points of  taken modulo two. This only depends on
taken modulo two. This only depends on ![[\phi]=](/images/math/8/6/d/86dfdb8336ab311285b59d76a393c9cf.png) the regular homotopy class of
the regular homotopy class of  .
.
Note that
 is a quadratic function, i.e.,
is a quadratic function, i.e.,
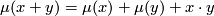
where  denotes the intersection pairing applied to
denotes the intersection pairing applied to  and
and  considered as elements of
considered as elements of 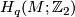 .
.
3 Homotopy Invariance
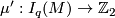
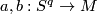 are immersions representing the same element
are immersions representing the same element 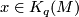 , then
, then 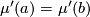 ).
).
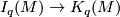 is onto and two-to-one. The distinct elements over a given
is onto and two-to-one. The distinct elements over a given 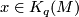 are detected by Browder's framing obstruction
are detected by Browder's framing obstruction 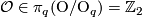
(this uses Smale-Hirsch theory).
Let  and
and  be immersions representing these elements. Then
be immersions representing these elements. Then  and
and  are not regularly homotopic. (Note: when
are not regularly homotopic. (Note: when 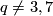 the normal bundles of
the normal bundles of  and
and  are distinct; when
are distinct; when 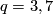 they are both trivial.) We can assume without loss in generality that
they are both trivial.) We can assume without loss in generality that 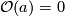 (so
(so 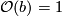 ). Then
). Then  is a framed immersion.
is a framed immersion.
- Case 1:
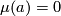 .
.
If 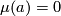 then a result of Whitney (the "Whitney trick") shows that
then a result of Whitney (the "Whitney trick") shows that  is regularly homotopic to a (framed) embedding, so assume that
is regularly homotopic to a (framed) embedding, so assume that  is a framed embedding. Whitney's method of introducing a single double point to
is a framed embedding. Whitney's method of introducing a single double point to  in a coordinate chart yields a new immersion
in a coordinate chart yields a new immersion 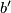 such that
such that 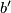 has one double point and
has one double point and 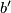 still represents
still represents  . Then
. Then 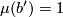 , so
, so 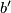 isn't regularly homotopic to
isn't regularly homotopic to  . It must therefore be regularly homotopic to
. It must therefore be regularly homotopic to  . Hence
. Hence 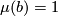 . It follows that
. It follows that 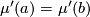 in this case.
in this case.
- Case 2:
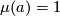 .
.
In this case  is regularly homotopic to an immersion with exactly one double point. By introducing another double point we get a
is regularly homotopic to an immersion with exactly one double point. By introducing another double point we get a 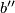 representing
representing  such that
such that 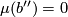 . Then
. Then 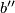 is not regularly homotopic to
is not regularly homotopic to  so it must be regularly homotopic to
so it must be regularly homotopic to  . Consequently,
. Consequently, 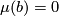 . Therefore
. Therefore 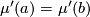 in this case.
in this case.
Let 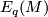 denote the isotopy classes of embeddings
denote the isotopy classes of embeddings 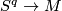 representing elements of
representing elements of 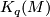 . Then we have a function
. Then we have a function 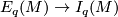 .
.
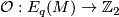 factors through
factors through 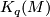 .
.